|
|
#1
\(y^{\prime }\left (x\right )-\frac {1}{\sqrt {a_{4}x^{4}+a_{3}x^{3}+a_{2}x^{2}+a_{1}x+a_{0}}}=0\)
Maple
restart;
ode1:=diff(y(x),x)-(a4*x^4+a3*x^3+a2*x^2+a1*x+a0)^(-1/2)=0;
dsolve(%,y(x));
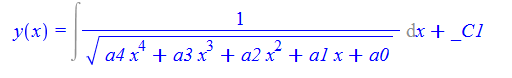
Mathematica
Remove["Global`*"]
ode1=y'[x]-1/Sqrt[(a4 x^4+a3 x^3+a2 x^2+a1 x+a0)]==0;
DSolve[ode1,y,x]

|
|
|
#2
\(y^{\prime }\left ( x\right ) +ay\left ( x\right ) =ce^{bx}\)
Maple
restart;
ode2:=diff(y(x),x)+a*y(x)=c*exp(b*x);
dsolve(%,y(x));
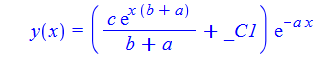
Mathematica
Remove["Global`*"]
ode2=y'[x]+a y[x]-c Exp[b*x]==0
DSolve[%,y[x],x]// TraditionalForm
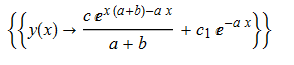
|
|
|
#3
\(y^{\prime }\left ( x\right ) +ay\left ( x\right ) -b\sin \left ( cx\right ) =0\)
Maple
restart;
ode3:=diff(y(x),x)+a*y(x)-b*sin(c*x)=0:
dsolve(%,y(x));
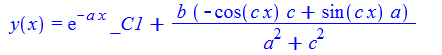
Mathematica
Remove["Global`*"]
ode3=y'[x]+a y[x]-b Sin[c x]==0;
DSolve[%,y[x],x]// TraditionalForm
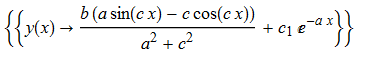
|
|
|
#4
\(y^{\prime }\left ( x\right ) +2xy\left ( x\right ) -xe^{-x^{2}}=0\)
Maple
restart;
ode4:=diff(y(x),x)+2*x*y(x)-x*exp(-x^2)=0:
dsolve(%,y(x));
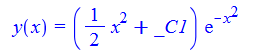
Mathematica
Remove["Global`*"]
ode4=y'[x]+2 x y[x]-x Exp[-x^2]==0;
DSolve[%,y[x],x]// TraditionalForm
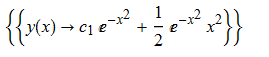
|
|
|
#5
\(y^{\prime }\left ( x\right ) +y\left ( x\right ) \cos \left ( x\right )-e^{2x}=0\)
Maple
restart;
ode5:=diff(y(x),x)+y(x)*cos(x)-exp(2*x)=0:
dsolve(%,y(x));
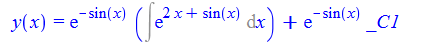
Mathematica
Remove["Global`*"]
ode5=y'[x]+y[x] Cos[x]-Exp[2*x]==0;
DSolve[%,y[x],x]// TraditionalForm
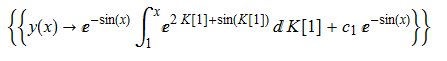
|
|
|
#6
\(y^{\prime }\left ( x\right ) +y\left ( x\right ) \cos \left ( x\right ) -\frac {1}{2}\sin \left ( 2x\right ) =0\)
Maple
restart;
ode6:=diff(y(x),x)+y(x)*cos(x)-1/2*sin(2*x)=0:
dsolve(%,y(x));
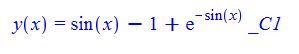
Mathematica
Remove["Global`*"]
ode6=y'[x]+y[x] Cos[x]-1/2 Sin[2 x]==0;
DSolve[%,y[x],x]// TraditionalForm
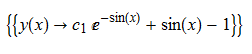
|
|
|
#7
\(y^{\prime }\left ( x\right ) +y\left ( x\right ) \cos \left ( x\right ) -e^{-\sin \left ( x\right ) }=0\)
Maple
restart;
ode7:=diff(y(x),x)+y(x)*cos(x)-exp(-sin(x))=0:
dsolve(%,y(x));
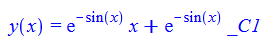
Mathematica
Remove["Global`*"]
ode7=y'[x]+y[x] Cos[x]-Exp[-Sin[x]]==0;
DSolve[%,y[x],x]// TraditionalForm
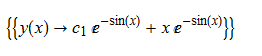
|
|
|
#8
\(y^{\prime }\left ( x\right ) +y\left ( x\right ) \tan \left ( x\right ) -\sin \left ( 2x\right ) =0\)
Maple
restart;
ode8:=diff(y(x),x)+y(x)*tan(x)-sin(2*x)=0:
dsolve(%,y(x));
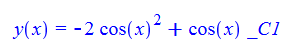
Mathematica
Remove["Global`*"]
ode8=y'[x]+y[x] Tan[x]-Sin[2 x]==0;
DSolve[%,y[x],x]// TraditionalForm
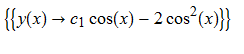
|
|
|
#9
\(y^{\prime }\left ( x\right ) -\left ( \sin \left ( \ln \left ( x\right ) \right ) +\cos \left ( \ln \left ( x\right ) \right ) +a\right ) y\left ( x\right ) =0\)
Maple
restart;
ode9:=diff(y(x),x)-(sin(log(x))+cos(log(x))+a)*y(x)=0:
dsolve(%,y(x));
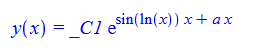
Mathematica
Remove["Global`*"]
ode9=y'[x]-(Sin[Log[x]]+Cos[Log[x]]+a) y[x]==0;
DSolve[%,y[x],x]// TraditionalForm
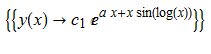
|
|
|
#10
\(y^{\prime }\left ( x\right ) +f^{\prime }\left ( x\right ) y\left ( x\right ) -f\left ( x\right ) f^{\prime }\left ( x\right ) =0\)
Maple
restart;
ode10:=diff(y(x),x)+diff(f(x),x)*y(x)=f(x)*diff(f(x),x);
dsolve(%,y(x));
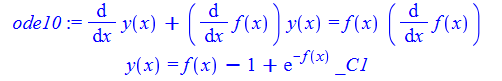
Mathematica
Remove["Global`*"]
ode10=y'[x]+f'[x]*y[x]-f[x]*f'[x]==0;
DSolve[%,y[x],x]// TraditionalForm
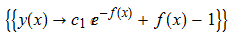
|
|
|
#11
\(y^{\prime }\left ( x\right ) +f\left ( x\right ) y\left ( x\right ) =g\left ( x\right ) \)
Maple
restart;
ode11:=diff(y(x),x)+f(x)*y(x)=g(x);
dsolve(%,y(x));
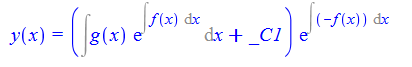
Mathematica
Remove["Global`*"]
ode11=y'[x]+f[x] y[x]==g[x];
First[DSolve[%,y[x],x]]// TraditionalForm
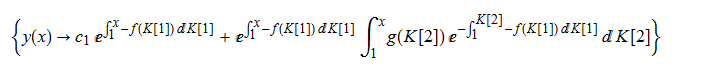
|
|
|
#12
\(y^{\prime }\left ( x\right ) +y\left ( x\right ) ^{2}=1\)
Maple
restart;
ode12:=diff(y(x),x)+(y(x))^2=1:
dsolve(%,y(x));
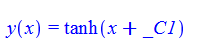
Mathematica
Remove["Global`*"]
ode12=y'[x]+y[x]^2==1;
DSolve[%,y[x],x]// TraditionalForm
ExpToTrig[%]//FullSimplify// TraditionalForm
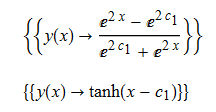
|
|
|
#13
\(y^{\prime }\left ( x\right ) +y\left ( x\right ) ^{2}=ax+b\)
Maple
restart;
ode13:=diff(y(x),x)+(y(x))^2=a*x+b:
dsolve(%,y(x));
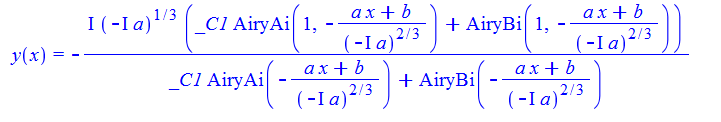
Mathematica
Remove["Global`*"]
ode13=y'[x]+y[x]^2==a x+b;
DSolve[%,y[x],x]// TraditionalForm
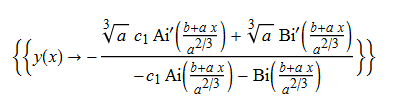
|
|
|
#14
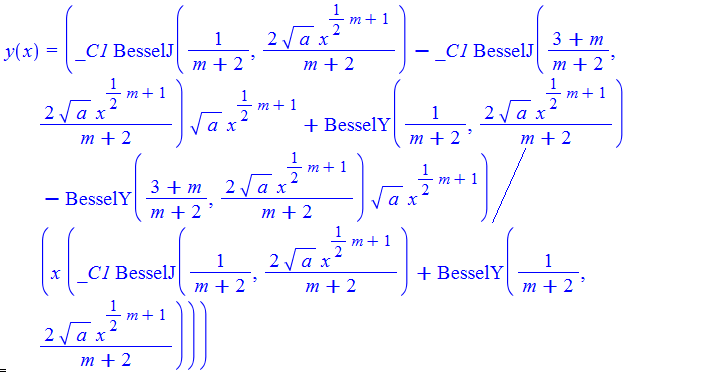
\(y^{\prime }\left ( x\right ) +y\left ( x\right ) ^{2}+ax^{m}=0\)
Maple
restart;
ode14:=diff(y(x),x)+(y(x))^2+a*x^m=0:
dsolve(%,y(x));
Mathematica
Remove["Global`*"]
ode14=y'[x]+y[x]^2+a x^m==0;
DSolve[%,y[x],x]// TraditionalForm
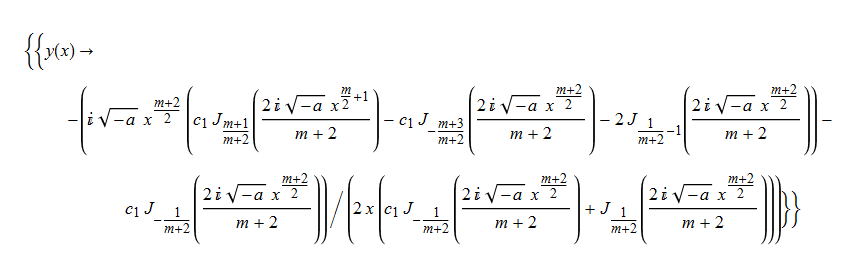
|
|
|
#15
\(y^{\prime }\left ( x\right ) +y\left ( x\right ) ^{2}-2x^{2}y\left ( x\right ) +x^{4}-2x-1=0\)
Maple
restart;
ode15:=diff(y(x),x)+(y(x))^2-2*x^2*y(x)+x^4-2*x-1=0:
dsolve(%,y(x));
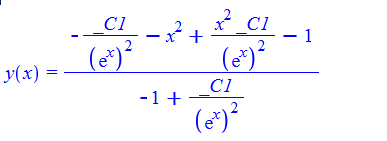
Mathematica
Remove["Global`*"]
ode15 = y'[x] + y[x]^2 - 2 x^2 y[x] + x^4 - 2 x - 1 == 0;
DSolve[%, y[x], x]// TraditionalForm
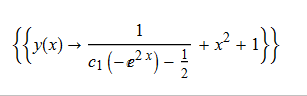
|
|
|
#16
\(y^{\prime }\left ( x\right ) +y\left ( x\right ) ^{2}-\left ( xy\left ( x\right ) -1\right ) f\left ( x\right ) =0\)
Maple
restart;
ode16:=diff(y(x),x)+y(x)^2- (x*y(x)-1)*f(x)=0:
dsolve(%,y(x));
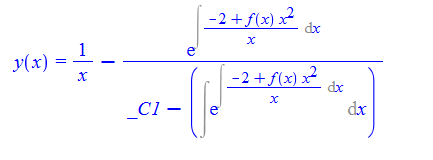
Mathematica
Remove["Global`*"]
ode16 = y'[x] + y[x]^2 + (x*y[x] - 1)*f[x] == 0;
DSolve[%, y[x], x]
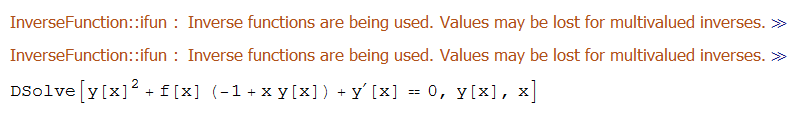
|
|
|
#17
\(y^{\prime }\left ( x\right ) -y\left ( x\right ) ^{2}-3y\left ( x\right ) +4=0\)
Maple
restart;
ode16:=diff(y(x),x)-y(x)^2- 3*y(x)+4=0:
dsolve(%,y(x));
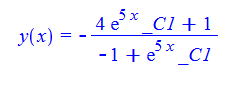
Mathematica
Remove["Global`*"]
ode17 = y'[x] - y[x]^2 - 3*y[x] + 4 == 0;
DSolve[%, y[x], x]// TraditionalForm
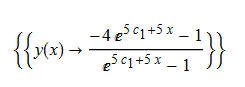
|
|
|
#18
\(y^{\prime }\left ( x\right ) -y\left ( x\right ) ^{2}-xy\left ( x\right ) -x+1=0\)
Maple
restart;
ode18:=diff(y(x),x)-y(x)^2- x*y(x)-x+1=0:
dsolve(%,y(x));
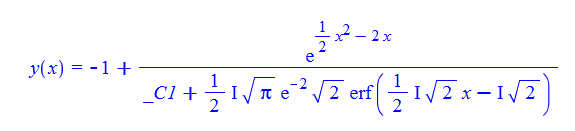
Mathematica
Remove["Global`*"]
ode18 = y'[x] - y[x]^2 - x*y[x] - x + 1 == 0;
DSolve[%, y[x], x]// TraditionalForm
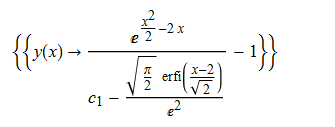
|
|
|
#19
\(y^{\prime }\left ( x\right ) -\left ( y\left ( x\right ) +x\right ) ^{2}=0\)
Maple
restart;
ode19:=diff(y(x),x)-(y(x)+x)^2=0:
dsolve(%,y(x));
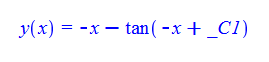
Mathematica
Remove["Global`*"]
ode19=y'[x]-(y[x]+x)^2==0;
DSolve[%,y[x],x]// TraditionalForm
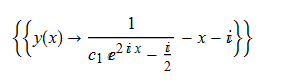
|
|
|
#20
\(y^{\prime }\left ( x\right ) -y\left ( x\right ) ^{2}+\left ( x^{2}+1\right ) y\left ( x\right ) -2x=0\)
Maple
restart;
ode20:=diff(y(x),x)-y(x)^2+(x^2+1)*y(x)-2*x=0:
dsolve(%,y(x));
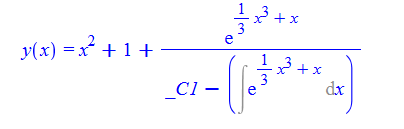
Mathematica
Remove["Global`*"]
ode20=y'[x]-y[x]^2+(x^2+1)*y[x]-2*x==0;
DSolve[%,y[x],x]// TraditionalForm
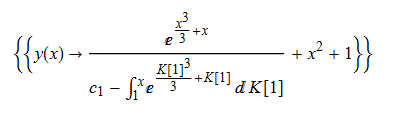
|
|
|
#21
\(y^{\prime }\left ( x\right ) -y\left ( x\right ) ^{2}+y\left ( x\right ) \sin \left ( x\right ) -\cos \left ( x\right ) =0\)
Maple
restart;
ode21:=diff(y(x),x)-y(x)^2+y(x)*sin(x)-cos(x)=0:
dsolve(%,y(x));
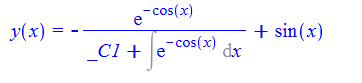
Mathematica
Remove["Global`*"]
ode21=y'[x]-y[x]^2+y[x]*Sin[x]-Cos[x]==0;
DSolve[%,y[x],x]// TraditionalForm
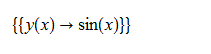
|
|
|
#22
\(y^{\prime }\left ( x\right ) -y\left ( x\right ) ^{2}-y\left ( x\right ) \sin \left ( 2x\right ) -\cos \left ( 2x\right ) =0\)
Maple
restart;
ode22:=diff(y(x),x)-sin(2*x)*y(x)-y(x)^2=0;
dsolve(%,y(x));
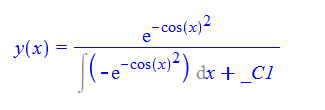
Mathematica
Remove["Global`*"]
ode22=y'[x]-y[x]^2-y[x]*Sin[2*x]-Cos[2*x]==0
DSolve[%,y[x],x]
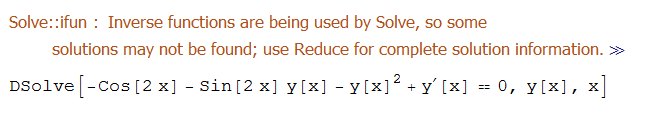
|
|
|
#23
\(y^{\prime }\left ( x\right ) +ay\left ( x\right ) ^{2}-b=0\)
Maple
restart;
ode23:=diff(y(x),x)+a*y(x)^2-b=0:
dsolve(%,y(x));
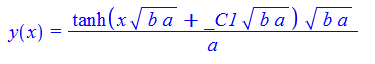
Mathematica
Remove["Global`*"]
ode23=y'[x]+a*y[x]^2-b==0;
DSolve[%,y[x],x]// TraditionalForm
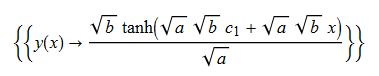
|
|
|
#24
\(y^{\prime }\left ( x\right ) +ay\left ( x\right ) ^{2}-bx^{\nu }=0\)
Maple
restart;
ode24:=diff(y(x),x)+a*y(x)^2-b*x^nu=0:
dsolve(%,y(x));
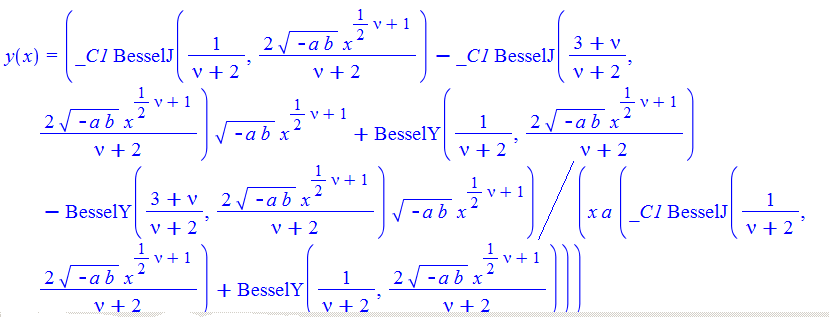
Mathematica
Remove["Global`*"]
ode24=y'[x]+a*y[x]^2-b*x^nu==0;
DSolve[%,y[x],x]//TraditionalForm
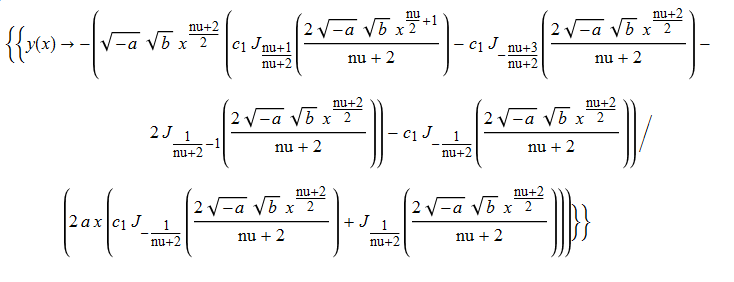
|
|
|
#25
\(y^{\prime }\left ( x\right ) +ay\left ( x\right ) ^{2}-bx^{2\nu }-cx^{\nu -1}=0\)
Maple
restart;
ode25:=diff(y(x),x)+a*y(x)^2-b*x^(2*nu)-c*x^(nu-1)=0:
dsolve(%,y(x));
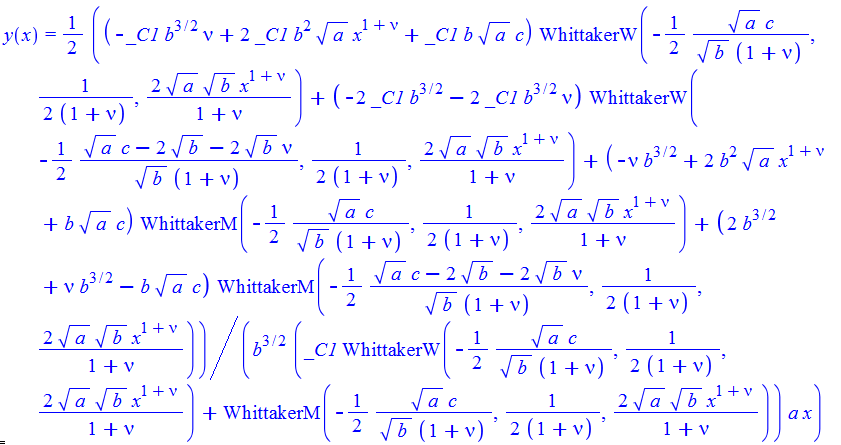
Mathematica
Remove["Global`*"]
ode25=y'[x]+a*y[x]^2-b*x^(2*\[Nu])-c*x^(\[Nu]-1)==0
DSolve[%,y[x],x]// Simplify // TraditionalForm
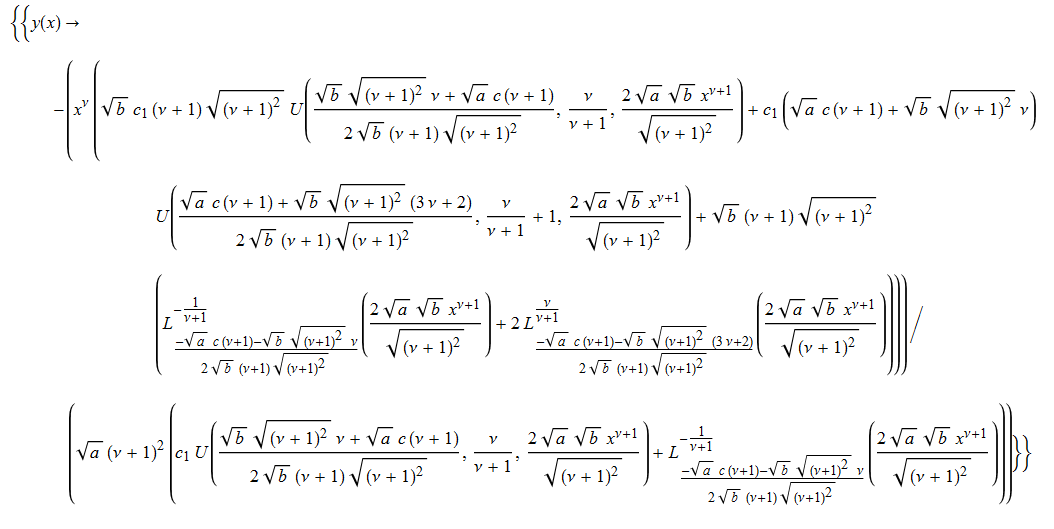
|
|
|
#26
\(y^{\prime }\left ( x\right ) -\left ( Ay\left ( x\right ) -a\right ) \left ( By\left ( x\right ) -b\right ) =0\)
Maple
restart;
ode26:=diff(y(x),x)-(A*y(x)-a)*(B*y(x)-b)=0:
dsolve(%,y(x));
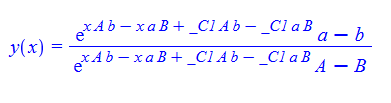
Mathematica
Remove["Global`*"]
ode26=y'[x]-(A*y[x]-a)*(B*y[x]-b)==0;
DSolve[%,y[x],x]//TraditionalForm
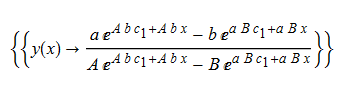
|
|
|
#27
\(y^{\prime }\left ( x\right ) +ay\left ( x\right ) \left ( y\left ( x\right ) -x\right ) -1=0\)
Maple
restart;
ode27:=diff(y(x),x)+a*y(x)*(y(x)-x)-1=0:
dsolve(%,y(x));
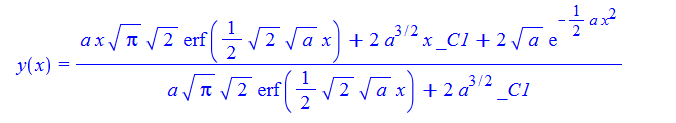
Mathematica
Remove["Global`*"]
ode27=y'[x]+a*y[x]*(y[x]-x)-1==0;
DSolve[%,y[x],x]//TraditionalForm
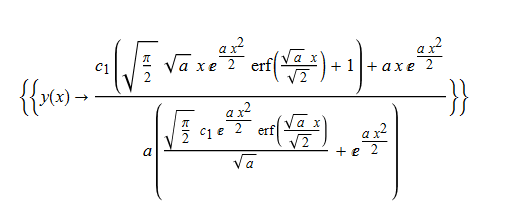
|
|
|
#28
\(y^{\prime }\left ( x\right ) +xy\left ( x\right ) ^{2}-x^{3}y\left ( x\right ) -2x=0\)
Maple
restart;
ode28:=diff(y(x),x)+x*y(x)^2-x^3*y(x)-2*x=0;
dsolve(%,y(x));
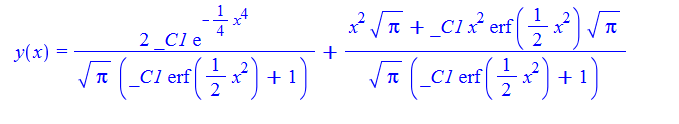
Mathematica
Remove["Global`*"]
ode28=y'[x]+x*y[x]^2-x^3*y[x]-2*x==0;
DSolve[%,y[x],x]//TraditionalForm
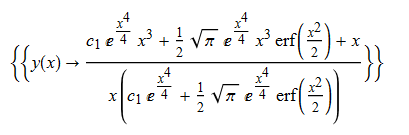
|
|
|
#29
\(y^{\prime }\left ( x\right ) -xy\left ( x\right ) ^{2}-3xy\left ( x\right )=0\)
Maple
restart;
ode29:=diff(y(x),x)-x*y(x)^2-3*x*y(x)=0:
dsolve(%,y(x));
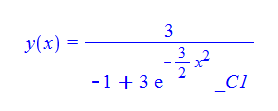
Mathematica
Remove["Global`*"]
ode29=y'[x]-x*y[x]^2-3*x*y[x]==0;
DSolve[%,y[x],x]//TraditionalForm
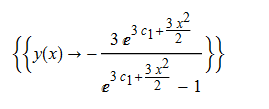
|
|
|
#30
\(y^{\prime }\left ( x\right ) +x^{\left ( -1-a\right ) }y\left ( x\right ) ^{2}-x^{a}=0\)
Maple
restart;
ode30:=diff(y(x),x)+x^(-1-a)*y(x)^2-x^a=0:
dsolve(%,y(x));

Mathematica
Remove["Global`*"]
ode30=y'[x]+x^(-a-1)*y[x]^2-x^a==0
DSolve[%,y[x],x]

|
|
|
#31
\(y^{\prime }\left ( x\right ) -ax^{n}\left ( y\left ( x\right ) ^{2}+1\right ) =0\)
Maple
restart;
ode31:=diff(y(x),x)-a*x^n*(y(x)^2+1)=0:
dsolve(%,y(x));
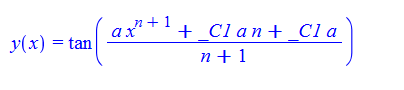
Mathematica
Remove["Global`*"]
ode31 = y'[x] - a*x^n*(y[x]^2 + 1) == 0;
DSolve[%, y[x], x] // TraditionalForm
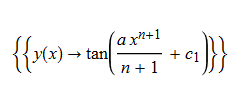
|
|
|
#32
\(y^{\prime }\left ( x\right ) +y\left ( x\right ) ^{2}\sin \left ( x\right ) -2\frac {\sin \left ( x\right ) }{\cos \left ( x\right ) ^{2}}=0\)
Maple
restart;
ode31:=diff(y(x),x)+y(x)^2*sin(x)-2*sin(x)/cos(x)^2=0:
dsolve(%,y(x));
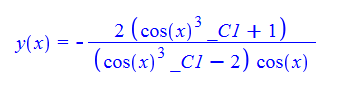
Mathematica
Remove["Global`*"]
ode32=y'[x]+y[x]^2*Sin[x]-2*Sin[x]/Cos[x]^2==0;
DSolve[%,y[x],x]//TraditionalForm
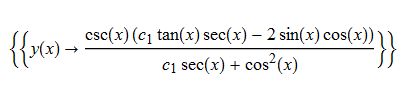
|
|
|
#33
\(y^{\prime }\left ( x\right ) -\frac {y(x)^{2}f^{\prime }\left ( x\right ) }{g\left ( x\right ) }+\frac {g^{\prime }\left ( x\right ) }{f\left ( x\right ) }=0\)
Maple
restart;
ode33:=diff(y(x),x)-y(x)^2*diff(f(x),x)/g(x)+diff(g(x),x)/f(x)=0;
dsolve(%,y(x));
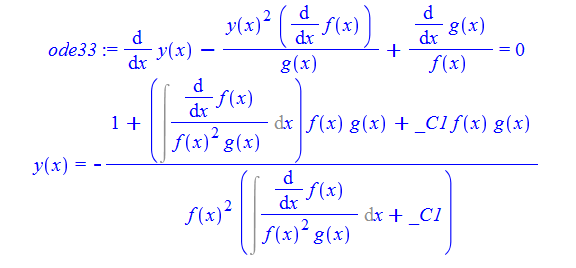
Mathematica
Remove["Global`*"]
(ode33=y'[x]-y[x]^2*D[f[x],x]/g[x]+D[g[x],x]/f[x]==0)//TraditionalForm
DSolve[ode33,y[x],x]//TraditionalForm
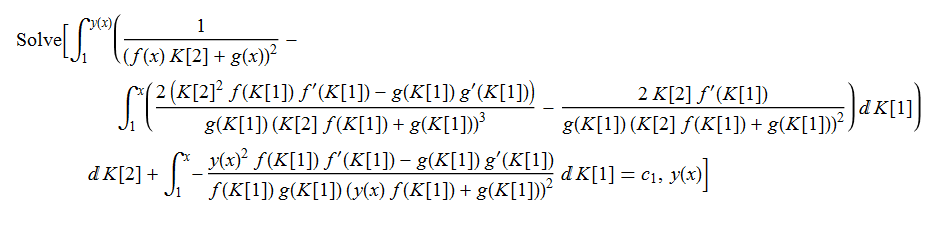
|
|
|
#34
\(y^{\prime }\left ( x\right ) +f\left ( x\right ) y\left ( x\right ) ^{2}+g\left ( x\right ) y\left ( x\right ) =0\)
Maple
restart;
ode34:=diff(y(x),x)+f(x)*y(x)^2+g(x)*y(x)=0:
dsolve(%,y(x));
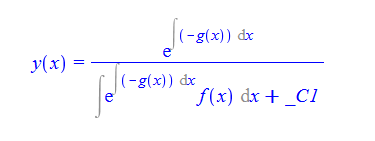
Mathematica
Remove["Global`*"]
ode34=y'[x]+f[x]*y[x]^2+g[x]*y[x]==0
DSolve[%,y[x],x]//TraditionalForm
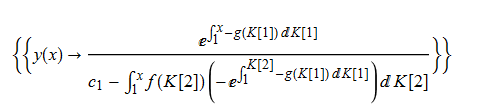
|
|
|
#35
\(y^{\prime }\left ( x\right ) +f\left ( x\right ) \left ( y\left ( x\right ) ^{2}+2ay\left ( x\right ) +b\right ) =0\)
Maple
restart;
ode35:=diff(y(x),x)+f(x)*(y(x)^2+2*a*y(x)+b)=0:
dsolve(%,y(x));
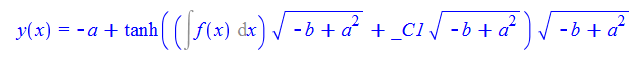
Mathematica
Remove["Global`*"]
ode35 = y'[x] + f[x]*(y[x]^2 + 2*a*y[x] + b) == 0;
DSolve[%, y[x], x] // TraditionalForm
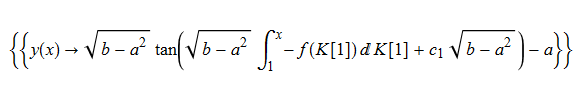
|
|
|
#36
\(y^{\prime }\left ( x\right ) +y\left ( x\right ) ^{3}+axy\left ( x\right ) ^{2}=0\)
Maple
restart;
ode36:=diff(y(x),x)+y(x)^3+a*x*y(x)^2=0:
dsolve(%,y(x));
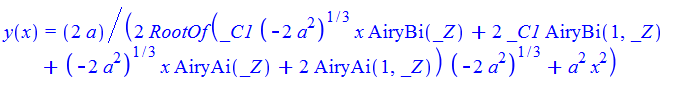
Mathematica
Remove["Global`*"]
ode36 = y'[x] + y[x]^3 + a*x*y[x]^2 == 0
DSolve[%, y[x], x] // TraditionalForm
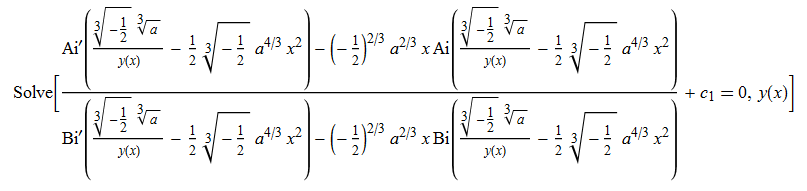
|
|
|
#37
\(y^{\prime }\left ( x\right ) -y\left ( x\right ) ^{3}-ae^{x}y\left ( x\right ) ^{2}=0\)
Maple
restart;
ode37:=diff(y(x),x)-y(x)^3-a*exp(x)*y(x)^2=0:
dsolve(%,y(x));
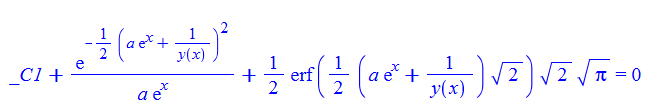
Mathematica
Remove["Global`*"]
ode37 = y'[x] - y[x]^3 - a*Exp[x]*y[x]^2 == 0
DSolve[%, y[x], x] // TraditionalForm
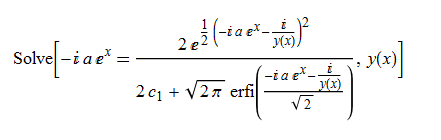
|
|
|
#38
\(y^{\prime }\left ( x\right ) -ay\left ( x\right ) ^{3}-bx^{\frac {3}{2}}=0\)
Maple
restart;
ode38:=diff(y(x),x)-a*y(x)^3-b*x^(3/2)=0:
dsolve(%,y(x));
Nothing returned
Mathematica
Remove["Global`*"]
ode38 = y'[x] - a*y[x]^3 - b*x^(3/2) == 0
DSolve[%, y[x], x] // TraditionalForm
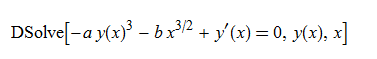
|
|
|
#39
\(y^{\prime }\left ( x\right ) -a_{3}y\left ( x\right ) ^{3}-a_{2}y\left ( x\right ) ^{2}-a_{1}y\left ( x\right ) -a_{0}=0\)
Maple
restart;
ode39:=diff(y(x),x)-a3*y(x)^3-a2*y(x)^2-a1*y(x)-a0=0:
dsolve(%,y(x));
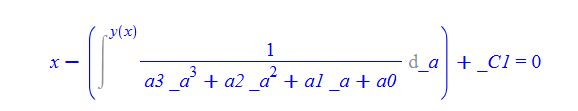
Mathematica
Remove["Global`*"]
ode39 = y'[x] - a3*y[x]^3 - a2*y[x]^2 - a1*y[x] - a0 == 0
DSolve[%, y[x], x] // TraditionalForm
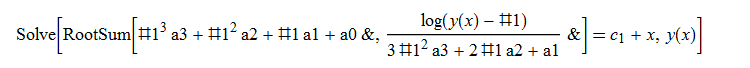
|
|
|
#40
\(y^{\prime }\left ( x\right ) +3ay\left ( x\right ) ^{3}+6axy\left ( x\right ) ^{2}=0\)
Maple
restart;
ode40:=diff(y(x),x)+3*a*y(x)^3+6*a*x*y(x)^2=0:
dsolve(%,y(x));
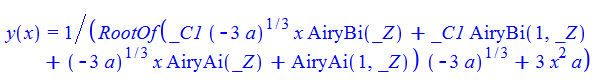
Mathematica
Remove["Global`*"]
ode40 = y'[x] + 3*a*y[x]^3 + 6*a*x*y[x]^2 == 0
DSolve[%, y[x], x] // TraditionalForm
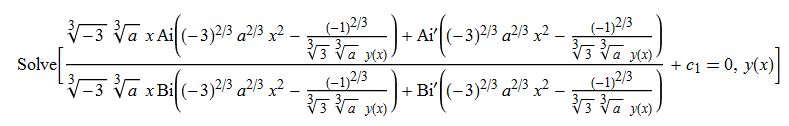
|
|
|
#41
\(y^{\prime }\left ( x\right ) +axy\left ( x\right ) ^{3}+by\left ( x\right ) ^{2}=0\)
Maple
restart;
ode41:=diff(y(x),x)+a*x*y(x)^3+b*y(x)^2=0:
dsolve(%,y(x));
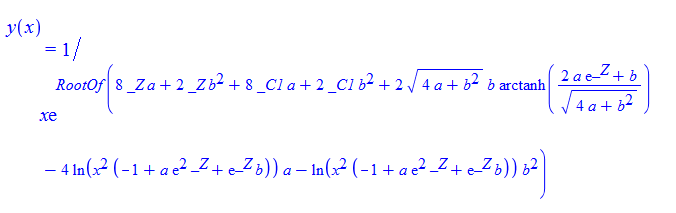
Mathematica
Remove["Global`*"]
ode41 = y'[x] + a*x*y[x]^3 + b*y[x]^2 == 0
DSolve[%, y[x], x] // TraditionalForm
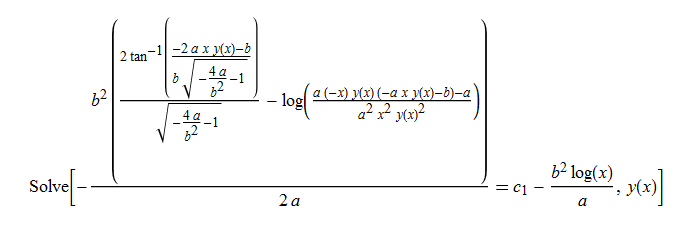
|
|
|
#42
\(y^{\prime }\left ( x\right ) -x\left ( x+2\right ) y\left ( x\right ) ^{3}-\left ( x+3\right ) y\left ( x\right ) ^{2}=0\)
Maple
restart;
ode42:=diff(y(x),x)-x*(x+2)*y(x)^3-(x+3)*y(x)^2=0:
dsolve(%,y(x));
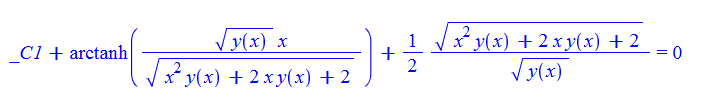
Mathematica
Remove["Global`*"]
ode42 = y'[x] - x*(x + 2)*y[x]^3 - (x + 3)*y[x]^2 == 0
DSolve[%, y[x], x] // TraditionalForm
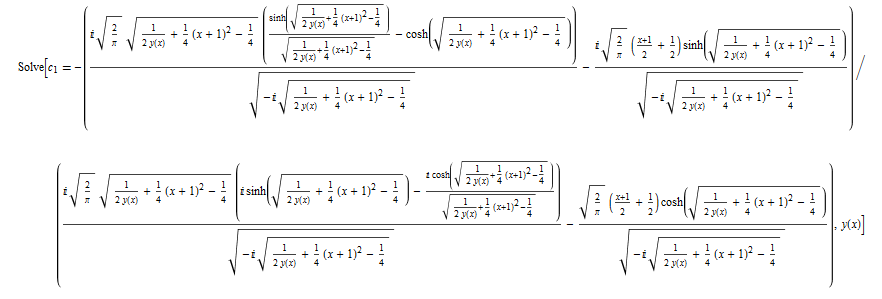
|
|
|
#43
\(y^{\prime }\left ( x\right ) +\left ( 3ax^{2}+4a^{2}x+b\right ) y\left ( x\right ) ^{3}+3xy\left ( x\right ) ^{2}=0\)
Maple
restart;
ode43:=diff(y(x),x)+(3*a*x^2+4*a^2*x+b)*y(x)^3+3*x*y(x)^2=0:
dsolve(%,y(x));

Mathematica
Remove["Global`*"]
ode43 = y'[x] + (3*a*x^2 + 4*a^2*x + b)*y[x]^3 + 3*x*y[x]^2 == 0
DSolve[%, y[x], x] // TraditionalForm
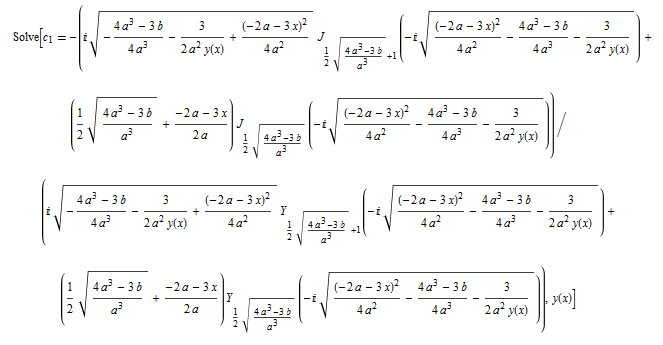
|
|
|
#44
\(y^{\prime }\left ( x\right ) +2ax^{3}y\left ( x\right ) ^{3}+2xy\left ( x\right ) =0\)
Maple
restart;
ode44:=diff(y(x),x)+2*a*x^3*y(x)^3+2*x*y(x)=0:
dsolve(%,y(x));
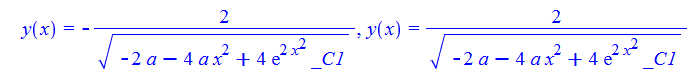
Mathematica
Remove["Global`*"]
ode44 = y'[x] + 2*a*x^3*y[x]^3 + 2*x*y[x] == 0
DSolve[%, y[x], x] // TraditionalForm
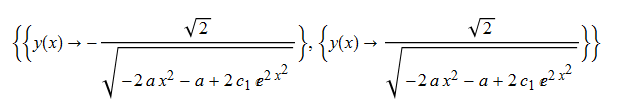
|
|
|
#45
\(y^{\prime }\left ( x\right ) +2\left ( a^{2}x^{3}-b^{2}x\right ) y\left ( x\right ) ^{3}+3by\left ( x\right ) ^{2}=0\)
Maple
restart;
ode45:=diff(y(x),x)+2*(a^2*x^3-b^2*x)*y(x)^3+3*b*y(x)^2=0:
dsolve(%,y(x));
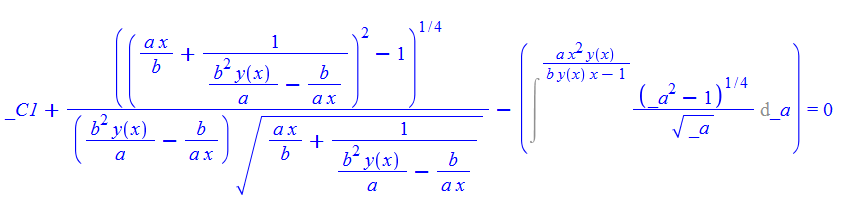
Mathematica
Remove["Global`*"]
ode45 = y'[x] + 2*(a^2*x^3 - b^2*x)*y[x]^3 + 3*b*y[x]^2 == 0
DSolve[%, y[x], x] // TraditionalForm
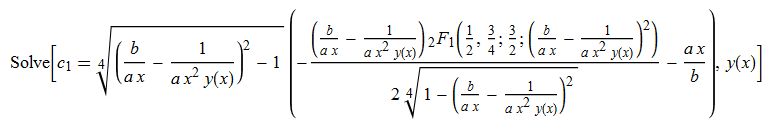
|
|
|
#46
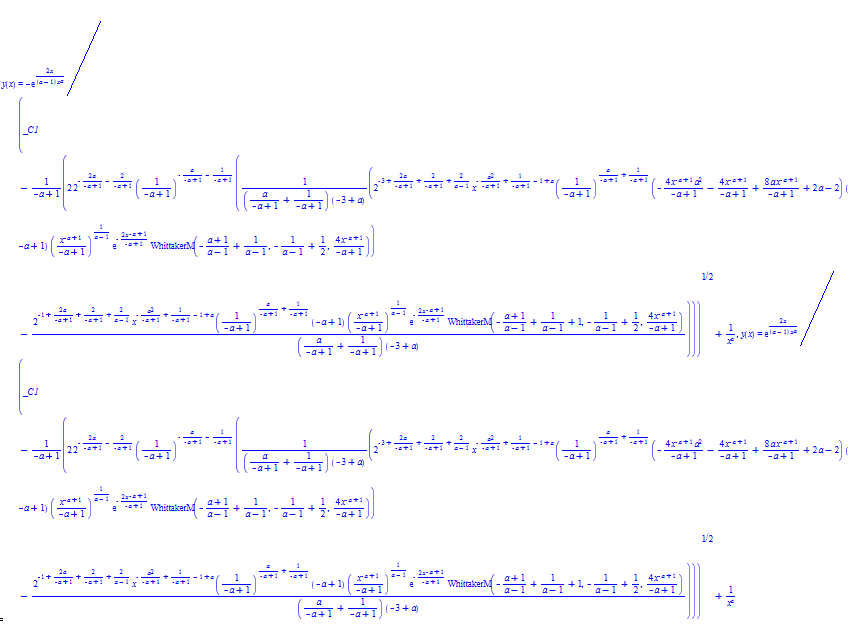
\(y^{\prime }\left ( x\right ) -x^{a}y\left ( x\right ) ^{3}+3y\left ( x\right ) ^{2}-x^{-a}y\left ( x\right ) -x^{-2a}+ax^{-a-1}=0\)
Maple
restart;
ode46:=diff(y(x),x)-x^a*y(x)^3+3*y(x)^2-x^(-a)*y(x)-x^(-2*a)+a*x^(-a-1)=0:
dsolve(%,y(x));
 Mathematica Mathematica
Remove["Global`*"]
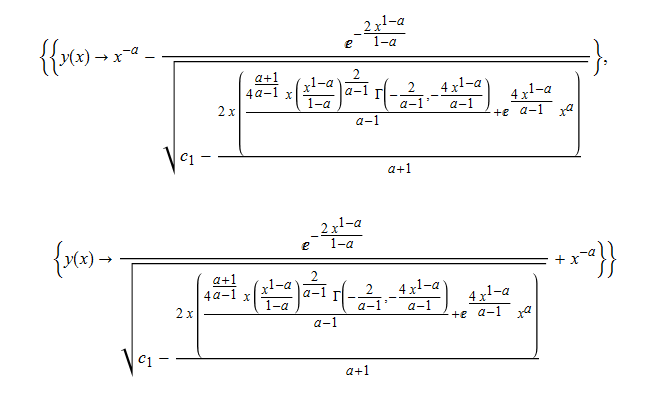
ode46=y'[x]-x^a*y[x]^3+3*y[x]^2-x^(-a)*y[x]-x^(-2*a)+a*x^(-a-1)==0
DSolve[%, y[x], x] // TraditionalForm
|
|
|
#47
\(y^{\prime }\left ( x\right ) -a\left ( x^{n}-x\right ) y\left ( x\right ) ^{3}-y\left ( x\right ) ^{2}=0\)
Maple
restart;
ode47:=diff(y(x),x)-a*(x^n-x)*y(x)^3-y(x)^2=0:
dsolve(%,y(x));
No output
Mathematica
Remove["Global`*"]
ode47 = y'[x] - a*(x^n - x)*y[x]^3 - y[x]^2 == 0
DSolve[%, y[x], x] // TraditionalForm
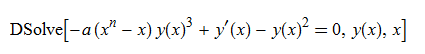
|
|
|
#48
\(y^{\prime }\left ( x\right ) -\left ( ax^{n}+bx\right ) y\left ( x\right ) ^{3}-cy\left ( x\right ) ^{2}=0\)
Maple
restart;
ode48:=diff(y(x),x)-(a*x^n+b*x)*y(x)^3-c*y(x)^2=0:
dsolve(%,y(x));
No output
Mathematica
Remove["Global`*"]
ode48 = y'[x] - (a*x^n + b*x)*y[x]^3 - c*y[x]^2 == 0
DSolve[%, y[x], x] // TraditionalForm
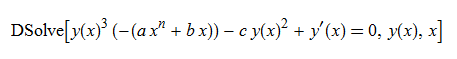
|
|
|
#49
\(y^{\prime }\left ( x\right ) +a\phi ^{\prime }\left ( x\right ) y\left ( x\right ) ^{3}+6a\phi \left ( x\right ) y\left ( x\right ) ^{2}+\left ( 2a+1\right ) y\left ( x\right ) \frac {\phi ^{\prime \prime }\left ( x\right ) }{\phi ^{\prime }\left ( x\right ) }+2a+2=0\)
Maple
restart;
ode49:=diff(y(x),x)+a*diff(phi(x),x)*y(x)^3+6*a*phi(x)*y(x)^2+(2*a+1)*y(x)*diff(phi(x),x$2)/diff(phi(x),x)+2*a+2=0;
dsolve(%,y(x));
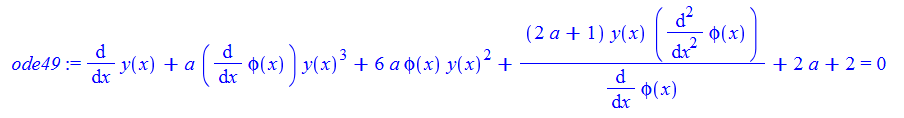
Mathematica
Remove["Global`*"]
ode49 = y'[x] + a*phi'[x]*y[x]^3 +
6*a*phi[x]*y[x]^2 + (2*a + 1)*y[x]*phi''[x]/phi'[x] + 2*a + 2 == 0
DSolve[%, y[x], x] // TraditionalForm
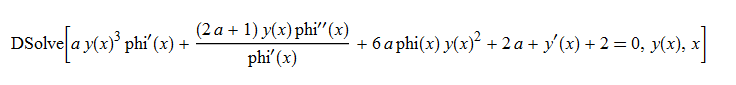
|
|
|
#50
\(y^{\prime }\left ( x\right ) -f_{3}\left ( x\right ) y\left ( x\right ) ^{3}-f_{2}\left ( x\right ) y\left ( x\right ) ^{2}-f_{1}\left ( x\right ) y\left ( x\right ) -f_{0}\left ( x\right ) =0\)
Maple
restart;
ode50:=diff(y(x),x)-f3(x)*y(x)^3-f2(x)*y(x)^2-f1(x)*y(x)-f0(x)=0;
dsolve(%,y(x));
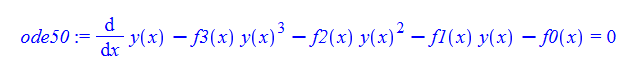
Mathematica
Remove["Global`*"]
ode50 = y'[x] - f3[x]*y[x]^3 - f2[x]*y[x]^2 - f1[x]*y[x] - f0[x] == 0
DSolve[%, y[x], x] // TraditionalForm
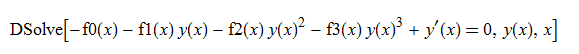
|
|
|
#51
\(y^{\prime }\left ( x\right ) -\left ( y\left ( x\right ) -f\left ( x\right ) \right ) \left ( y\left ( x\right ) -g\left ( x\right ) \right ) \left ( y\left ( x\right ) -\frac {af\left ( x\right ) +bg\left ( x\right ) }{a+b}\right ) h\left ( x\right ) -\frac {f^{\prime }\left ( x\right ) \left ( y\left ( x\right ) -g\left ( x\right ) \right ) }{f\left ( x\right ) -g\left ( x\right ) }-\frac {g^{\prime }\left ( x\right ) \left ( y\left ( x\right ) -f\left ( x\right ) \right ) }{g\left ( x\right ) -f\left ( x\right ) }=0\)
Maple
restart;
ode51:=diff(y(x),x)-(y(x)-f(x))*(y(x)-g(x))*(y(x)-(a*f(x)+b*g(x))/(a+b))*h(x)-
diff(f(x),x)*(y(x)-g(x))/(f(x)-g(x))-diff(g(x),x)*(y(x)-f(x))/(g(x)-f(x))=0;
dsolve(%,y(x));

Mathematica
Remove["Global`*"]
ode51 = D[y[x],x] - (y[x] - f[x])*(y[x] -g[x])*(y[x] - (a*f[x] + b*g[x])/(a + b))*h[x] -
D[f[x], x]*(y[x] - g[x])/(f[x] - g[x])-D[g[x], x]*(y[x] - f[x])/(g[x] - f[x]) == 0
DSolve[%, y[x], x] // TraditionalForm
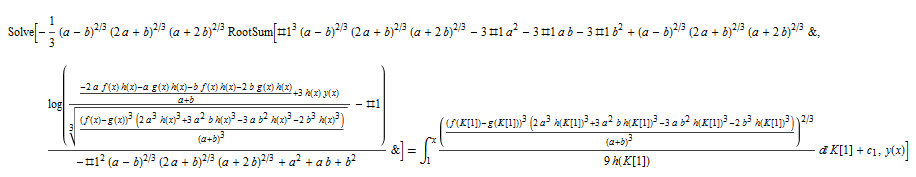
|
|
|
#52
\(y^{\prime }\left ( x\right ) -bx^{\frac {n}{1-n}}-ay\left ( x\right ) ^{n}=0\)
Maple
restart;
ode52:=diff(y(x),x)-b*x^(n/(1-n))-a*y(x)^n=0;
dsolve(%,y(x));
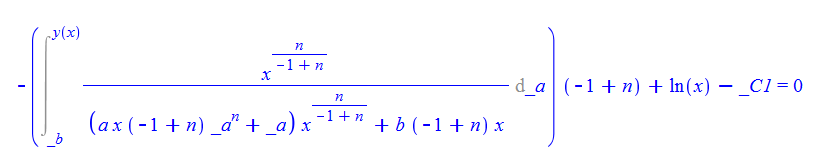
Mathematica
Remove["Global`*"]
ode52 = D[y[x], x] - a*y[x]^n - b*x^(n/(1 - n)) == 0
DSolve[%, y[x], x] // TraditionalForm
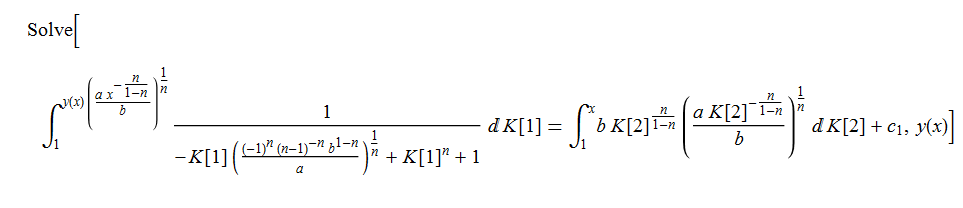
|
|
|
#53
\(y^{\prime }\left ( x\right ) -\frac {y\left ( x\right ) f^{\prime }\left ( x\right ) }{f\left ( x\right ) }-f\left ( x\right ) g^{\prime }\left ( x\right ) -f\left ( x\right ) ^{1-n}\left ( b+ag\left ( x\right ) \right ) ^{-n}y\left ( x\right ) ^{n}g^{\prime }\left ( x\right ) =0\)
Maple
restart;
ode53:=diff(y(x),x)-(y(x)*diff(f(x),x))/f(x)-f(x)*diff(g(x),x)-
f(x)^(1-n)/(b+a*g(x))^n*y(x)^n*diff(g(x),x)=0;
dsolve(%,y(x));
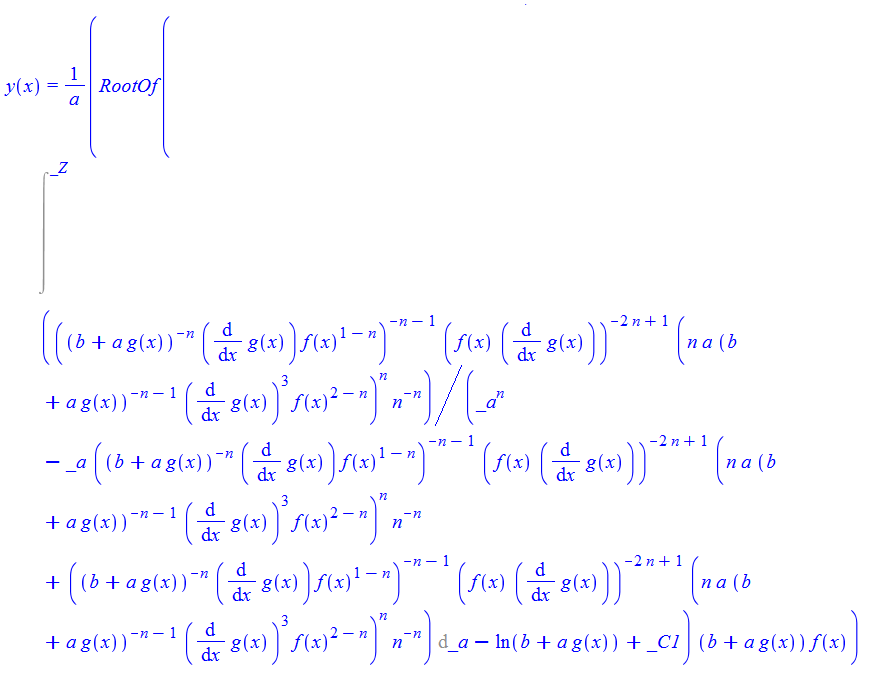
Mathematica
Remove["Global`*"]
ode53 = y'[x] - f[x]^(1 - n)*g'[x]*y[x]^n/(a*g[x] + b)^n -
f'[x]*y[x]/f[x] - f[x]*g'[x] == 0
DSolve[%, y[x], x] // TraditionalForm
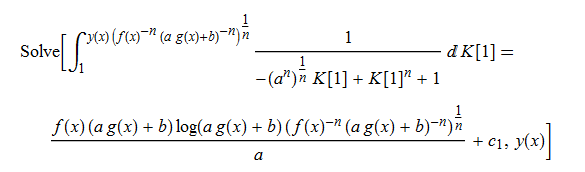
|
|
|
#54
\(y^{\prime }\left ( x\right ) -a^{n}f\left ( x\right ) ^{1-n}y\left ( x\right ) ^{n}g^{\prime }\left ( x\right ) -\frac {y\left ( x\right ) f^{\prime }\left ( x\right ) }{f\left ( x\right ) }-f\left ( x\right ) g^{\prime }\left ( x\right ) =0\)
Maple
restart;
ode54:=diff(y(x),x)-a^n*f(x)^(1-n)*diff(g(x),x)*y(x)^n-(diff(f(x),x)*y(x))/f(x)-f(x)*diff(g(x),x)=0:
dsolve(%,y(x));
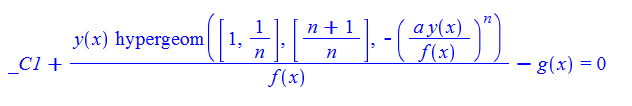
Mathematica
Remove["Global`*"]
ode54=y'[x]-a^n*f[x]^(1-n)*g'[x]*y[x]^n-f'[x]*y[x]/f[x]-f[x]*g'[x]==0
DSolve[%,y[x],x]//TraditionalForm
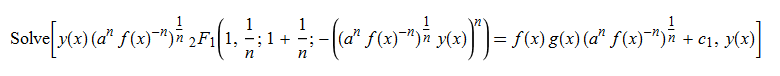
|
|
|
#55
\(y^{\prime }\left ( x\right ) -f\left ( x\right ) y\left ( x\right ) ^{n}-g\left ( x\right ) y\left ( x\right ) -h\left ( x\right ) =0\)
Maple
restart;
ode55:=diff(y(x),x)-f(x)*y(x)^n-g(x)*y(x)-h(x)=0:
dsolve(%,y(x));
No answer |
|
Mathematica
Remove["Global`*"]
ode55 = y'[x] - f[x]*y[x]^n - g[x]*y[x] - h[x] == 0
DSolve[%, y[x], x] // TraditionalForm
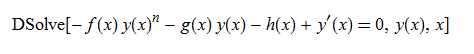
|
|
|
#56
\(y^{\prime }\left ( x\right ) -f\left ( x\right ) y\left ( x\right ) ^{a}-g\left ( x\right ) y\left ( x\right ) ^{b}=0\)
Maple
restart;
ode56:=diff(y(x),x)-f(x)*y(x)^a-g(x)*y(x)^b=0:
dsolve(%,y(x));
No answer
Mathematica
Remove["Global`*"]
ode56=y'[x]-f[x]*y[x]^a-g[x]*y[x]^b==0
DSolve[%,y[x],x]//TraditionalForm
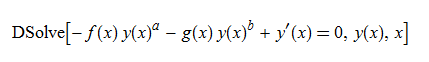
|
|
|
#57
\(y^{\prime }\left ( x\right ) -\sqrt {\left \vert y\left ( x\right ) \right \vert }=0\)
Maple
restart;
ode57:=diff(y(x),x)-sqrt(abs(y(x)))=0:
dsolve(%,y(x));
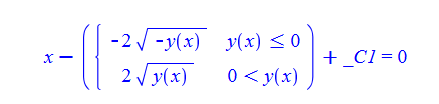
Mathematica
Remove["Global`*"]
ode57=y'[x]-Abs[y[x]]^(1/2)==0
DSolve[%,y[x],x]//TraditionalForm
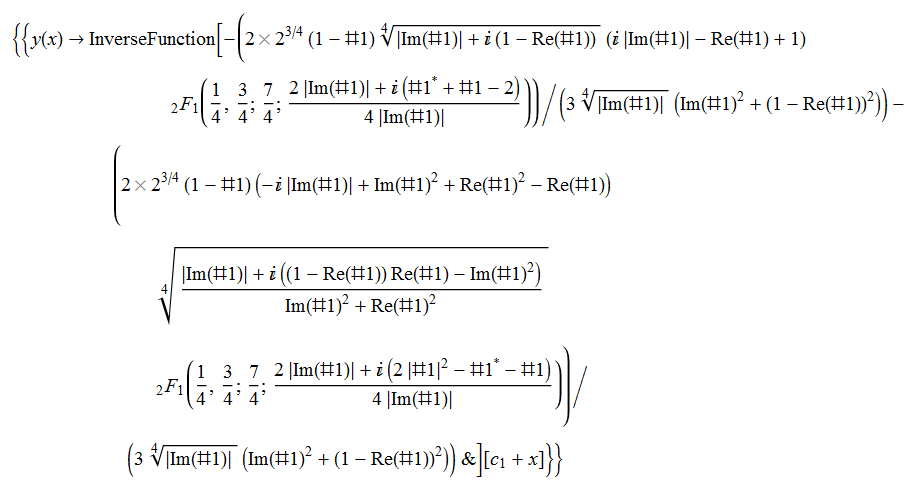
|
|
|
#58
\(y^{\prime }\left ( x\right ) -ay\left ( x\right ) ^{\frac {1}{2}}-bx=0\)
Maple
restart;
ode58:=diff(y(x),x)-a*y(x)^(1/2)-b*x=0:
dsolve(%,y(x));
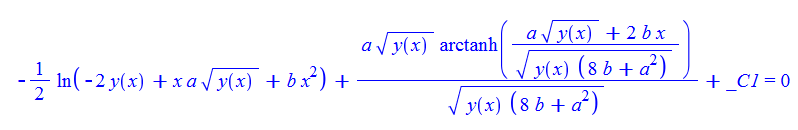
Mathematica
Remove["Global`*"]
ode58 = y'[x] - a*y[x]^(1/2) - b*x == 0
DSolve[%, y[x], x] // TraditionalForm
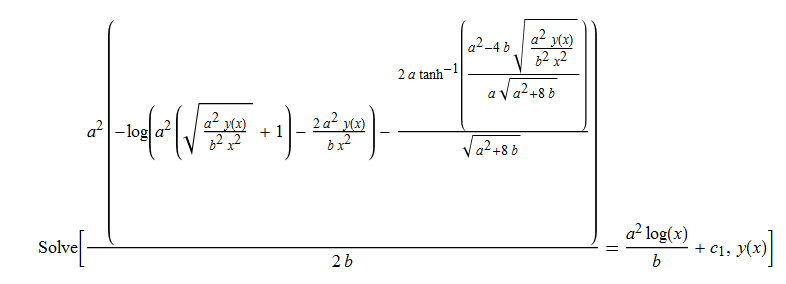
|
|
|
#59
\(y^{\prime }\left ( x\right ) -a\left ( y\left ( x\right ) ^{2}+1\right ) ^{\frac {1}{2}}-b=0\)
Maple
restart;
ode59:=diff(y(x),x)-a*(y(x)^2+1)^(1/2)-b=0:
dsolve(%,y(x));
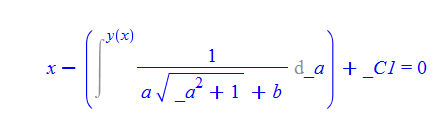
Mathematica
Remove["Global`*"]
ode59 = y'[x] - a*(y[x]^2 + 1)^(1/2) - b == 0
DSolve[%, y[x], x] // TraditionalForm
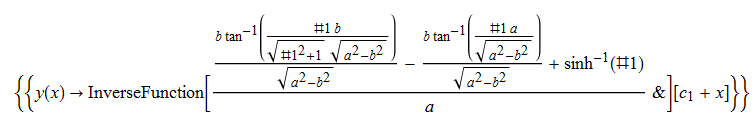
|
|
|
#60
\(y^{\prime }\left ( x\right ) -\frac {\left ( y\left ( x\right ) ^{2}-1\right ) ^{\frac {1}{2}}}{\left ( x^{2}-1\right ) ^{\frac {1}{2}}}=0\)
Maple
restart;
ode60:=diff(y(x),x)-(y(x)^2-1)^(1/2)/(x^2-1)^(1/2)=0:
dsolve(%,y(x));
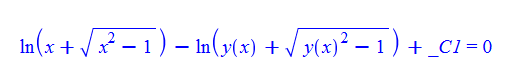
Mathematica
Remove["Global`*"]
ode60 = y'[x] - (y[x]^2 - 1)^(1/2)/(x^2 - 1)^(1/2) == 0
DSolve[%, y[x], x] // TraditionalForm
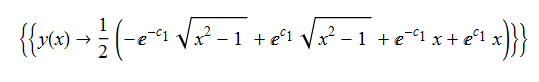
|
|
|
#61
\(y^{\prime }\left ( x\right ) -\frac {\left ( x^{2}-1\right ) ^{\frac {1}{2}}}{\left ( y\left ( x\right ) ^{2}-1\right ) ^{\frac {1}{2}}}=0\)
Maple
restart;
ode61:=diff(y(x),x)-(x^2-1)^(1/2)/(y(x)^2-1)^(1/2)=0:
dsolve(%,y(x));
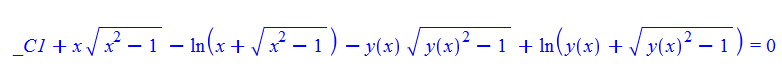
Mathematica
Remove["Global`*"]
ode61 = y'[x] - (x^2 - 1)^(1/2)/(y[x]^2 - 1)^(1/2) == 0
DSolve[%, y[x], x] // TraditionalForm
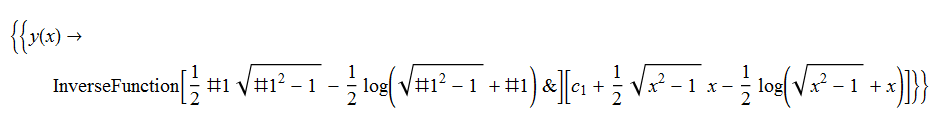
|
|
|
#62
\(y^{\prime }\left ( x\right ) -\frac {y\left ( x\right ) -x^{2}\sqrt {x^{2}-y\left ( x\right ) ^{2}}}{x+xy\left ( x\right ) \sqrt {x^{2}-y\left ( x\right ) ^{2}}}=0\)
Maple
restart;
ode62:=diff(y(x),x)-(y(x)-x^2*(x^2-y(x)^2)^(1/2))/(x+x*y(x)*(x^2-y(x)^2)^(1/2))=0:
dsolve(%,y(x));
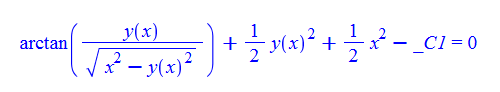
Mathematica
Remove["Global`*"]
ode62 = D[y[x],x] - (y[x] -
x^2*(x^2 - y[x]^2)^(1/2))/(x*y[x]*(x^2 - y[x]^2)^(1/2) + x)==0;
DSolve[%, y[x], x] // TraditionalForm
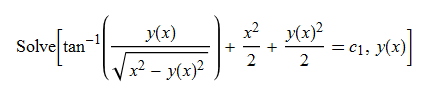
|
|
|
#63
\(y^{\prime }\left ( x\right ) -\frac {1+y\left ( x\right ) ^{2}}{\left ( 1+x\right ) ^{3/2}\left \vert y\left ( x\right ) +\sqrt {1+y\left ( x\right ) }\right \vert }=0\)
Maple
restart;
ode63:=diff(y(x),x)-(1+y(x)^2)/((1+x)^(3/2)*abs(y(x)+sqrt(1+y(x))))=0:
dsolve(%,y(x));
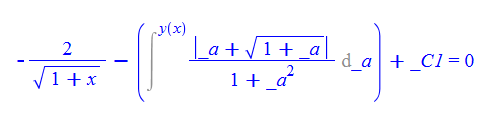
Mathematica
Remove["Global`*"];
ode63 = D[y[x],x]-(y[x]^2 + 1)/(Abs[y[x]+(1+y[x])^(1/2)]*(1+x)^(3/2))==0
DSolve[%, y[x], x] // TraditionalForm
No answer after 10 minutes wait
|
|
|
#64
\(y^{\prime }\left ( x\right ) -\sqrt {\frac {c+by\left ( x\right ) +ay\left ( x\right ) ^{2}}{c+bx+ax^{2}}}=0\)
Maple
restart;
ode64:=diff(y(x),x)-sqrt((c+b*y(x)+a*y(x)^2)/(c+b*x+a*x^2))=0:
dsolve(%,y(x));
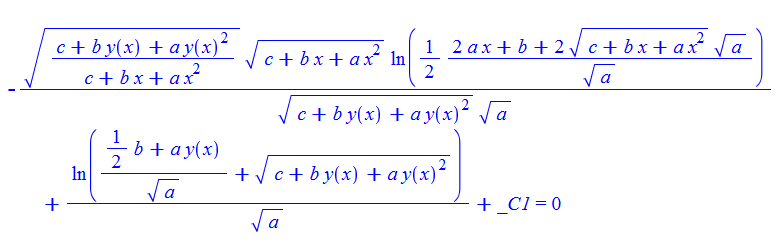
Mathematica
Clear["Global`*"];
ode64 =D[y[x], x] - ((a*y[x]^2 + b*y[x] + c)/(a*x^2 + b*x + c))^(1/2)==0
DSolve[%, y[x], x] // TraditionalForm
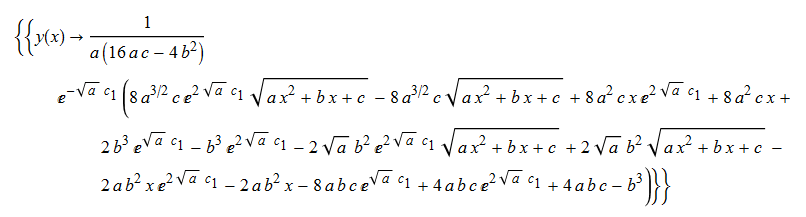
|
|
|
#65
\(y^{\prime }\left ( x\right ) -\sqrt {\frac {1+y\left ( x\right ) ^{3}}{1+x^{3}}}=0\)
Maple
restart;
ode65:=diff(y(x),x)-sqrt((1+y(x)^3)/(1+x^3))=0:
dsolve(%,y(x));
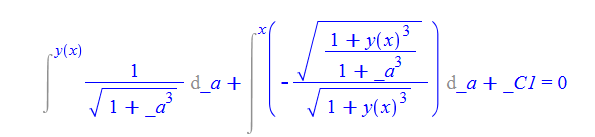
Mathematica
Clear["Global`*"];
ode65 = D[y[x], x] - ((y[x]^3 + 1)/(x^3 + 1))^(1/2) == 0
DSolve[%, y[x], x] // TraditionalForm

|
|
|
#66
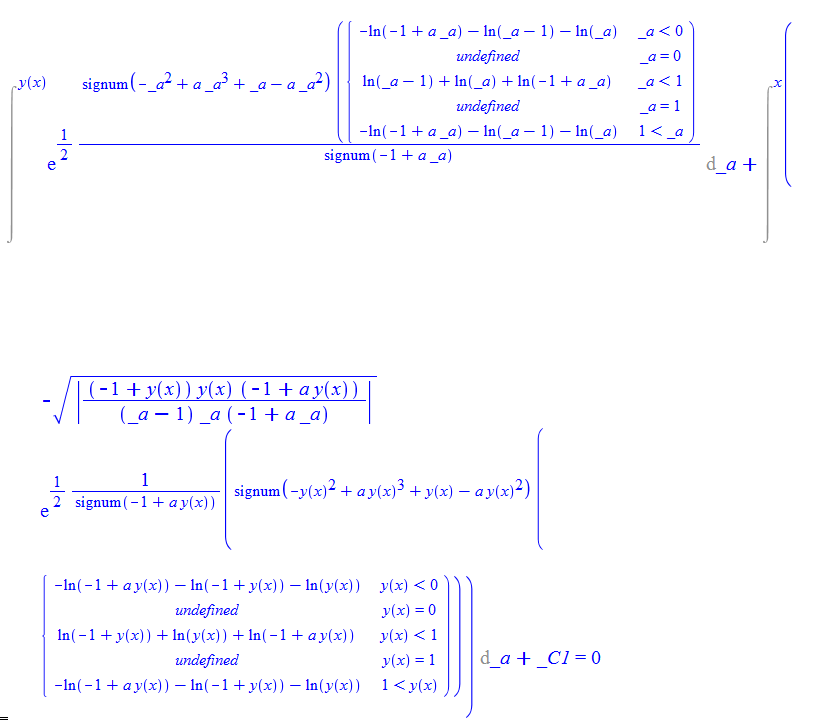
\(y^{\prime }\left ( x\right ) -\sqrt {\frac {\left \vert (1-y\left ( x\right ) )y\left ( x\right ) \left ( 1-ay\left ( x\right ) \right ) \right \vert }{\left \vert \left ( 1-x\right ) x\left ( 1-ax\right ) \right \vert }}=0\)
Maple
restart;
ode66:=diff(y(x),x)-sqrt((abs((1-y(x))*y(x)*(1-a*y(x))))/(abs((1-x)*x*(1-a*x))))=0:
dsolve(%,y(x));
Mathematica
Clear["Global`*"];
ode66=D[y[x],x]-Abs[y[x]*(1-y[x])*(1-a*y[x])]^(1/2)/Abs[x*(1-x)*(1-a*x)]^(1/2)==0
DSolve[%,y[x],x]//TraditionalForm
No answer after 10 minutes wait. Abort
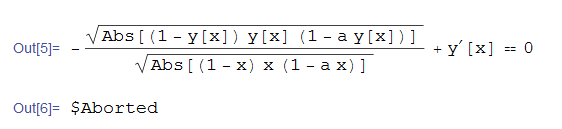 |
|
|
#67
\(y^{\prime }\left ( x\right ) -\sqrt {\frac {1+y\left ( x\right ) ^{4}}{1+x^{4}}}=0\)
Maple
restart;
ode67:=diff(y(x),x)-sqrt((1-y(x)^4)/(1-x^4))=0:
dsolve(%,y(x));
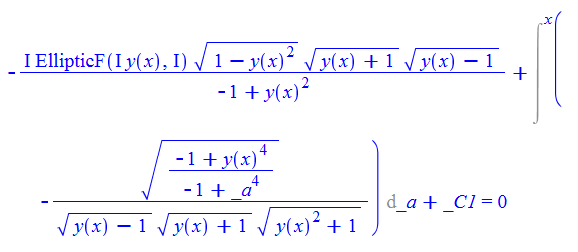
Mathematica
Clear["Global`*"];
ode67 = D[y[x], x] - (1 - y[x]^4)^(1/2)/(1 - x^4)^(1/2) == 0
DSolve[%, y[x], x] // TraditionalForm
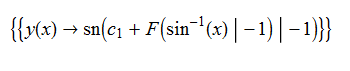
|
|
|
#68
\(y^{\prime }\left ( x\right ) -\sqrt {\frac {1+by\left ( x\right ) ^{2}+ay\left ( x\right ) ^{4}}{1+bx^{2}+ax^{4}}}=0\)
Maple
restart;
ode68:=diff(y(x),x)-sqrt((1+b*y(x)^2+a*y(x)^4)/(1+b*x^2+a*x^4))=0:
dsolve(%,y(x));
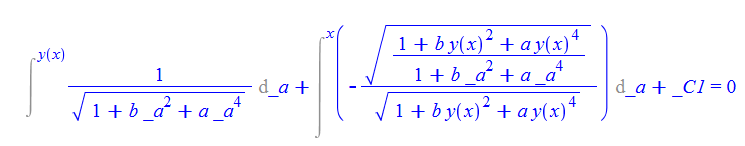
Mathematica
Clear["Global`*"];
ode68 = D[y[x],x]-((a*y[x]^4 + b*y[x]^2 + 1)/(a*x^4 + b*x^2 + 1))^(1/2) == 0
DSolve[%, y[x], x] // TraditionalForm
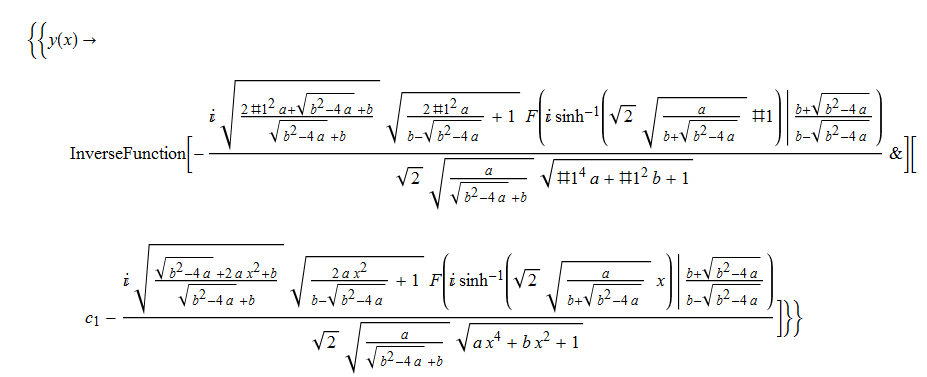
|
|
|
#69
\(y^{\prime }\left ( x\right ) -\sqrt {\left ( a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4}\right ) \left ( b_{0}+b_{1}y\left ( x\right ) +b_{2}y\left ( x\right ) ^{2}+b_{3}y\left ( x\right ) ^{3}+b_{4}y\left ( x\right ) ^{4}\right ) }=0\)
Maple
restart;
ode69:=diff(y(x),x)-sqrt((a0+a1*x+a2*x^2+a3*x^3+a4*x^4)*(b0+b1*y(x)+b2*y(x)^2+b3*y(x)^3+b4*y(x)^4))=0:
dsolve(%,y(x));
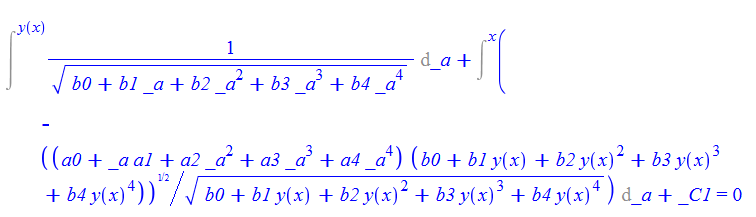
Mathematica
Clear["Global`*"];
ode69=D[y[x],x]-((b4*y[x]^4+b3*y[x]^3+b2*y[x]^2+b1*y[x]+b0)*
(a4*x^4+a3*x^3+a2*x^2+a1*x+a0))^(1/2)==0
DSolve[%,y[x],x]//TraditionalForm

|
|
|
#70
\(y^{\prime }\left ( x\right ) -\sqrt {\frac {a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4}}{b_{0}+b_{1}y\left ( x\right ) +b_{2}y\left ( x\right ) ^{2}+b_{3}y\left ( x\right ) ^{3}+b_{4}y\left ( x\right ) ^{4}}}=0\)
Maple
restart;
ode70:=diff(y(x),x)-sqrt((a0+a1*x+a2*x^2+a3*x^3+a4*x^4)/(b0+b1*y(x)+b2*y(x)^2+b3*y(x)^3+b4*y(x)^4))=0:
dsolve(%,y(x));
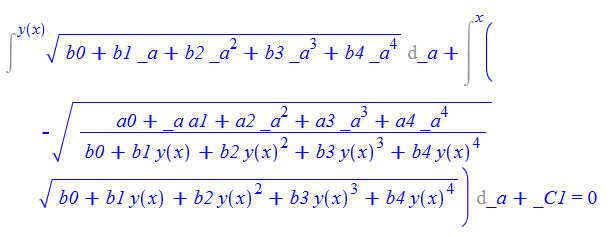
Mathematica
Clear["Global`*"];
ode70=D[y[x],x]-((a4*x^4 + a3*x^3 + a2*x^2 + a1*x + a0)/(b4*y[x]^4 +
b3*y[x]^3 + b2*y[x]^2 + b1*y[x] + b0))^(1/2) == 0
DSolve[%, y[x], x] // TraditionalForm

|
|
|
#71
\(y^{\prime }\left ( x\right ) -\sqrt {\frac {b_{0}+b_{1}y\left ( x\right ) +b_{2}y\left ( x\right ) ^{2}+b_{3}y\left ( x\right ) ^{3}+b_{4}y\left ( x\right ) ^{4}}{a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4}}}=0\)
Maple
restart;
ode71:=diff(y(x),x)-sqrt((b0+b1*y(x)+b2*y(x)^2+b3*y(x)^3+b4*y(x)^4)/(a0+a1*x+a2*x^2+a3*x^3+a4*x^4))=0;
dsolve(%,y(x));
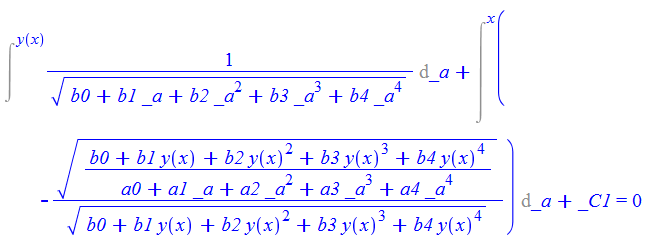
Mathematica
Clear["Global`*"];
ode71 = D[y[x],x] - ((b4*y[x]^4 + b3*y[x]^3 + b2*y[x]^2 + b1*y[x] + b0)/(a4*x^4 +
a3*x^3 + a2*x^2 + a1*x + a0))^(1/2) == 0
DSolve[%, y[x], x] // TraditionalForm

|
|
|
#72
\(y^{\prime }\left ( x\right ) -R_{1}\left ( x,\sqrt {a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4}}\right ) R_{2}\left ( y\left ( x\right ) ,\sqrt {b_{0}+b_{1}y\left ( x\right ) +b_{2}y\left ( x\right ) ^{2}+b_{3}y\left ( x\right ) ^{3}+b_{4}y\left ( x\right ) ^{4}}\right ) =0\)
Maple
restart;
ode72:=diff(y(x),x)-R1(x,sqrt(a0+a1*x+a2*x^2+a3*x^3+a4*x^4))*
R2(y(x),sqrt(b0+b1*y(x)+b2*y(x)^2+b3*y(x)^3+b4*y(x)^4))=0:
dsolve(%,y(x));
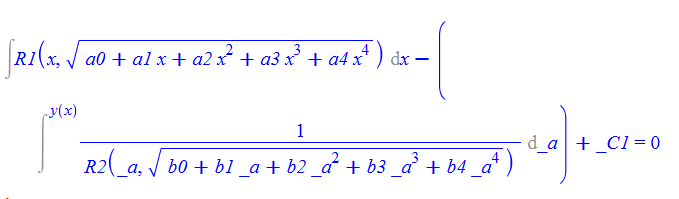
Mathematica
Clear["Global`*"];
ode72 = D[y[x], x] -R1[x, (a4*x^4 + a3*x^3 + a2*x^2 + a1*x + a0)^(1/2)]*
R2[y[x], (b4*y[x]^4 + b3*y[x]^3 + b2*y[x]^2 + b1*y[x] + b0)^(1/2)] == 0
DSolve[%, y[x], x] // TraditionalForm
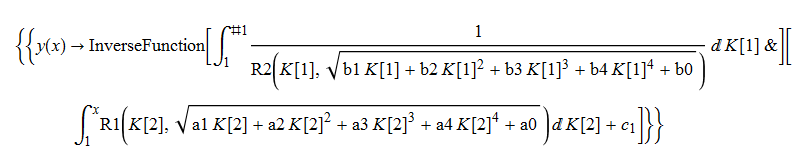
|
|
|
#73
\(y^{\prime }\left ( x\right ) -\left ( \frac {a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4}}{a_{0}+a_{1}y\left ( x\right ) +a_{2}y\left ( x\right ) ^{2}+a_{3}y\left ( x\right ) ^{3}}\right ) ^{\frac {2}{3}}=0\)
Maple
restart;
ode73:=diff(y(x),x)-((a0+a1*x+a2*x^2+a3*x^3)/(a0+a1*y(x)+a2*y(x)^2+a3*y(x)^3))^(2/3)=0;
dsolve(%,y(x));
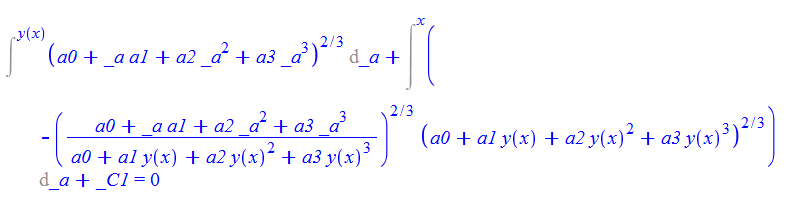
Mathematica
Clear["Global`*"];
ode73=D[y[x],x]-((a3*x^3+a2*x^2+a1*x+a0)/(a3*y[x]^3+a2*y[x]^2+a1*y[x]+a0))^(2/3)==0
DSolve[%,y[x],x]//TraditionalForm
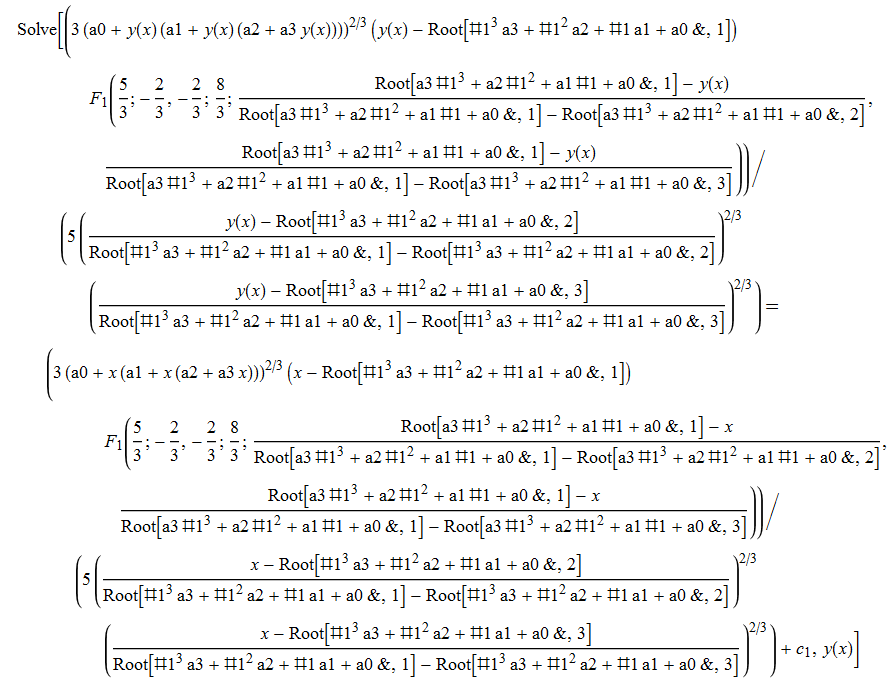
|
|
|
#74
\(y^{\prime }\left ( x\right ) -f\left ( x\right ) \sqrt {\left ( y\left ( x\right ) -a\right ) \left ( y\left ( x\right ) -b\right ) }\left ( y\left ( x\right ) -g\left ( x\right ) \right ) =0\)
Maple
restart;
ode74:=diff(y(x),x)-f(x)*sqrt((-a*y(x))*(-b*y(x)))*(y(x)-g(x))=0;
dsolve(%,y(x));
Not solved

Mathematica
Clear["Global`*"];
ode74 = D[y[x], x]-f[x]*(y[x] - g[x])*((y[x] - a)*(y[x] - b))^(1/2) == 0
DSolve[%, y[x], x] // TraditionalForm
Not solved
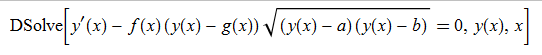 |
|
|
#75
\(y^{\prime }\left ( x\right ) +e^{x}-e^{x-y\left ( x\right ) }=0\)
Maple
restart;
ode75:=diff(y(x),x)+exp(x)-exp(x-y(x))=0;
dsolve(%,y(x));
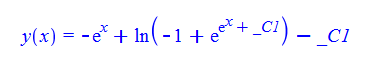
Mathematica
Clear["Global`*"];
ode75=D[y[x],x]-Exp[x-y[x]]+Exp[x]==0
DSolve[%,y[x],x]//TraditionalForm

|
|
|
#76
\(y^{\prime }\left ( x\right ) -b+a\ast \cos (y(x))=0\)
Maple
restart;
ode76:=diff(y(x),x)+b-a*cos(y(x))=0:
dsolve(%,y(x));
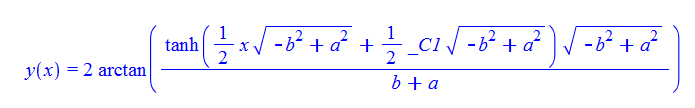
Mathematica
Clear["Global`*"];
ode76 = D[y[x], x] - a*Cos[y[x]] + b == 0
DSolve[%, y[x], x] // TraditionalForm

|
|
|
#77
\(y^{\prime }\left ( x\right ) -\cos \left ( bx+ay\left ( x\right ) \right ) =0\)
Maple
restart;
ode77:=diff(y(x),x)-cos(b*x+a*y(x))=0:
dsolve(%,y(x));
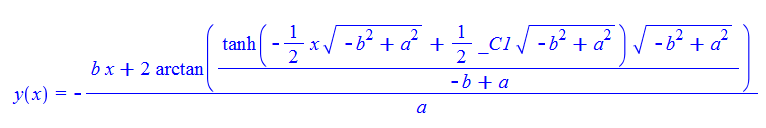
Mathematica
Clear["Global`*"];
ode77 = D[y[x], x] - Cos[a*y[x] + b*x] == 0
DSolve[%, y[x], x] // TraditionalForm

|
|
|
#78
\(y^{\prime }\left ( x\right ) +a\sin \left ( \alpha y\left ( x\right ) +\beta x\right ) +b=0\)
Maple
restart;
ode78:=diff(y(x),x)+a* sin(alpha *y(x)+ beta*x)+b=0:
dsolve(%,y(x));
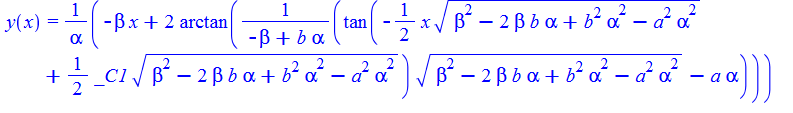
Mathematica
Clear["Global`*"];
ode78=D[y[x],x]+a*Sin[\[Alpha] y[x]+\[Beta]*x]+b==0
DSolve[%,y[x],x]//TraditionalForm

|
|
|
#79
\(y^{\prime }\left ( x\right ) +f\left ( x\right ) \cos \left ( ay\left ( x\right ) \right ) +g\left ( x\right ) \sin \left ( ay\left ( x\right ) \right ) +h\left ( x\right ) =0\)
Maple
restart;
ode79:=diff(y(x),x)+f(x)*cos(a*y(x))+g(x)*sin(a*y(x))+h(x)=0;
dsolve(%,y(x));
No solution
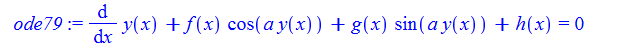
Mathematica
Clear["Global`*"];
ode79=D[y[x],x]+f[x]*Cos[a*y[x]]+g[x]*Sin[a*y[x]]+h[x]==0
DSolve[%,y[x],x]//TraditionalForm
No solution
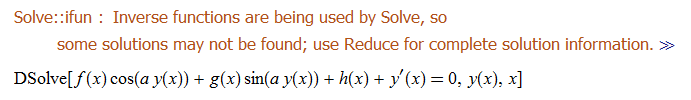 |
|
|
#80
\(y^{\prime }\left ( x\right ) +f\left ( x\right ) \sin \left ( y\left ( x\right ) \right ) +\left ( 1-f^{\prime }\left ( x\right ) \right ) \cos \left ( y\left ( x\right ) \right ) -f^{\prime }\left ( x\right ) -1=0\)
Maple
restart;
ode80:=diff(y(x),x)+f(x)*sin(y(x))+(1-diff(f(x),x))*cos(y(x))-diff(f(x),x)-1=0;
dsolve(%,y(x));
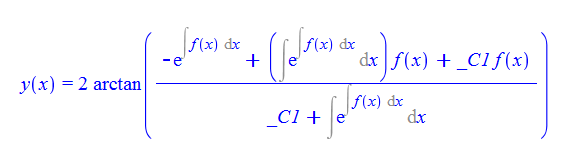
Mathematica
Clear["Global`*"];
ode80 = D[y[x], x] + f[x]*Sin[y[x]] + (1 - D[f[x], x])*Cos[y[x]] -
D[f[x], x] - 1 == 0
DSolve[%, y[x], x] // TraditionalForm
No solution
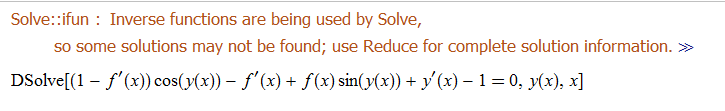 |
|
|
#81
\(y^{\prime }\left ( x\right ) +2\tan \left ( y\left ( x\right ) \right ) \tan \left ( x\right ) -1=0\)
Maple
restart;
ode81:=diff(y(x),x)+2*tan(y(x))*tan(x)-1=0;
dsolve(%,y(x));

Mathematica
Clear["Global`*"];
ode81 = D[y[x], x] + 2*Tan[y[x]]*Tan[x] - 1 == 0
DSolve[%, y[x], x] // TraditionalForm
No solution
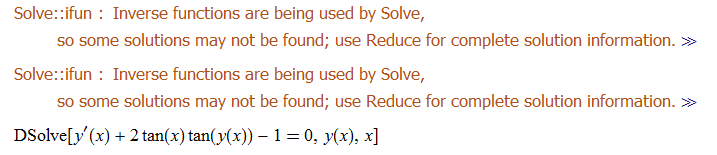 |
|
|
#82
\(y^{\prime }\left ( x\right ) -a\left ( 1+\tan \left ( y\left ( x\right ) \right ) ^{2}\right ) +\tan \left ( y\left ( x\right ) \right ) \tan \left ( x\right ) =0\)
Maple
restart;
ode82:=diff(y(x),x)-a*(1+tan(y(x))^2)+tan(y(x))*tan(x)=0;
dsolve(%,y(x));
No solution

Mathematica
Clear["Global`*"];
ode82 = D[y[x], x] - a*(1 + Tan[y[x]]^2) + Tan[y[x]]*Tan[x] == 0
DSolve[%, y[x], x] // TraditionalForm
No solution
 |
|
|
#83
\(y^{\prime }\left ( x\right ) -\tan \left ( xy\left ( x\right ) \right ) =0\)
Maple
restart;
ode83:=diff(y(x),x)-tan(x*y(x))=0;
dsolve(%,y(x));
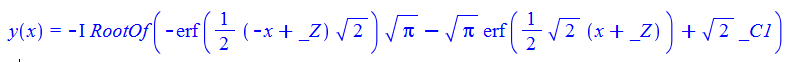
Mathematica
Clear["Global`*"];
ode83 = D[y[x], x] - Tan[x*y[x]] == 0
DSolve[%, y[x], x] // TraditionalForm
No solution
 |
|
|
#84
\(y^{\prime }\left ( x\right ) -f\left ( ax+by\left ( x\right ) \right ) =0\)
Maple
restart;
ode84:=diff(y(x),x)-f(a*x+b*y(x))=0:
dsolve(%,y(x));
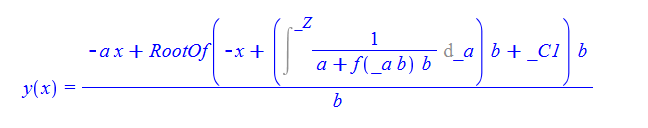
Mathematica
Clear["Global`*"];
ode84 = D[y[x], x] - f[a*x + b*y[x]] == 0
DSolve[%, y[x], x] // TraditionalForm
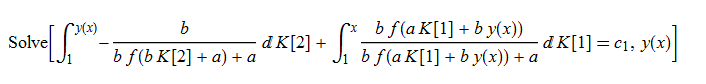
|
|
|
#85
\(y^{\prime }\left ( x\right ) -x^{a-1}f\left ( \frac {x^{a}}{a}+\frac {y\left ( x\right ) ^{b}}{b}\right ) y\left ( x\right ) ^{1-b}=0\)
Maple
restart;
ode85:=diff(y(x),x)-x^(a-1)*y(x)^(1-b)*f(x^a/a+y(x)^b/b)=0:
dsolve(%,y(x));
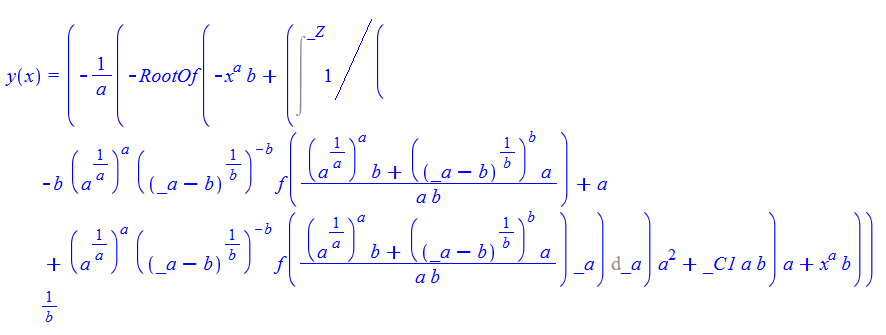
Mathematica
Clear["Global`*"];
ode85 = D[y[x], x] - x^(a - 1)*y[x]^(1 - b)*f[x^a/a + y[x]^b/b] == 0
DSolve[%, y[x], x] // TraditionalForm
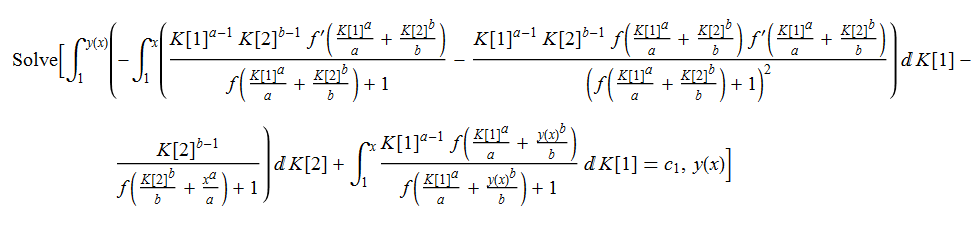
|
|
|
#86
\(y^{\prime }\left ( x\right ) -\frac {y\left ( x\right ) -xf\left ( x^{2}+ay\left ( x\right ) ^{2}\right ) }{x+af\left ( x^{2}+ay\left ( x\right ) ^{2}\right ) y\left ( x\right ) }=0\)
Maple
restart;
ode86:=diff(y(x),x)-((-x*f(x^2+a*y(x)^2)+y(x))/(x+a*f(x^2+a*y(x)^2)*y(x)))=0;
dsolve(%,y(x));
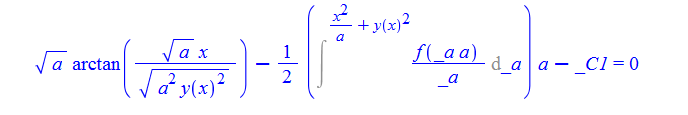
Mathematica
Clear["Global`*"];
ode86 = D[y[x],x]-(y[x]-x*f[x^2 + a*y[x]^2])/(x+a*y[x]*f[x^2+a*y[x]^2])==0
DSolve[%, y[x], x] // TraditionalForm
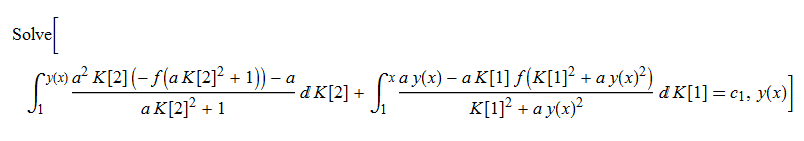
|
|
|
#87
\(y^{\prime }\left ( x\right ) -\frac {af\left ( x^{c}y\left ( x\right ) \right ) y\left ( x\right ) +cx^{a}y\left ( x\right ) ^{b}}{bxf\left ( x^{c}y\left ( x\right ) \right ) -x^{a}y\left ( x\right ) ^{b}}=0\)
Maple
restart;
ode87:=diff(y(x),x)-((a*f(x^c*y(x))*y(x)+c*x^a*y(x)^b)/(b*x*f(x^c*y(x))-x^a*y(x)^b))=0;
dsolve(%,y(x));
no solution
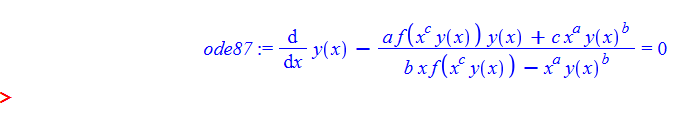
Mathematica
Clear["Global`*"];
ode87 = D[y[x],x]-(y[x]*a*f[x^c*y[x]]+c*x^a*y[x]^b)/(x*b*f[x^c*y[x]]-x^a*y[x]^b)== 0
DSolve[%, y[x], x] // TraditionalForm
no solution
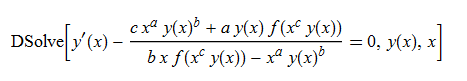 |
|
|
#88
\(2y^{\prime }\left ( x\right ) -b-ce^{-2ax}-4ay\left ( x\right ) -3y\left ( x\right ) ^{2}=0\)
Maple
restart;
ode88:=2*diff(y(x),x)-b-c*exp(-2*a*x)-4*a*y(x)-3*y(x)^2=0;
dsolve(%,y(x));
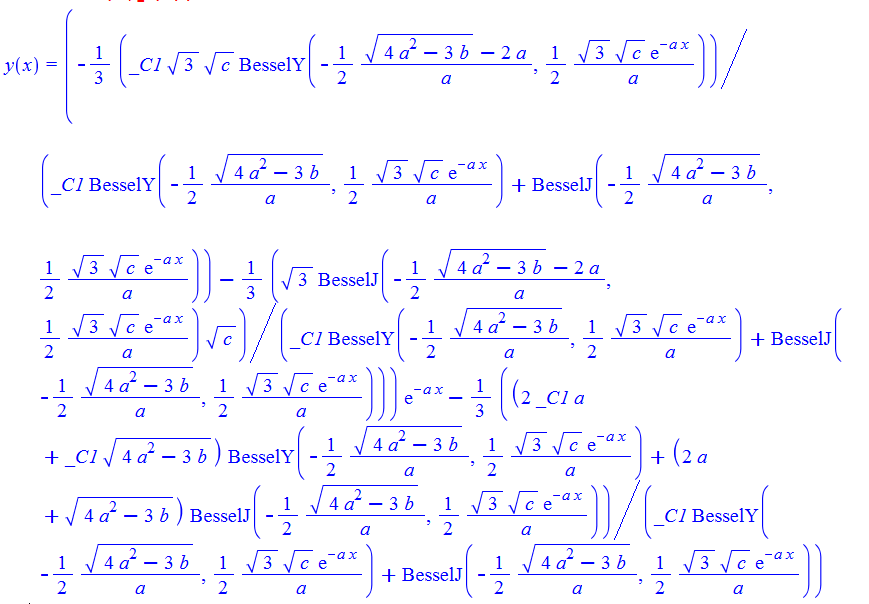
Mathematica
Clear["Global`*"];
ode88 = 2*D[y[x], x] - 3*y[x]^2 - 4*a*y[x] - b - c*Exp[-2*a*x] == 0
DSolve[%, y[x], x] // TraditionalForm

|
|
|
#89
\(xy^{\prime }\left ( x\right ) -\sqrt {a^{2}-x^{2}}=0\)
Maple
restart;
ode89:=x*diff(y(x),x)-sqrt(a^2-x^2)=0;
dsolve(%,y(x));
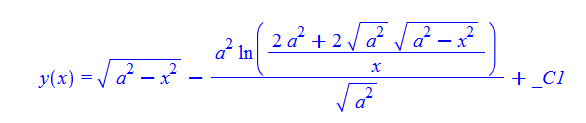
Mathematica
Clear["Global`*"];
ode89 = x*D[y[x], x] - (a^2 - x^2)^(1/2) == 0
DSolve[%, y[x], x] // TraditionalForm
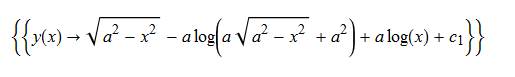
|
|
|
#90
\(xy^{\prime }\left ( x\right ) -x\sin \left ( x\right ) +y\left ( x\right ) =0\)
Maple
restart;
ode90:=x*diff(y(x),x)+y(x)-x*sin(x)=0:
dsolve(%,y(x));
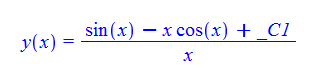
Mathematica
Clear["Global`*"];
ode90 = x*D[y[x], x] + y[x] - x*Sin[x] == 0
DSolve[%, y[x], x] // TraditionalForm
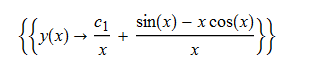
|
|
|
#91
\(xy^{\prime }\left ( x\right ) -y\left ( x\right ) -\frac {x}{\ln \left ( x\right ) }=0\)
Maple
restart;
ode91:=x*diff(y(x),x)-y(x)-x/log(x)=0:
dsolve(%,y(x));
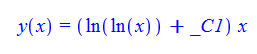
Mathematica
Clear["Global`*"];
ode91 = x*D[y[x], x] - y[x] - x/Log[x] == 0
DSolve[%, y[x], x] // TraditionalForm
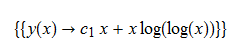
|
|
|
#92
\(xy^{\prime }\left ( x\right ) -y\left ( x\right ) -x^{2}\sin \left ( x\right ) =0\)
Maple
restart;
ode92:=x*diff(y(x),x)-y(x)-x^2*sin(x)=0:
dsolve(%,y(x));
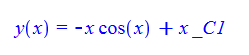
Mathematica
Clear["Global`*"];
ode92 = x*D[y[x], x] - y[x] - x^2*Sin[x] == 0
DSolve[%, y[x], x] // TraditionalForm
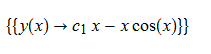
|
|
|
#93
\(xy^{\prime }\left ( x\right ) -y\left ( x\right ) -\frac {x\cos \left ( \ln \left ( \ln \left ( x\right ) \right ) \right ) }{\ln \left ( x\right ) }=0\)
Maple
restart;
ode93:=x*diff(y(x),x)-y(x)-(x*cos(log(log(x))))/(log(x))=0;
dsolve(%,y(x));
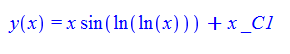
Mathematica
Clear["Global`*"];
ode93 = x*D[y[x], x] - y[x] - x*Cos[Log[Log[x]]]/Log[x] == 0
DSolve[%, y[x], x] // TraditionalForm
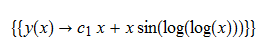
|
|
|
#94
\(xy^{\prime }\left ( x\right ) +bx^{n}+ay\left ( x\right ) =0\)
Maple
restart;
ode94:=x*diff(y(x),x)+b*x^n+a*y(x)=0:
dsolve(%,y(x));
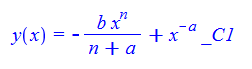
Mathematica
Clear["Global`*"];
ode94 = x*D[y[x], x] + a*y[x] + b*x^n == 0
DSolve[%, y[x], x] // TraditionalForm
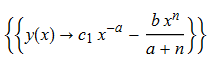
|
|
|
#95
\(xy^{\prime }\left ( x\right ) +x^{2}+y\left ( x\right ) ^{2}=0\)
Maple
restart;
ode95:=x*diff(y(x),x)+x^2+y(x)^2=0:
dsolve(%,y(x));
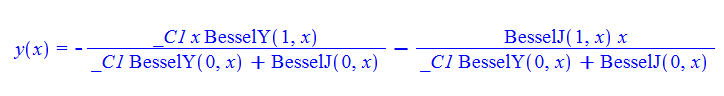
Mathematica
Clear["Global`*"];
ode95 = x*D[y[x], x] + y[x]^2 + x^2 == 0
DSolve[%, y[x], x] // TraditionalForm
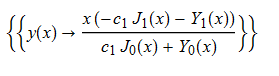
|
|
|
#96
\(xy^{\prime }\left ( x\right ) -y\left ( x\right ) ^{2}+1=0\)
Maple
restart;
ode96:=x*diff(y(x),x)+1-y(x)^2=0:
dsolve(%,y(x));
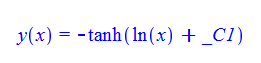
Mathematica
Clear["Global`*"];
ode96 = x*D[y[x], x] - y[x]^2 + 1 == 0
DSolve[%, y[x], x] // TraditionalForm
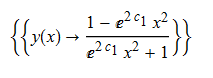
|
|
|
#97
\(xy^{\prime }\left ( x\right ) +bx^{2}-y\left ( x\right ) +ay\left ( x\right ) ^{2}=0\)
Maple
restart;
ode97:=x*diff(y(x),x)+b*x^2-y(x)+a*y(x)^2=0:
dsolve(%,y(x));
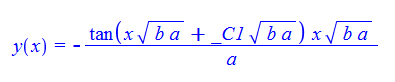
Mathematica
Clear["Global`*"];
ode97 = x*D[y[x], x] + a*y[x]^2 - y[x] + b*x^2 == 0
DSolve[%, y[x], x] // TraditionalForm
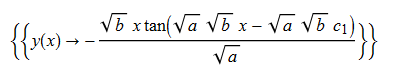
|
|
|
#98
\(xy^{\prime }\left ( x\right ) +cx^{2b}-by\left ( x\right ) +ay\left ( x\right ) ^{2}=0\)
Maple
restart;
ode98:=x*diff(y(x),x)+c*x^(2*b)-b*y(x)+a*y(x)^2=0;
dsolve(%,y(x));
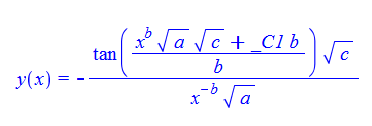
Mathematica
Clear["Global`*"];
ode98 = x*D[y[x], x] + a*y[x]^2 - b*y[x] + c*x^(2*b) == 0
DSolve[%, y[x], x] // TraditionalForm
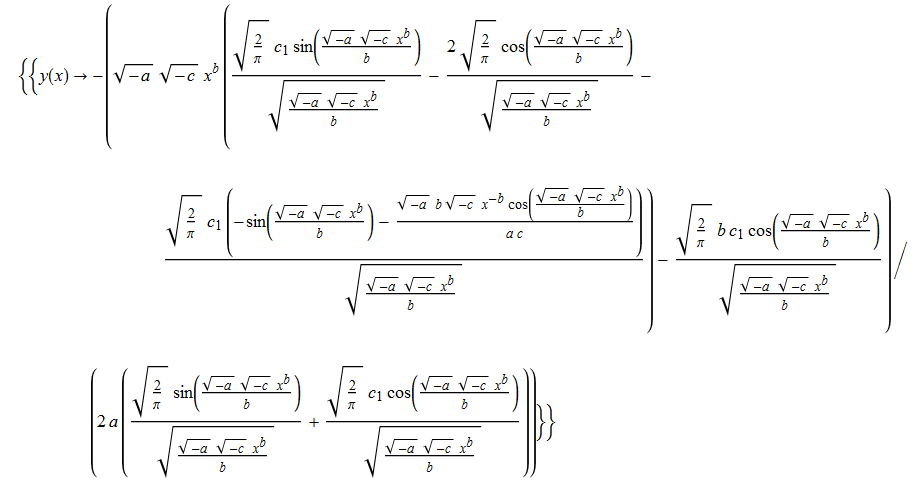
|
|
|
#99
\(xy^{\prime }\left ( x\right ) -cx^{\beta }-by\left ( x\right ) +ay\left ( x\right ) ^{2}=0\)
Maple
restart;
ode99:=x*diff(y(x),x)-c*x^beta-b*y(x)+a*y(x)^2=0;
dsolve(%,y(x));

Mathematica
Clear["Global`*"];
ode99 = x*D[y[x], x] + a*y[x]^2 - b*y[x] - c*x^\[Beta] == 0
DSolve[%, y[x], x] // TraditionalForm
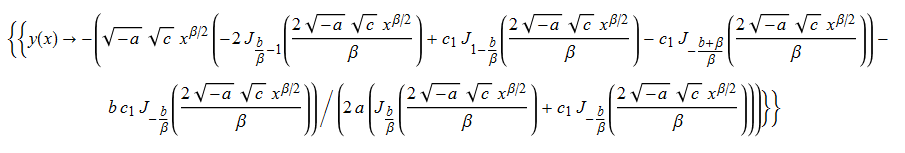
|
|
|
#100
\(xy^{\prime }\left ( x\right ) +a+xy\left ( x\right ) ^{2}=0\)
Maple
restart;
ode100:=x*diff(y(x),x)+a+x*y(x)^2=0:
dsolve(%,y(x));
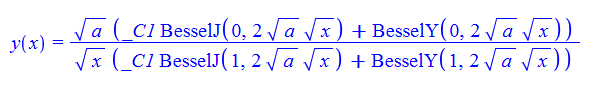
Mathematica
Clear["Global`*"];
ode100 = x*D[y[x], x] + x*y[x]^2 + a == 0
DSolve[%, y[x], x] // TraditionalForm
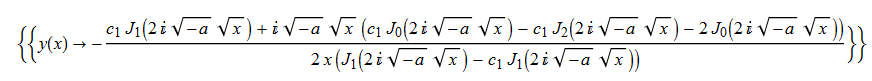
|
|
|
#101
\(xy^{\prime }\left ( x\right ) -y\left ( x\right ) +xy\left ( x\right ) ^{2}=0\)
Maple
restart;
ode101:=x*diff(y(x),x)-y(x)+x*y(x)^2=0:
dsolve(%,y(x));
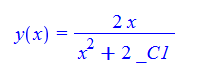
Mathematica
Clear["Global`*"];
ode101 = x*D[y[x], x] + x*y[x]^2 - y[x] == 0
DSolve[%, y[x], x] // TraditionalForm
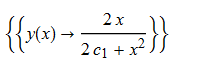
|
|
|
#102
\(xy^{\prime }\left ( x\right ) -ax^{3}-y\left ( x\right ) +xy\left ( x\right ) ^{2}=0\)
Maple
restart;
ode102:=x*diff(y(x),x)-a*x^3-y(x)+x*y(x)^2=0:
dsolve(%,y(x));
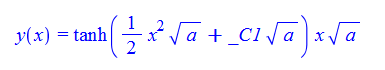
Mathematica
Clear["Global`*"];
ode102 = x*D[y[x], x] + x*y[x]^2 - y[x] - a*x^3 == 0
DSolve[%, y[x], x] // TraditionalForm
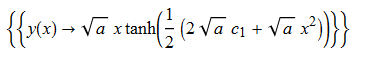
|
|
|
#103
\(xy^{\prime }\left ( x\right ) -x^{3}-\left ( 1+2x^{2}\right ) y\left ( x\right ) +xy\left ( x\right ) ^{2}=0\)
Maple
restart;
ode103:=x*diff(y(x),x)-x^3-(1+2*x^2)*y(x)+x*y(x)^2=0:
dsolve(%,y(x));
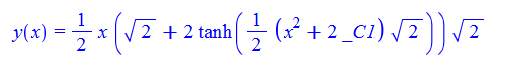
Mathematica
Clear["Global`*"];
ode103 = x*D[y[x], x] + x*y[x]^2 - (2*x^2 + 1)*y[x] - x^3 == 0
DSolve[%, y[x], x] // TraditionalForm
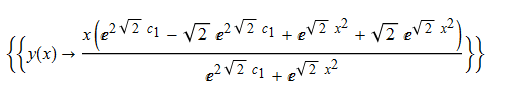
|
|
|
#104
\(xy^{\prime }\left ( x\right ) +bx+2y\left ( x\right ) +axy\left ( x\right ) ^{2}=0\)
Maple
restart;
ode104:=x*diff(y(x),x)+b*x+2*y(x)+a*x*y(x)^2=0:
dsolve(%,y(x));
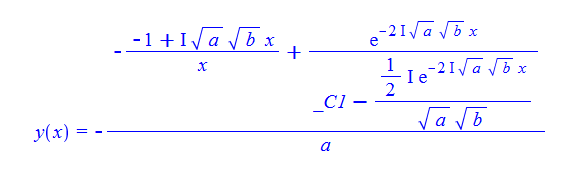
Mathematica
Clear["Global`*"];
ode104 = x*D[y[x], x] + a*x*y[x]^2 + 2*y[x] + b*x == 0
DSolve[%, y[x], x] // TraditionalForm
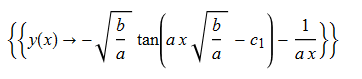
|
|
|
#105
\(xy^{\prime }\left ( x\right ) +d+cx+by\left ( x\right ) +axy\left ( x\right ) ^{2}=0\)
Maple
restart;
ode105:=x*diff(y(x),x)+d+c*x+b*y(x)+a*x*y(x)^2=0:
dsolve(%,y(x));
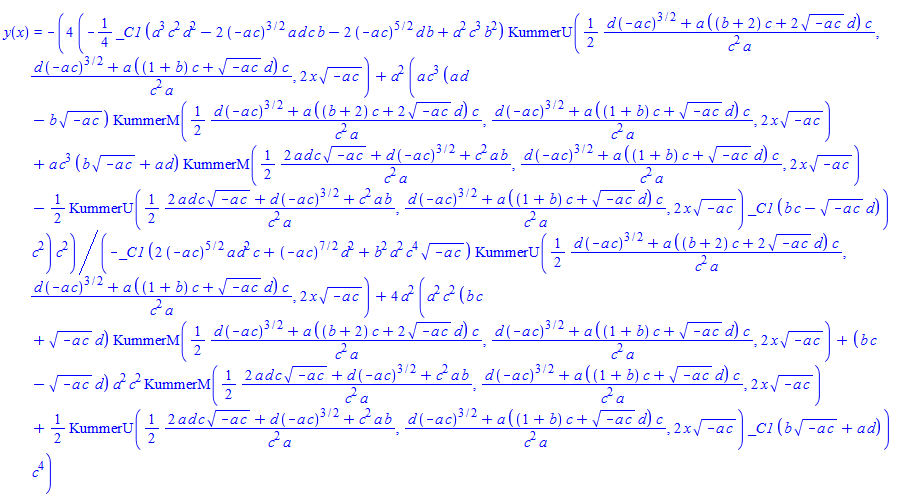
Mathematica
Clear["Global`*"];
ode105 = x*D[y[x], x] + a*x*y[x]^2 + b*y[x] + c*x + d == 0
DSolve[%, y[x], x] // TraditionalForm
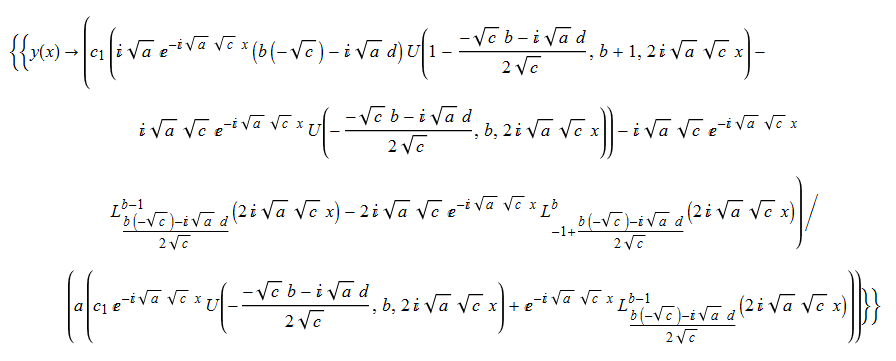
|
|
|
#106
\(xy^{\prime }\left ( x\right ) +x^{b}+\frac {1}{2}\left ( a-b\right ) y\left ( x\right ) +x^{a}y\left ( x\right ) ^{2}=0\)
Maple
restart;
ode106:=x*diff(y(x),x)+x^b+(1/2)*(a-b)*y(x)+x^a*y(x)^2=0:
dsolve(%,y(x));
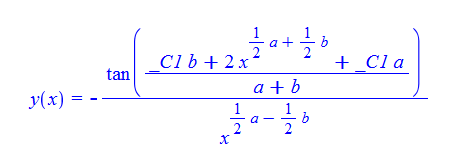
Mathematica
Clear["Global`*"];
ode106 = x*D[y[x], x] + x^a*y[x]^2 + 1/2*(a - b)*y[x] + x^b == 0
DSolve[%, y[x], x] // TraditionalForm
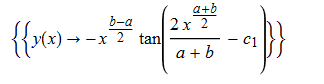
|
|
|
#107
\(xy^{\prime }\left ( x\right ) -cx^{\beta }+by\left ( x\right ) +ax^{\alpha }y\left ( x\right ) ^{2}=0\)
Maple
restart;
ode107:=x*diff(y(x),x)-c*x^beta+b*y(x)+a*x^alpha*y(x)^2=0:
dsolve(%,y(x));
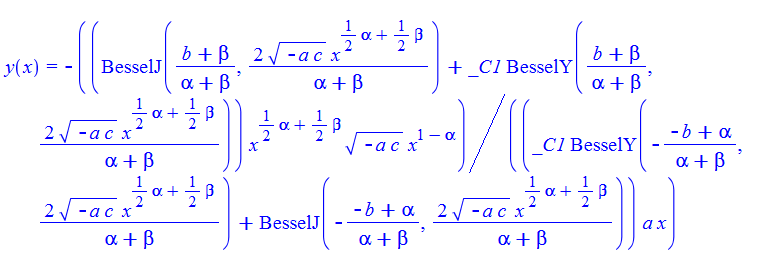
Mathematica
Clear["Global`*"];
ode107 = x*D[y[x], x] + a*x^\[Alpha]*y[x]^2 + b*y[x] - c*x^\[Beta] == 0
DSolve[%, y[x], x] // TraditionalForm

|
|
|
#108
\(xy^{\prime }\left ( x\right ) -y\left ( x\right ) ^{2}\ln \left ( x\right ) +y\left ( x\right ) =0\)
Maple
restart;
ode108:=x*diff(y(x),x)-y(x)^2*log(x)+y(x)=0;
dsolve(%,y(x));
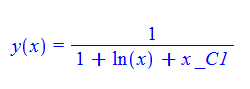
Mathematica
Clear["Global`*"];
ode108 = x*D[y[x], x] - y[x]^2*Log[x] + y[x] == 0
DSolve[%, y[x], x] // TraditionalForm
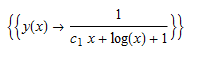
|
|
|
#109
\(xy^{\prime }\left ( x\right ) -y\left ( x\right ) \left ( 2y\left ( x\right ) \ln \left ( x\right ) -1\right ) =0\)
Maple
restart;
ode109:=x*diff(y(x),x)-y(x)*(2*log(x)*y(x)-1)=0:
dsolve(%,y(x));
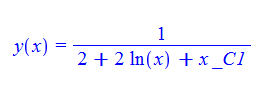
Mathematica
Clear["Global`*"];
ode109 = x*D[y[x], x] - y[x]*(2*y[x]*Log[x] - 1) == 0
DSolve[%, y[x], x] // TraditionalForm
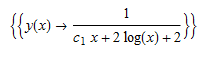
|
|
|
#110
\(xy^{\prime }\left ( x\right ) -f\left ( x\right ) \left ( y\left ( x\right ) ^{2}-x^{2}\right ) =0\)
Maple
restart;
ode110:=x*diff(y(x),x)-f(x)*(y(x)^2-x^2)=0:
dsolve(%,y(x));
did not solve
Mathematica
Clear["Global`*"];
ode110 = x*D[y[x], x] + f[x]*(y[x]^2 - x^2) == 0
DSolve[%, y[x], x] // TraditionalForm
did not solve |
|
|
#111
\(xy^{\prime }\left ( x\right ) +y\left ( x\right ) ^{3}+3xy\left ( x\right ) ^{2}=0\)
Maple
restart;
ode111:=x*diff(y(x),x)+y(x)^3+3*x*y(x)^2=0;
dsolve(%,y(x));
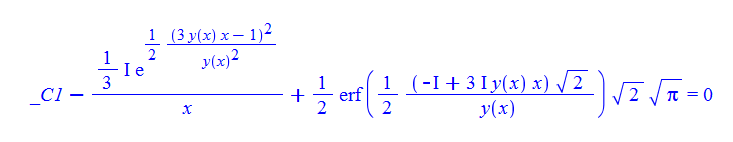
Mathematica
Clear["Global`*"];
ode111 = x*D[y[x], x] + y[x]^3 + 3*x*y[x]^2 == 0
DSolve[%, y[x], x] // TraditionalForm
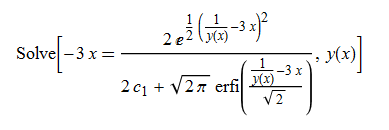
|
|
|
#112
\(xy^{\prime }\left ( x\right ) -y(x)-\sqrt {x^{2}+y\left ( x\right ) ^{2}}=0\)
Maple
restart;
ode112:=x*diff(y(x),x)-y(x)-sqrt(x^2+y(x)^2)=0:
dsolve(%,y(x));
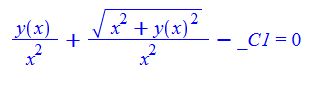
Mathematica
Clear["Global`*"];
ode112 = x*D[y[x], x] - (y[x]^2 + x^2)^(1/2) - y[x] == 0
DSolve[%, y[x], x] // TraditionalForm
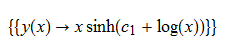
|
|
|
#113
\(xy^{\prime }\left ( x\right ) -y(x)+a\sqrt {x^{2}+y\left ( x\right ) ^{2}}=0\)
Maple
restart;
ode113:=x*diff(y(x),x)-y(x)+a*sqrt(x^2+y(x)^2):
dsolve(%,y(x));
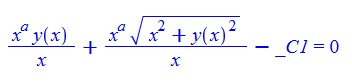
Mathematica
Clear["Global`*"];
ode113 = x*D[y[x], x] + a*(y[x]^2 + x^2)^(1/2) - y[x] == 0
DSolve[%, y[x], x]
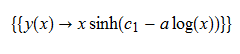
|
|
|
#114
\(xy^{\prime }\left ( x\right ) -y(x)-x\sqrt {x^{2}+y\left ( x\right ) ^{2}}=0\)
Maple
restart;
ode114:=x*diff(y(x),x)-x*sqrt(y(x)^2+x^2)-y(x)=0:
dsolve(%,y(x));
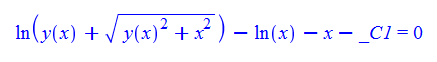
Mathematica
Clear["Global`*"];
ode114 = x*D[y[x], x] - x*(y[x]^2 + x^2)^(1/2) - y[x] == 0
DSolve[%, y[x], x] // TraditionalForm
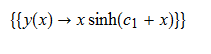
|
|
|
#115
\(xy^{\prime }\left ( x\right ) -y\left ( x\right ) -x\left ( y\left ( x\right ) -x\right ) \sqrt {x^{2}+y\left ( x\right ) ^{2}}=0\)
Maple
restart;
ode115:=x*diff(y(x),x)-y(x)-x*(y(x)-x)*sqrt(x^2+y(x)^2)=0:
dsolve(%,y(x));
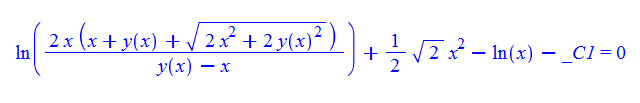
Mathematica
Clear["Global`*"];
ode115 = x*D[y[x], x] - x*(y[x] - x)*(y[x]^2 + x^2)^(1/2) - y[x] == 0
DSolve[%, y[x], x] // TraditionalForm
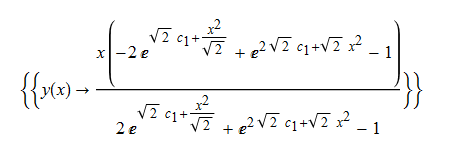
|
|
|
#116
\(xy^{\prime }\left ( x\right ) -y\left ( x\right ) -x\sqrt {\left ( y\left ( x\right ) ^{2}-4x^{2}\right ) \left ( y\left ( x\right ) ^{2}-x^{2}\right ) }=0\)
Maple
restart;
ode116:=x*diff(y(x),x)-y(x)-x*sqrt((y(x)^2-4*x^2)*(y(x)^2-x^2))=0:
dsolve(%,y(x));
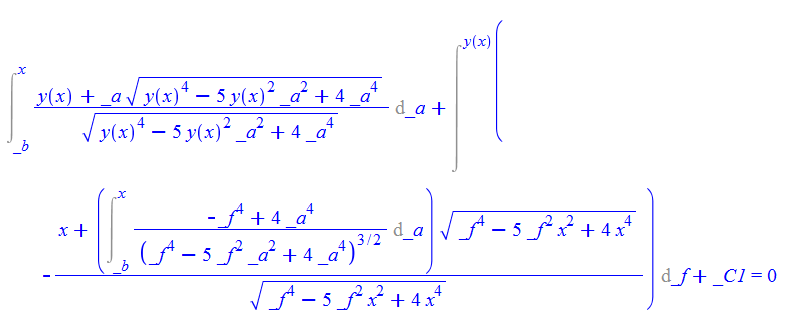
Mathematica
Clear["Global`*"];
ode116 = x*D[y[x], x]-x*((y[x]^2 - x^2)*(y[x]^2-4*x^2))^(1/2)-y[x] == 0
DSolve[%, y[x], x] // TraditionalForm
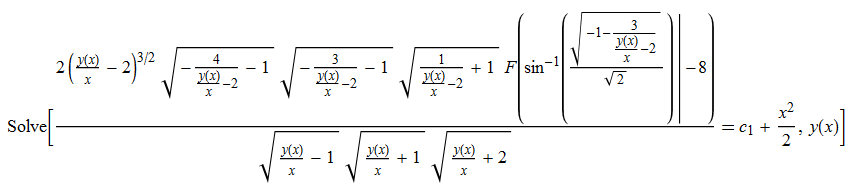
|
|
|
#117
\(xy^{\prime }\left ( x\right ) -x-xe^{\frac {y\left ( x\right ) }{x}}-y\left ( x\right ) =0\)
Maple
restart;
ode117:=x*diff(y(x),x)-x-x*exp(y(x)/x)-y(x)=0:
dsolve(%,y(x));
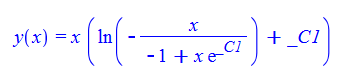
Mathematica
Clear["Global`*"];
ode117 = x*D[y[x], x] - x*Exp[y[x]/x] - y[x] - x == 0
DSolve[%, y[x], x] // TraditionalForm

|
|
|
#118
\(xy^{\prime }\left ( x\right ) -y\left ( x\right ) \ln \left ( y\left ( x\right ) \right ) =0\)
Maple
restart;
ode118:=x*diff(y(x),x)-y(x)*log(y(x))=0;
dsolve(%,y(x));
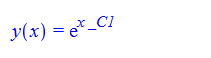
Mathematica
Clear["Global`*"];
ode118 = x*D[y[x], x] - y[x]*Log[y[x]] == 0
DSolve[%, y[x], x] // TraditionalForm
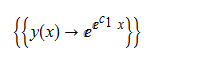
|
|
|
#119
\(xy^{\prime }\left ( x\right ) -y\left ( x\right ) \left ( \ln \left ( xy\left ( x\right ) \right ) -1\right ) =0\)
Maple
restart;
ode119:=x*diff(y(x),x)-y(x)*(log(x*y(x))-1)=0:
dsolve(%,y(x));
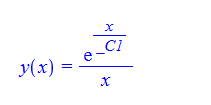
Mathematica
Clear["Global`*"];
ode119 = x*D[y[x], x] - y[x]*(Log[x*y[x]] - 1) == 0
DSolve[%, y[x], x] // TraditionalForm
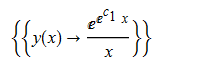
|
|
|
#120
\(xy^{\prime }\left ( x\right ) -y\left ( x\right ) \left ( 2+x\ln \left ( \frac {x^{2}}{y\left ( x\right ) }\right ) \right ) =0\)
Maple
restart;
ode120:=x*diff(y(x),x)-y(x)*(2+x*log(x^2/y(x)))=0:
dsolve(%,y(x));
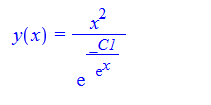
Mathematica
Clear["Global`*"];
ode120 = x*D[y[x], x] - y[x]*(x*Log[x^2/y[x]] + 2) == 0
DSolve[%, y[x], x] // TraditionalForm
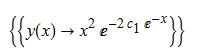
|
|
|
#121
\(xy^{\prime }\left ( x\right ) +\sin \left ( y\left ( x\right ) -x\right ) =0\)
Maple
restart;
ode121:=x*diff(y(x),x)+sin(y(x)-x)=0;
dsolve(%,y(x));
Did not solve
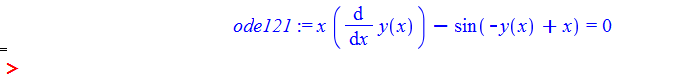
Mathematica
Clear["Global`*"];
ode121 = x*D[y[x], x] + Sin[y[x] - x] == 0
DSolve[%, y[x], x] // TraditionalForm
Did not solve
 |
|
|
#122
\(xy^{\prime }\left ( x\right ) +\cos \left ( y\left ( x\right ) \right ) \left ( \sin \left ( y\left ( x\right ) \right ) -3x^{2}\cos \left ( y\left ( x\right ) \right ) \right ) =0\)
Maple
restart;
ode122:=x*diff(y(x),x)+cos(y(x))*(sin(y(x))-3*x^2*cos(y(x)))=0:
dsolve(%,y(x));
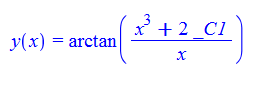
Mathematica
Clear["Global`*"];
ode122 = x*D[y[x], x] + (Sin[y[x]] - 3*x^2*Cos[y[x]])*Cos[y[x]] == 0
DSolve[%, y[x], x] // TraditionalForm

|
|
|
#123
\(xy^{\prime }\left ( x\right ) -x\sin \left ( \frac {y\left ( x\right ) }{x}\right ) -y\left ( x\right ) =0\)
Maple
restart;
ode123:=x*diff(y(x),x)-y(x)-x*sin(y(x)/x)=0:
dsolve(%,y(x));
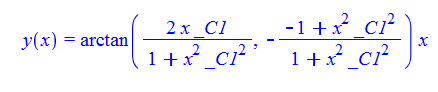
Mathematica
Clear["Global`*"];
ode123 = x*D[y[x], x] - x*Sin[y[x]/x] - y[x] == 0
DSolve[%, y[x], x] // TraditionalForm

|
|
|
#124
\(xy^{\prime }\left ( x\right ) +x\cos \left ( \frac {y\left ( x\right ) }{x}\right ) -y\left ( x\right ) +x=0\)
Maple
restart;
ode124:=x*diff(y(x),x)+x*cos(y(x)/x)-y(x)+x=0;
dsolve(%,y(x));

Mathematica
Clear["Global`*"];
ode124 = x*D[y[x], x] + x*Cos[y[x]/x] - y[x] + x == 0
DSolve[%, y[x], x] // TraditionalForm

|
|
|
#125
\(xy^{\prime }\left ( x\right ) +x\tan \left ( \frac {y\left ( x\right ) }{x}\right ) -y\left ( x\right ) =0\)
Maple
restart;
ode125:=x*diff(y(x),x)+x*tan(y(x)/x)-y(x)=0:
dsolve(%,y(x));
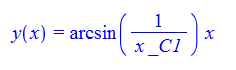
Mathematica
Clear["Global`*"];
ode125 = x*D[y[x], x] + x*Tan[y[x]/x] - y[x] == 0
DSolve[%, y[x], x] // TraditionalForm

|
|
|
#126 \(xy^{\prime }\left ( x\right ) -y\left ( x\right ) f\left ( xy\left ( x\right ) \right ) =0\)
Maple
restart;
ode126:=x*diff(y(x),x)-y(x)*f(x*y(x))=0:
dsolve(%,y(x));
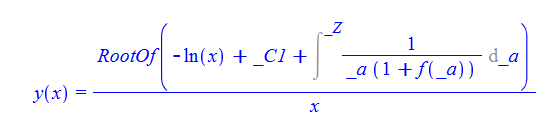
Mathematica
Clear["Global`*"];
ode126 = x*D[y[x], x] - y[x]*f[x*y[x]] == 0
DSolve[%, y[x], x] // TraditionalForm
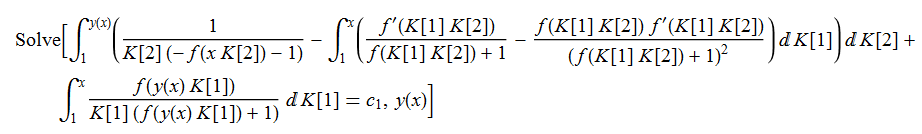
|
|
|
#127
\(xy^{\prime }\left ( x\right ) -y\left ( x\right ) f\left ( x^{a}y\left ( x\right ) ^{b}\right ) =0\)
Maple
restart;
ode127:=x*diff(y(x),x)-f(x^a*y(x)^b)*y(x)=0;
dsolve(%,y(x));
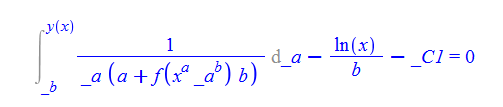
Mathematica
Clear["Global`*"];
ode127 = x*D[y[x], x] - y[x]*f[x^a*y[x]^b] == 0
DSolve[%, y[x], x] // TraditionalForm
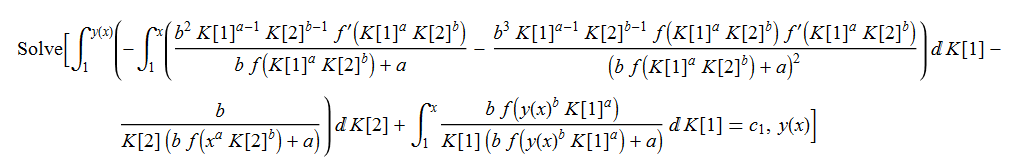
|
|
|
#128
\(xy^{\prime }\left ( x\right ) -f\left ( x\right ) g\left ( x^{a}y\left ( x\right ) \right ) +ay\left ( x\right ) =0\)
Maple
restart;
ode128:=x*diff(y(x),x)-f(x)*g(x^a*y(x))+a*y(x)=0:
dsolve(%,y(x));
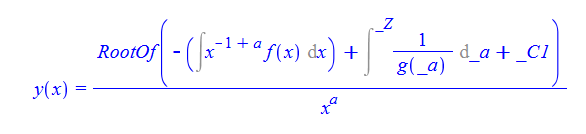
Mathematica
Clear["Global`*"];
ode128 = x*D[y[x], x] + a*y[x] - f[x]*g[x^a*y[x]] == 0
DSolve[%, y[x], x] // TraditionalForm
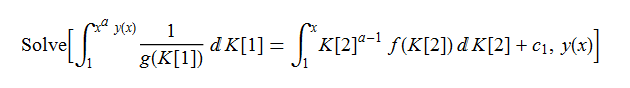
|
|
|
#129
\(\left ( 1+x\right ) y^{\prime }\left ( x\right ) +y\left ( x\right ) \left ( y\left ( x\right ) -x\right ) =0\)
Maple
restart;
ode129:=(1+x)*diff(y(x),x)+y(x)*(y(x)-x)=0:
dsolve(%,y(x));
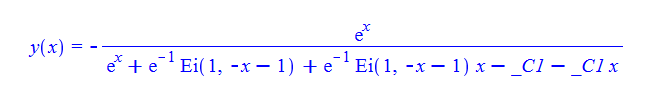
Mathematica
Clear["Global`*"];
ode129 = (1 + x)*D[y[x], x] + y[x]*(y[x] - x) == 0
DSolve[%, y[x], x] // TraditionalForm
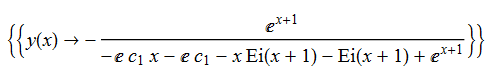
|
|
|
#130
\(2xy^{\prime }\left ( x\right ) -2x^{3}-y\left ( x\right ) =0\)
Maple
restart;
ode130:=2*x*diff(y(x),x)-2*x^3-y(x)=0:
dsolve(%,y(x));
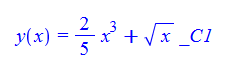
Mathematica
Clear["Global`*"];
ode130 = 2*x*D[y[x], x] - y[x] - 2*x^3 == 0
DSolve[%, y[x], x] // TraditionalForm
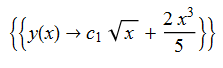
|
|
|
#131
\(\left ( 1+2x\right ) y^{\prime }\left ( x\right ) +2-4e^{-y\left ( x\right ) }=0\)
Maple
restart;
ode131:=(1+2*x)*diff(y(x),x)+2-4*exp(-y(x))=0:
dsolve(%,y(x));
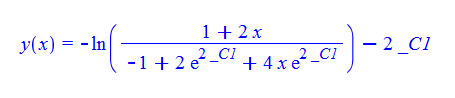
Mathematica
Clear["Global`*"];
ode131 = (2*x + 1)*D[y[x], x] - 4*Exp[-y[x]] + 2 == 0
DSolve[%, y[x], x] // TraditionalForm

|
|
|
#132
\(3xy^{\prime }\left ( x\right ) -y\left ( x\right ) -3x\log \left ( x\right ) y\left ( x\right ) ^{4}=0\)
Maple
restart;
ode132:=3*x*diff(y(x),x)-y(x)-3*x*log(x)*y(x)^4=0:
dsolve(%,y(x));
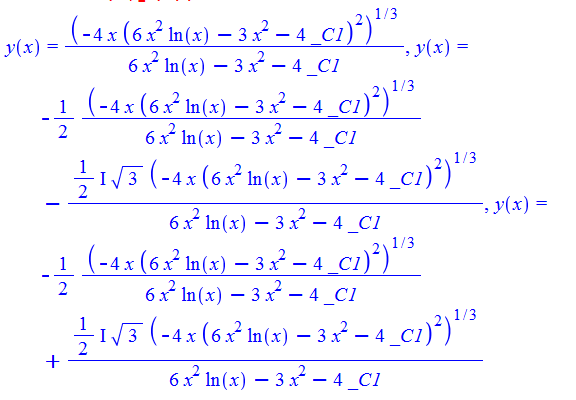
Mathematica
Clear["Global`*"];
ode132 = 3*x*D[y[x], x] - 3*x*Log[x]*y[x]^4 - y[x] == 0
DSolve[%, y[x], x] // TraditionalForm
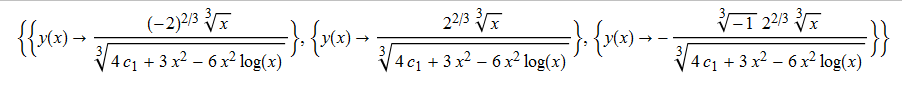
|
|
|
#133
\(x^{2}y^{\prime }\left ( x\right ) +y\left ( x\right ) =x\)
Maple
restart;
ode133:=x^2*diff(y(x),x)+y(x)=x:
dsolve(%,y(x));
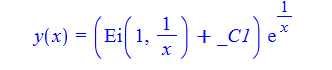
Mathematica
Clear["Global`*"];
ode133 = x^2*D[y[x], x] + y[x] == x
DSolve[%, y[x], x] // TraditionalForm
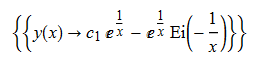
|
|
|
#134
\(x^{2}y^{\prime }\left ( x\right ) -y\left ( x\right ) =-x^{2}e^{\left ( x-\frac {1}{x}\right ) }\)
Maple
restart;
ode134:=x^2*diff(y(x),x)-y(x)=-x^2*exp(x - 1/x):
dsolve(%,y(x));
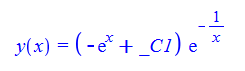
Mathematica
Clear["Global`*"];
ode134 = x^2*D[y[x], x] - y[x] == -x^2*Exp[x - 1/x]
DSolve[%, y[x], x] // TraditionalForm
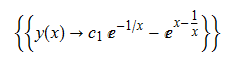
|
|
|
#135
\(x^{2}y^{\prime }\left ( x\right ) -\left ( x-1\right ) y\left ( x\right ) =0\)
Maple
restart;
ode135:=x^2*diff(y(x),x)-(x-1)*y(x)=0:
dsolve(%,y(x));
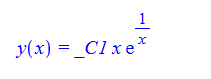
Mathematica
Clear["Global`*"];
ode135 = x^2*D[y[x], x] - (-1 + x)*y[x] == 0
DSolve[%, y[x], x] // TraditionalForm
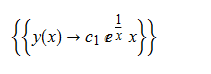
|
|
|
#136
\(x^{2}y^{\prime }\left ( x\right ) +xy\left ( x\right ) +y\left ( x\right ) ^{2}=-x^{2}\)
Maple
restart;
ode136:=x^2*diff(y(x),x)+x*y(x)+y(x)^2=-x^2:
dsolve(%,y(x));
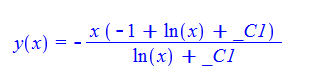
Mathematica
Clear["Global`*"];
ode136 = x^2*D[y[x], x] + y[x]^2 + x*y[x] == -x^2
DSolve[%, y[x], x] // TraditionalForm
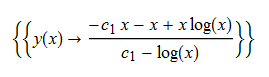
|
|
|
#137
\(x^{2}y^{\prime }\left ( x\right ) -xy\left ( x\right ) -y\left ( x\right ) ^{2}=0\)
Maple
restart;
ode137:=x^2*diff(y(x),x)-y(x)^2-x*y(x)=0:
dsolve(%,y(x));
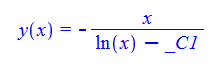
Mathematica
Clear["Global`*"];
ode137 = x^2*D[y[x], x] - y[x]^2 - x*y[x] == 0
DSolve[%, y[x], x] // TraditionalForm
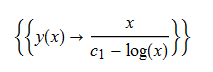
|
|
|
#138 \(x^{2}y^{\prime }\left ( x\right ) -xy\left ( x\right ) -y\left ( x\right ) ^{2}=x^{2}\)
Maple
restart;
ode138:=x^2*diff(y(x),x)-y(x)^2-x*y(x)=x^2:
dsolve(%,y(x));
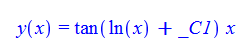
Mathematica
Clear["Global`*"];
ode138 = x^2*D[y[x], x] - y[x]^2 - x*y[x] == x^2
DSolve[%, y[x], x] // TraditionalForm
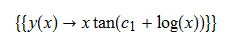
|
|
|
#139 \(x^{2}(y^{\prime }\left ( x\right ) +y\left ( x\right ) ^{2})=-ax^{k}+b\left ( b-1\right ) \)
Maple
restart;
ode139:=x^2*(y(x)^2+diff(y(x),x))=-a*x^k+b*(b-1):
dsolve(%,y(x));
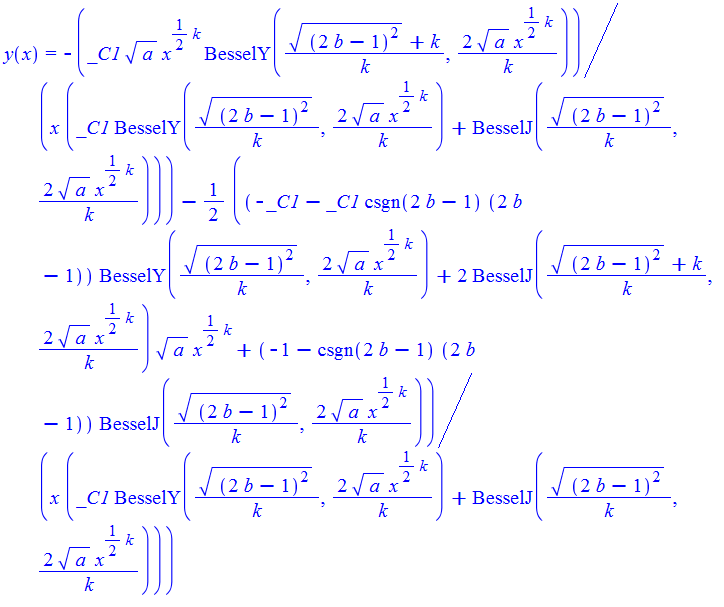
Mathematica
Clear["Global`*"];
ode139 = x^2*(D[y[x], x] + y[x]^2) == -a*x^k + b*(b - 1)
DSolve[%, y[x], x] // TraditionalForm
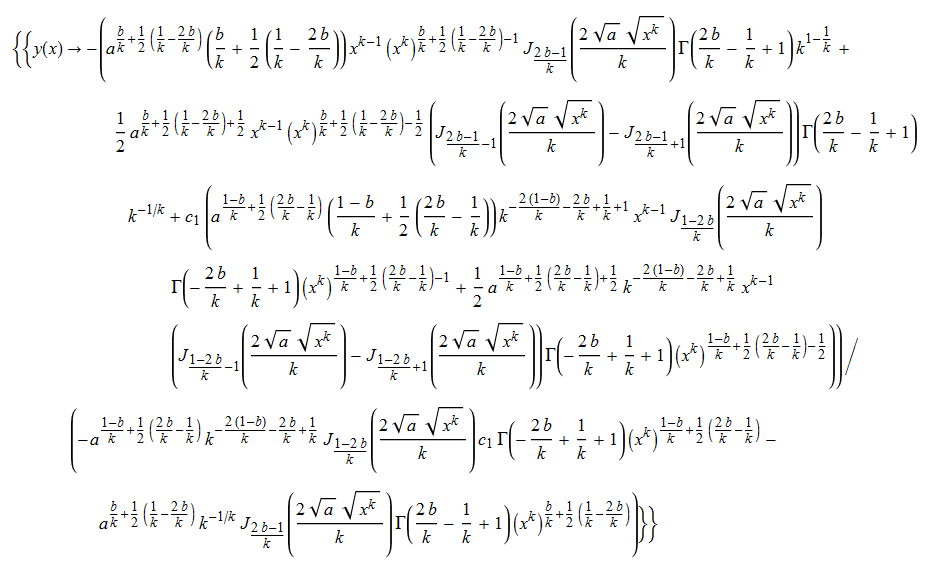
|
|
|
#140 \(x^{2}(y^{\prime }\left ( x\right ) +y\left ( x\right ) ^{2})=-4xy\left ( x\right ) -2\)
Maple
restart;
ode140:=x^2*(y(x)^2+diff(y(x),x))=-4*x*y(x)-2:
dsolve(%,y(x));
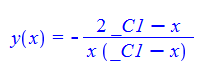
Mathematica
Clear["Global`*"];
ode140 = x^2*(D[y[x], x] + y[x]^2) == -4*x*y[x] - 2
DSolve[%, y[x], x] // TraditionalForm
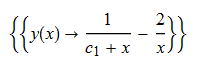
|
|
|
#141 \(x^{2}(y^{\prime }\left ( x\right ) +y\left ( x\right ) ^{2})+axy\left ( x\right ) =-b\)
Maple
restart;
ode141:=x^2*(y(x)^2+diff(y(x),x))+a*x*y(x)=-b:
dsolve(%,y(x));
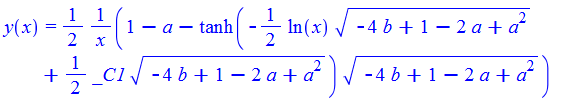
Mathematica
Clear["Global`*"];
ode141 = x^2*(D[y[x], x] + y[x]^2) + a*x*y[x] == -b
DSolve[%, y[x], x] // TraditionalForm
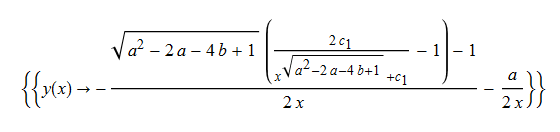
|
|
|
#142 \(x^{2}(y^{\prime }\left ( x\right ) -y\left ( x\right ) ^{2})-ax^{2}y\left ( x\right ) =-ax-2\)
Maple
restart;
ode142:=x^2*(-y(x)^2+diff(y(x),x))-a*x^2*y(x)=-2-a*x:
dsolve(%,y(x));
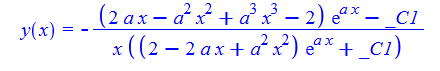
Mathematica
Clear["Global`*"];
ode142 = x^2*(D[y[x], x] - y[x]^2) - a*x^2*y[x] == -a*x - 2
DSolve[%, y[x], x] // TraditionalForm
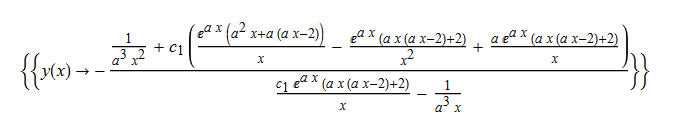
|
|
|
#143 \(x^{2}\left ( ay\left ( x\right ) ^{2}+y^{\prime }\left ( x\right ) \right ) =b\)
Maple
restart;
ode143:=x^2*(a*y(x)^2+diff(y(x),x))=b:
dsolve(%,y(x));
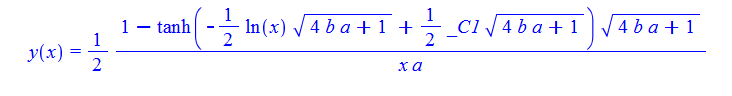
Mathematica
Clear["Global`*"];
ode143 = x^2*(D[y[x], x] + a*y[x]^2) == b
DSolve[%, y[x], x] // TraditionalForm
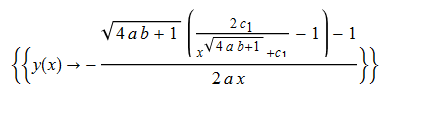
|
|
|
#144 \(x^{2}\left ( ay\left ( x\right ) ^{2}+y^{\prime }\left ( x\right ) \right ) +c+bx^{\alpha }=0\)
Maple 17
restart;
ode144:=x^2*(a*y(x)^2+diff(y(x),x))+b*x^alpha+c=0:
dsolve(%,y(x));
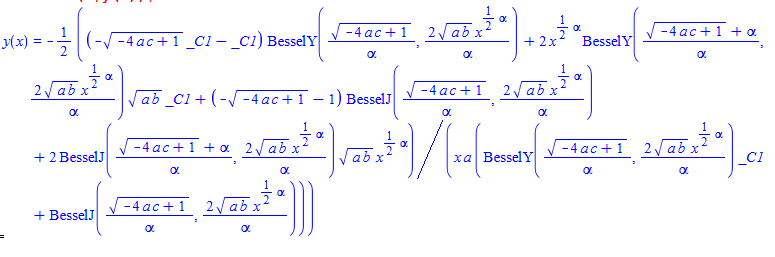
Mathematica 9.01
Clear["Global`*"];
ode144 = x^2*(D[y[x], x] + a*y[x]^2) + b*x^\[Alpha] + c == 0
DSolve[%, y[x], x]
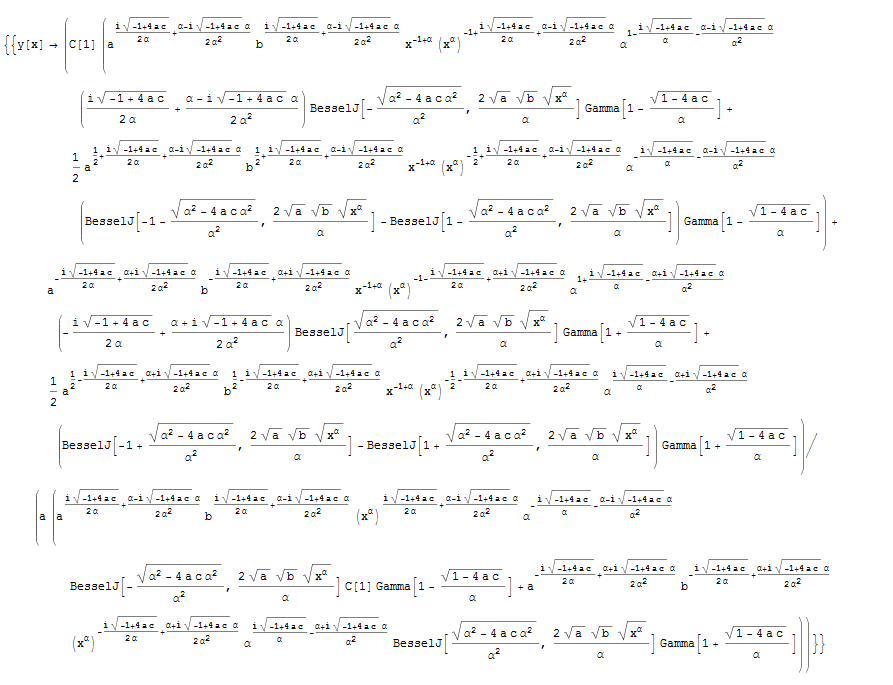
|
|
|
#145 \(-ax^{2}y^{2}\left ( x\right ) +ay^{3}\left ( x\right ) +x^{2}y^{\prime }\left ( x\right ) =0\)
Maple 17
restart;
ode145:=-a*x^2*y(x)^2+a*y(x)^3+x^2*diff(y(x),x)=0:
dsolve(%,y(x));
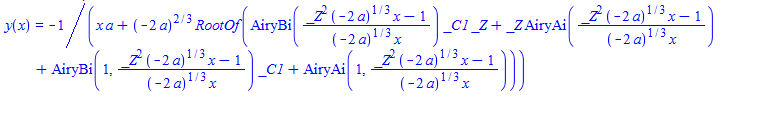
Mathematica 9.01
Clear["Global`*"];
ode145 = x^2*D[y[x], x] + a*y[x]^3 - a*x^2*y[x]^2 == 0
DSolve[%, y[x], x]
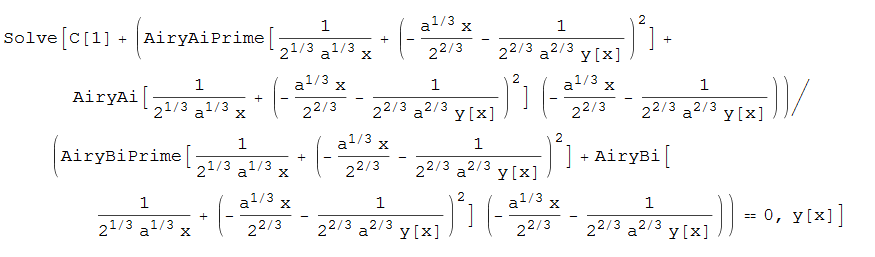
|
|
|
#146 \(x^2 y'(x)+a y(x)^2+x y(x)^3=0\)
Maple 17.01
restart;
ode146:=x^2*diff(y(x),x)+a*y(x)^2+x*y(x)^3=0:
dsolve(%,y(x));
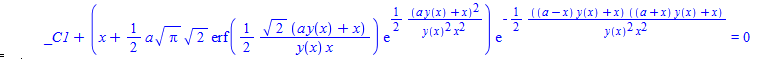
Mathematica 9.01
Clear["Global`*"];
ode146 = x^2*D[y[x], x] + x*y[x]^3 + a*y[x]^2 == 0
DSolve[%, y[x], x]
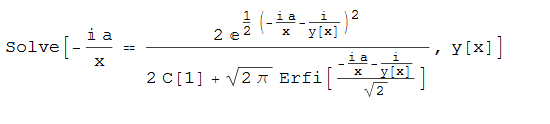
|
|
|
#147 \(a x^2 y(x)^3+b y(x)^2+x^2 y'(x)=0\)
Maple 17.01
restart;
ode147:=a*x^2*y(x)^3+b*y(x)^2+x^2 * diff(y(x),x)=0:
dsolve(%,y(x));
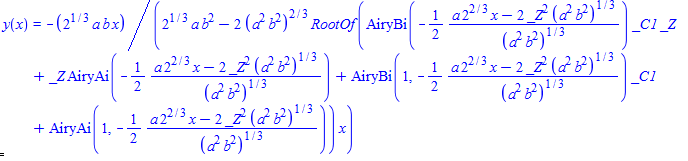
Mathematica 9.01
Clear["Global`*"];
ode147 = x^2*D[y[x], x] + a*x^2*y[x]^3 + b*y[x]^2 == 0;
DSolve[%, y[x], x]
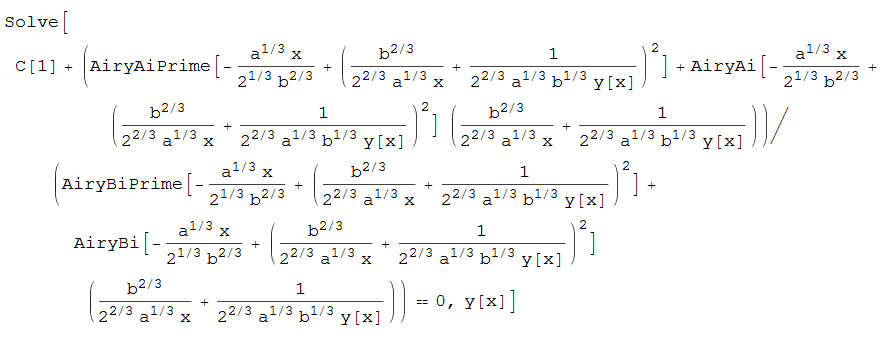
|
|
|
#148 \(\left (x^2+1\right ) y'(x)+x y(x)-1=0\)
Maple 17.01
restart;
ode148:=(x^2+1)* diff(y(x),x)+x*y(x)-1=0:
dsolve(%,y(x));
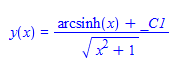
Mathematica 9.01
Clear["Global`*"];
ode148 = (x^2 + 1)*D[y[x], x] + x*y[x] - 1 == 0;
DSolve[%, y[x], x]
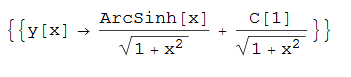
|
|
|
#149 \(\left (x^2+1\right ) y'(x)-x \left (x^2+1\right )+x y(x)=0\)
Maple 17.01
restart;
ode149:=(x^2+1)* diff(y(x),x)-x *(x^2+1)+x *y(x)=0:
dsolve(%,y(x));
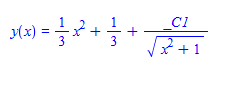
Mathematica 9.01
Clear["Global`*"];
ode149 = (x^2 + 1)*D[y[x], x] + x*y[x] - x*(x^2 + 1) == 0;
DSolve[%, y[x], x]
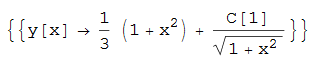
|
|
|
#150 \(\left (x^2+1\right ) y'(x)-2 x^2+2 x y(x)=0\)
Maple 17.01
restart;
ode150:=(x^2+1)* diff(y(x),x)-2* x^2+2* x* y(x)=0:
dsolve(%,y(x));
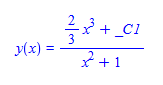
Mathematica 9.01
Clear["Global`*"];
ode150 = (x^2 + 1)*D[y[x], x] + 2*x*y[x] - 2*x^2 == 0;
DSolve[%, y[x], x]
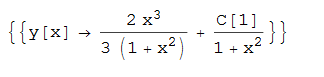
|
|
|
#151 \(\left (x^2+1\right ) y'(x)+(2 x y(x)-1) \left (y(x)^2+1\right )=0\)
Maple 17.01
restart;
ode151:=(x^2+1)* diff(y(x),x)+(2* x *y(x)-1)* (y(x)^2+1)=0:
dsolve(%,y(x));
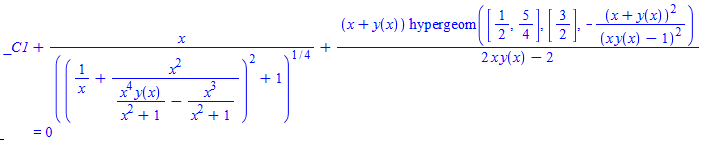
Mathematica 9.01
Clear["Global`*"];
ode151 = (x^2 + 1)*D[y[x], x] + (y[x]^2 + 1)*(2*x*y[x] - 1) == 0;
DSolve[%, y[x], x]
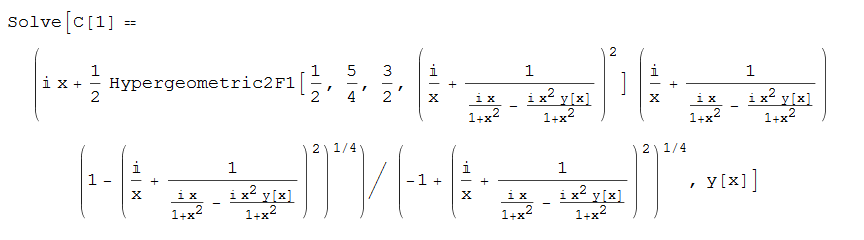
|
|
|
#152 \(\left (x^2+1\right ) y'(x)-x \left (x^2+1\right ) \cos ^2(y(x))+x \sin (y(x)) \cos (y(x))=0\)
Maple 17.01
restart;
ode152:=(x^2+1)*diff(y(x),x)-x * (x^2+1)* cos(y(x))^2+x* sin(y(x)) *cos(y(x))=0:
dsolve(%,y(x));
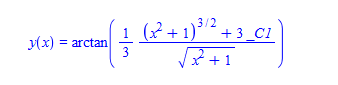
Mathematica 9.01
Clear["Global`*"];
ode152 = (x^2 + 1)*D[y[x], x] + x*Sin[y[x]]*Cos[y[x]] -
x*(x^2 + 1)*Cos[y[x]]^2 == 0;
DSolve[%, y[x], x]
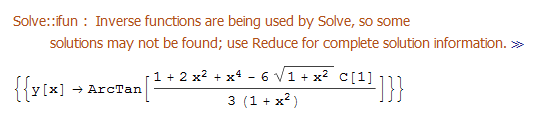
|
|
|
#153 \(a+\left (x^2-1\right ) y'(x)-x y(x)=0\)
Maple 17.01
restart;
ode153:=a+(x^2-1)* diff(y(x),x)-x* y(x)=0:
dsolve(%,y(x));
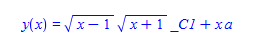
Mathematica 9.01
Clear["Global`*"];
ode153 = (x^2 - 1)*D[y[x], x] - x*y[x] + a == 0;
DSolve[%, y[x], x]
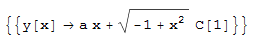
|
|
|
#154 \(\left (x^2-1\right ) y'(x)+2 x y(x)-\cos (x)=0\)
Maple 17.01
restart;
ode154:=(x^2-1)* diff(y(x),x)+2* x *y(x)-cos(x)=0:
dsolve(%,y(x));
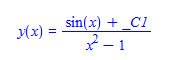
Mathematica 9.01
Clear["Global`*"];
ode154 = (x^2 - 1)*D[y[x], x] + 2*x*y[x] - Cos[x] == 0;
DSolve[%, y[x], x]
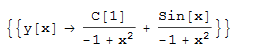
|
|
|
#155 \(\left (x^2-1\right ) y'(x)+y(x)^2-2 x y(x)+1=0\)
Maple 17.01
restart;
ode155:=(x^2-1)*diff(y(x),x)+y(x)^2-2* x* y(x)+1=0:
dsolve(%,y(x));
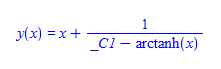
Mathematica 9.01
Clear["Global`*"];
ode155 = (x^2 - 1)*D[y[x], x] + y[x]^2 - 2*x*y[x] + 1 == 0;
DSolve[%, y[x], x]
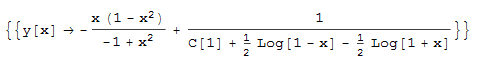
|
|
|
|
|
|