Pole assignment state feedback design example using Mathematica
Nasser M. Abbasi
Nov 29, 2014
Detailed step by step showing how to design a gain vector K for single input system in state space such that the system has desired pole locations.
Define the A and B matrices for state space x’=Ax+Bu
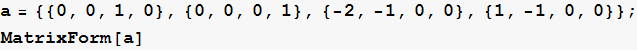

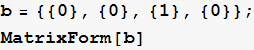
![]()
convert to controllable form (we call this the target system)


![]()
![]()
Obtain controllability matrix for original system


Obtain controllability matrix for target system


Obtain T, the transformation matrix
![]()

Verify T
![]()

define the gains as unknowns. These are what we will determine using pole assignment
![]()
generate the closed loop state feedback A matrix using the traget A,B system
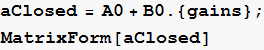
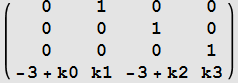
Find the CharacteristicPolynomial of the above matrix
![]()
![]()
Extract the coefficients so we can compare them to the design polynomial below
![]()
![]()
Generate the design polynomial from the desired pole locations
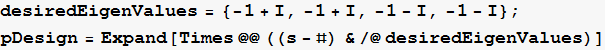
![]()
Extract the coefficients of the design polynomial
![]()
![]()
Solve for the gains by comparing coefficients of design polynomial with the closed loop polynomial

![]()
Convert the gain vector to original space using the transformation T found above
![]()
![]()
verify the original space now has designed eigenvalues with this gain vector
![]()
![]()
Using packaged function for design
The above design is implemented in my package now using the function nma`getStateGainVector. Here are examples using it
![]()

![]()
Another example

![]()
Turn on the flag to see the steps made in the design
![]()






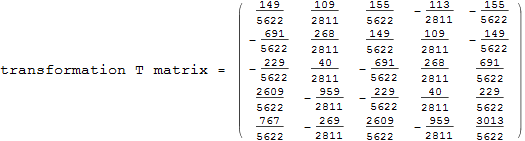
![]()
![]()
![]()
![]()