2.40 evaluate and plot a f(x,y) on 2D grid of coordinates

Evaluate \(x \exp ^{-x^2-y^2}\) on 2D cartesian grid between \(x=-2 \cdots 2\) and \(y=-4 \cdots 4\) using \(h=0.2\) for grid spacing.

Mathematica

f[x_,y_]:=x Exp[-x^2-y^2]; 
data = Table[f[x,y],{x,-2,2,.2},{y,-4,4,.2}]; 
ListPlot3D[data, 
 PlotRange->All, 
 ColorFunction->"Rainbow", 
 AxesLabel->{"x","y","z"}, 
 LabelStyle->12, 
 Ticks->{Range[-2,2,1],Range[-4,4,1],Automatic}, 
 DataRange->{{-2,2},{-4,4},Automatic}, 
 ImageSize->400]
 

The above can also be done using Plot3D

f[x_,y_]:=x Exp[-x^2-y^2]; 
Plot3D[f[x,y],{x,-2,2},{y,-4,4}, 
 PlotRange->All, 
 ColorFunction->"Rainbow", 
 AxesLabel->{"x","y","z"}, 
 LabelStyle->12, 
 ImageSize->400]
 

I need to sort out the orientation difference between the two plots above.

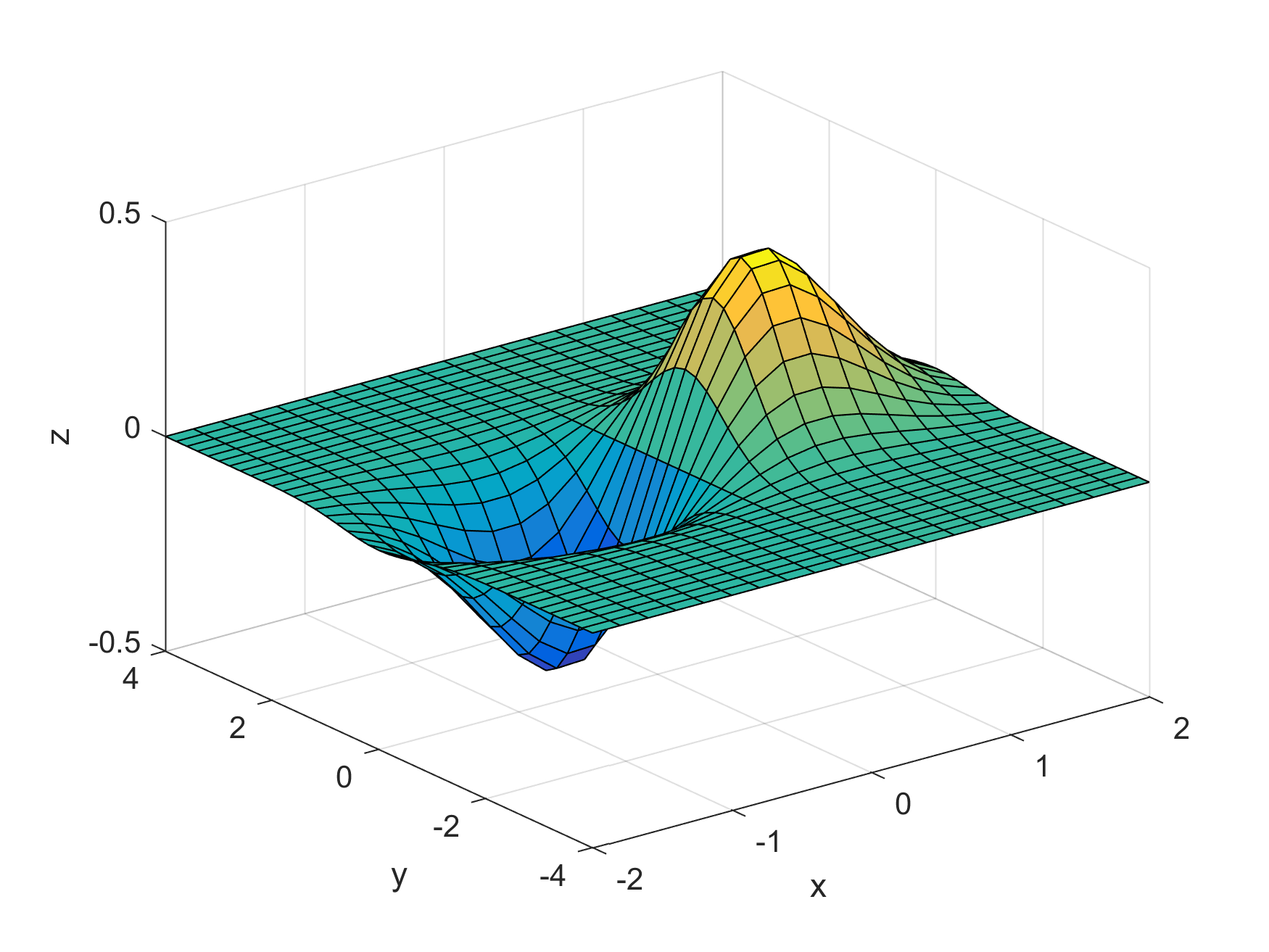
Matlab

[X,Y] = meshgrid(-2:.2:2, -4:.2:4); 
 Z = X .* exp(-X.^2 - Y.^2); 
 surf(X,Y,Z) 
 xlabel('x'); 
 ylabel('y'); 
 zlabel('z');
 

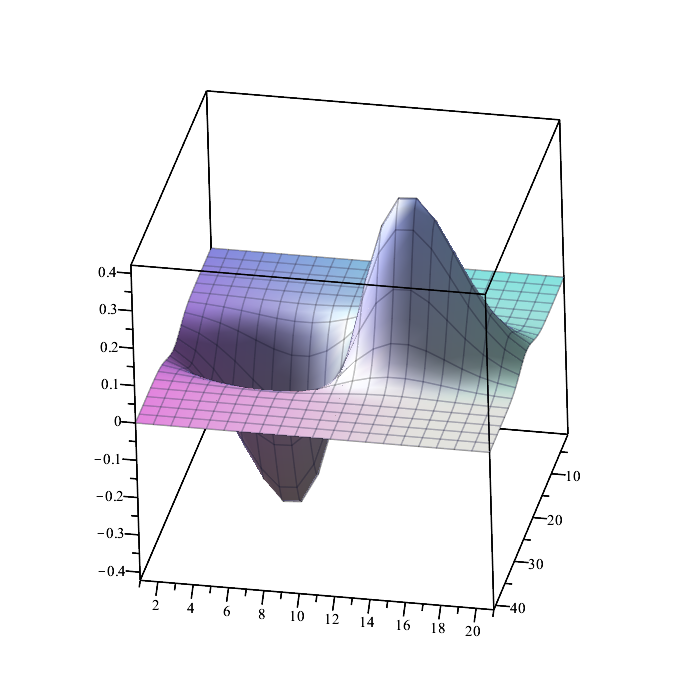
Maple

f:=(x,y)->x*exp(-x^2-y^2); 
data:=[seq([seq(f(x,y),x=-2..2,.2)],y=-4..4,.2)]: 
plots:-listplot3d(data)