Project, EGME 511 (Advanced Mechanical Vibration) Analysis of Van Der Pol diﬀerential equation

Project, EGME 511 (Advanced Mechanical Vibration)
Analysis of Van Der Pol diﬀerential equation

Nasser M. Abbasi

June 28, 2015

1 Introduction
2 Stability
3 Phase diagram
4 Phase diagram

This report in PDF

1 Introduction

Van der Pol diﬀerential equation is given by

( ) x′′(t) − c 1 − x2 x′(t) + kx (t) = 0

In this analysis, we will consider the case only for positive $c,k$ . We will analyze the stability of this equation and generate a phase diagram.

2 Stability

The ﬁrst step in examining stability of a non-linear diﬀerential equation is to convert it to state space by introducing 2 state variables.

} } } x1 = x x′1 = x′ x ′1 = x2 ′ → ′ ′′ 2 ′ → ′ 2 x2 = x x2 = x = c (1 − x )x − kx x 2 = c(1 − x1)x2 − kx1

Therefore

( ) ( ) ( ) x′1 x2 g(x1,x2) ′ = 2 = x2 c(1 − x1) x2 − kx1 f (x1,x2)

Equilibrium points are found by solving $( ) ( ) x′1 0 x′ = 0 2$ , hence from the above, we see that $x2 = 0$ and from $2 c (1 − x 1)x2 − kx1 = 0$ we conclude that $x1 = 0$ as well. Hence

( ) 0 xeq = 0

The system matrix is now found. First we note that $-∂g ∂g- ∂f- ∂x1 = 0, ∂x2 = 1, ∂x1 = − 2cx2x1 − k$ , and $∂∂xf = − cx21 + c 2$ , hence

( ) ( ) ∂∂gx- ∂∂gx- 0 1 A = ∂f1 ∂f2 = 2 ∂x1 ∂x2 − 2cx2x1 − k − cx 1 + c

Hence $A$ at $xeq$ becomes

( ) 0 1 A = − k c

Now we ﬁnd the characteristic equation

Hence $√ -------- √ -------- λ1,2 = −b2 ± 12 b2 − 4ac = c ± 12 c2 − 4k$ , therefore

√ ------ λ1,2 = c ± 1- c2 − k 2

If $2 c > k$ then both roots are on the RHS, hence system is unstable (equilibrium point is a repelling point).

If $c2 < k$ then we have $λ1,2 = c ± jβ$ , and we have spiral out equilibrium point, unstable.

3 Phase diagram

We need to obtain a relation between $x2$ and $x1$ . From the diﬀerential equation

( ) x′′(t) − c 1 − x2 x′(t) + kx (t) = 0

rewrite in state space variables, we obtain

Hence the above is in the form $dx2= f (x ,x ) dx1 1 2$ , therefore the isoclines lines can be found by setting

f (x1, x2) = ξ

Where $ξ$ is a constant. Hence we obtain the parameterize equation to use to plot the gradient lines as

c-(1 −-x21)x2-−-kx1 ξ = x2

4 Phase diagram

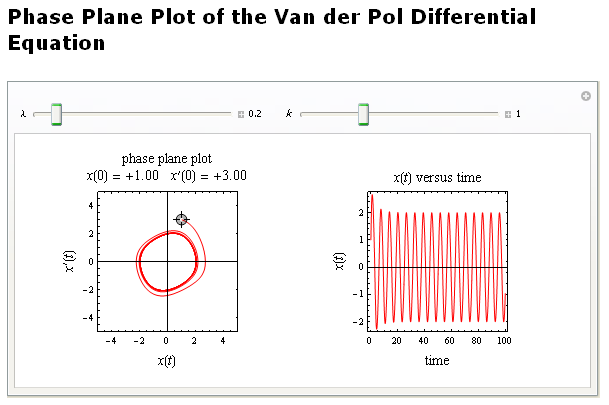
To generate the phase diagram¹ , a program was written which allows one to adjust the initial conditions and the parameters $k$ and $c$ and observe the eﬀect on the shape of the limit cycle. We see that starting from diﬀerent initial conditions, the solution trajectory always ends up in a limit cycle.

The following is a screen shot of the program written for this project.