Model of the spinning top gyro used in simulation

1.: up
2.: This page in PDF

Model of the spinning top gyro used in simulation

Nasser M. Abbasi

June 28, 2015

Figure 1: Geometry of the spinning top

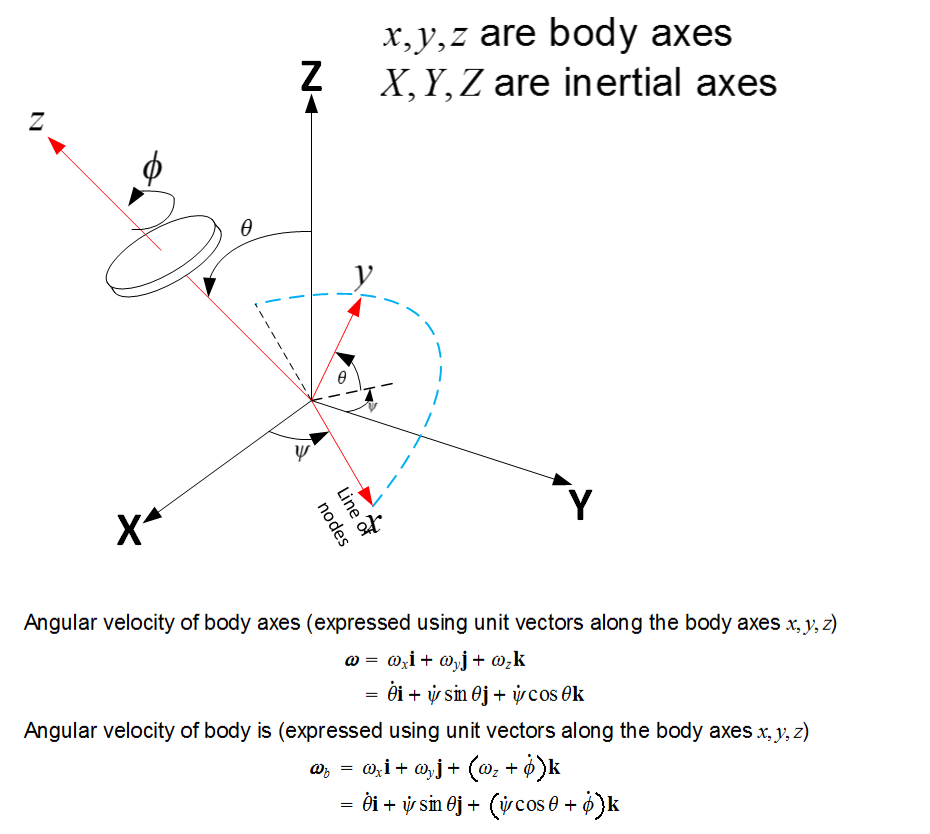
Let $x,y,z$ be the body axes. In this case, the body spins around one of its body axes (the z-axis). This is diﬀerent from other cases looked at before where the body axes and the body all move with same angular velocities.

Let $X, Y,Z$ be the inertial axes. Angular velocity of body axes (expressed using unit vectors along the body axes $x,y,z$ ) is

The angular velocity of the body (the spinning top) is

Euler equation of motion is

M = H˙ + ω × H

(1)

Where here $ω$ here always refer to the angular velocity of the body axes. The angular momentum of the body however, should add the additional spin of the body around its own body axes. This results in

(| Hx )| (| Ixωx )| H = | H | = | Iyωy | ( y) ( ( )) Hz Iz ωz + ˙ϕ

Notice the additional body spin speed added to the third component above.

And since $Ix = Iy = Io$ in this case, which is due to symmetry of the body itself, the above becomes

( ) ( ) Ioωx Io𝜃˙ || || || ˙ || H = ( (Ioωy )) = ( ( Ioψ sin 𝜃 ) ) Iz ωz + ˙ϕ Iz ψ˙cos𝜃 + ϕ˙

Taking derivative gives

( ) ( ) Ioω˙x ( Io𝜃¨ ) ˙ || || || ¨ ˙ ˙ || H = ( (Ioω˙y )) = ( I(o ψ sin 𝜃 + ψ𝜃 cos𝜃 ) ) Iz ω˙z + ϕ¨ I ¨ψ cos𝜃 − ψ˙˙𝜃sin𝜃 + ¨ϕ z

From (1), Euler equation of motion of the spinning top becomes

Simplifying results in

The above are the three equations that are solved for $𝜃 (t),ψ (t) ,ϕ(t)$ to obtain the equations used to simulate the spinning top. Numerical solver is used and the time step is adjusted in the simulation as needed. A complete demonstration is build showing the motion with many diﬀerent controls to allow diﬀerent analysis to be carried out on the spinning top motion.

The above equations can be put in state space formulation to allow one to use ode45 solver if needed as follows. Let $x1 = 𝜃 (t),x2 = ψ (t),x3 = ϕ(t),x4 = 𝜃′(t),x5 = ψ′(t),x6 = ϕ′(t)$ then

( ) ( ) x ′ x4 | 1| | | || x ′2|| || x5 || || x ′|| || x || | 3| = | 6 | || x ′4|| || 1Io (− mgL sin x1 − Izx5sinx1 (x5cos x1 + x6) + Iox25sin x1 cosx1) || || ′|| || ---1-- (I x (x cos x + x ) − I2x x cos x ) || ( x 5) ( ( I0sinx(1 z 4 5 1 6 o 5 4 1 ) )) x ′6 1I- x5x4 sinx1 − Iz I-1sinx-(Izx4 (x5cos x1 + x6 ) − Io2x5x4 cosx1 ) cos x1 z 0 1

If using ode45, then the RHS above is what the ode45 function needs to compute.