HOME
PDF version of document
Generating the four Kharitonov polynomials and displaying corresponding Hurwitz stability matrix
by Nasser M. Abbasi
Nov 27, 2014
Introduction
Software written in Mathematica to generate the four Kharitonov’s polynomials from the interval polynomial specification and construct the four Hurwitz stability matrices to test for stability of each polynomial. Examples from chapter 5, “New tools for robustness of linear systems” by Professor B. Ross Barmish are used for illustration.
Example 5.5.2
This function takes interval polynomal and generates the 4 Kharitonov’s polynomials
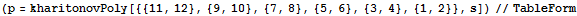
This function takes the result and generate the Hurwitz matrix and root locations. The polynomial is stable when all leading minors are positive.
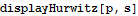
| Hurwitz Matrix |
 |
root locations |
Real part of roots |
|
|
|
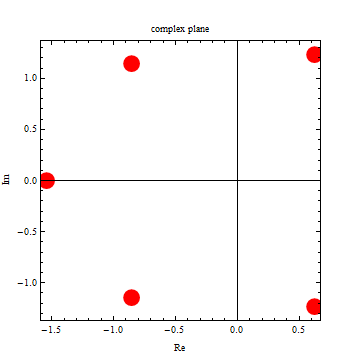
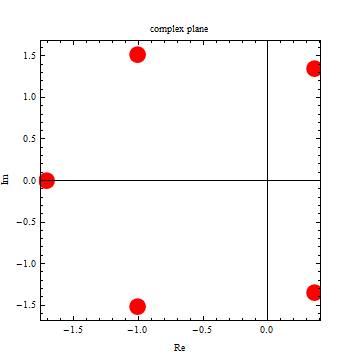 |
| -1.71185 |
| -1.00624 |
| -1.00624 |
| 0.362161 |
| 0.362161 |
|
|
|
|
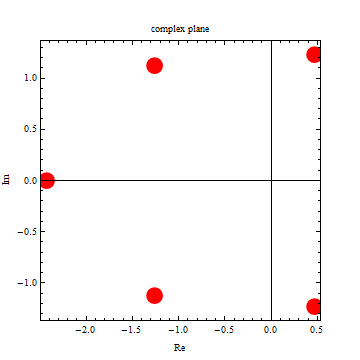
 |
| -1.5452 |
| -0.854858 |
| -0.854858 |
| 0.627459 |
| 0.627459 |
|
|
|
|
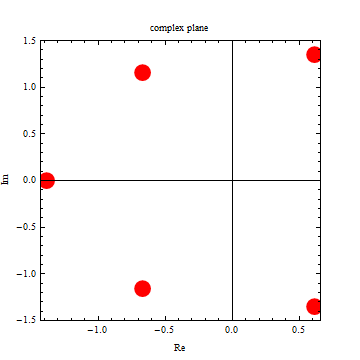
 |
| -2.43433 |
| -1.25737 |
| -1.25737 |
| 0.474539 |
| 0.474539 |
|
|
|
|
 |
| -1.3877 |
| -0.672514 |
| -0.672514 |
| 0.616365 |
| 0.616365 |
|
Example 5.6.2
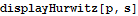
| Hurwitz Matrix |
 |
root locations |
Real part of roots |
|
|
|
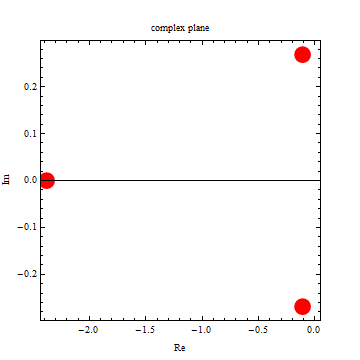 |
| -2.38347 |
| -0.108264 |
| -0.108264 |
|
|
|
|
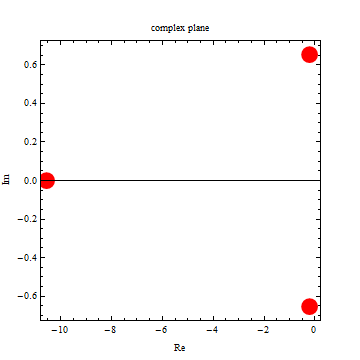 |
| -10.5718 |
| -0.21411 |
| -0.21411 |
|
|
|
|
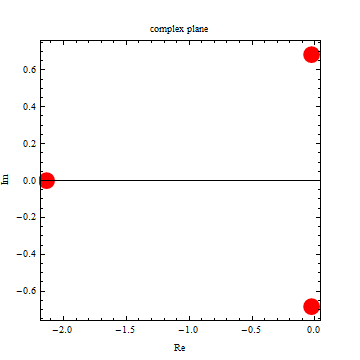 |
| -2.13812 |
| -0.0309384 |
| -0.0309384 |
|
|
|
|
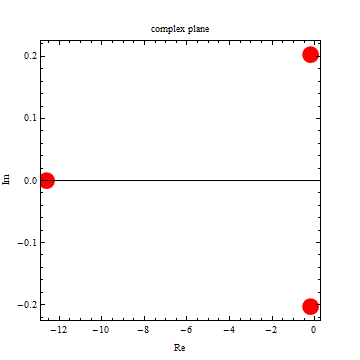 |
| -12.6098 |
| -0.195114 |
| -0.195114 |
|
Example 5.10.1
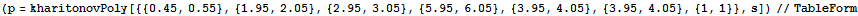
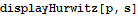
| Hurwitz Matrix |
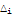 |
root locations |
Real part of roots |
|
|
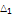 |
1.95 |
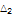 |
3.225 |
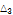 |
7.9575 |
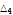 |
9.39937 |
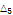 |
6.41034 |
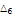 |
6.41034 |
|
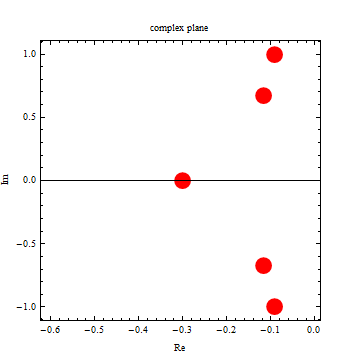 |
| -3.2334 |
| -0.299508 |
| -0.116271 |
| -0.116271 |
| -0.0922772 |
| -0.0922772 |
|
|
|
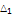 |
2.05 |
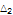 |
2.775 |
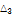 |
4.0575 |
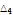 |
2.49938 |
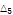 |
0.404656 |
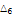 |
0.404656 |
|
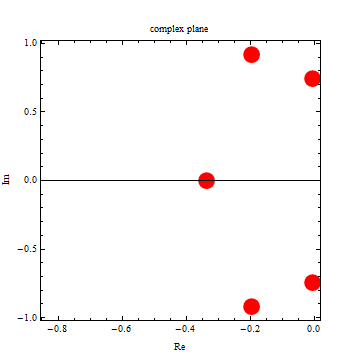 |
| -3.3032 |
| -0.338496 |
| -0.1981 |
| -0.1981 |
| -0.00605111 |
| -0.00605111 |
|
|
|
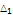 |
1.95 |
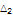 |
2.425 |
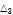 |
3.5075 |
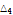 |
3.11438 |
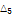 |
2.34509 |
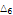 |
2.34509 |
|
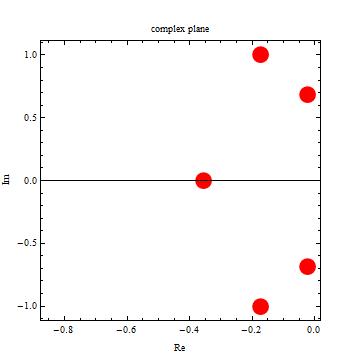 |
| -3.20234 |
| -0.356709 |
| -0.173359 |
| -0.173359 |
| -0.0221182 |
| -0.0221182 |
|
|
|
 |
2.05 |
 |
3.575 |
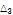 |
8.4075 |
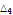 |
7.81438 |
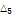 |
2.68991 |
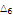 |
2.68991 |
|
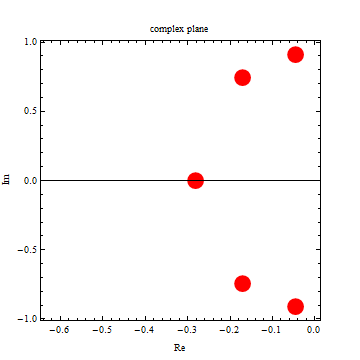 |
| -3.33369 |
| -0.281521 |
| -0.17061 |
| -0.17061 |
| -0.0467823 |
| -0.0467823 |
|
page 71 example, in conlcusion
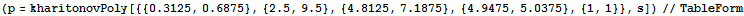
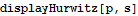
| Hurwitz Matrix |
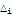 |
root locations |
Real part of roots |
|
|
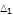 |
2.5 |
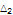 |
16.3945 |
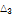 |
76.3375 |
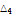 |
76.3375 |
|
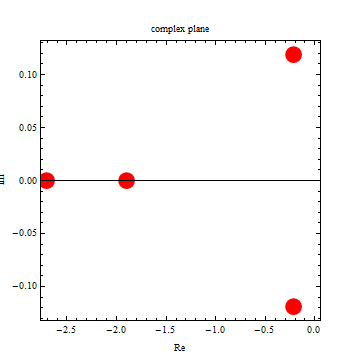 |
| -2.70998 |
| -1.89535 |
| -0.216088 |
| -0.216088 |
|
|
|
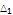 |
9.5 |
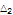 |
42.3173 |
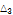 |
119.115 |
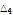 |
119.115 |
|
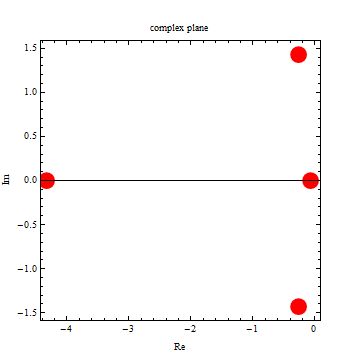 |
| -4.33442 |
| -0.269038 |
| -0.269038 |
| -0.0750017 |
|
|
|
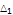 |
2.5 |
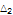 |
8.56797 |
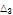 |
36.9111 |
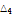 |
36.9111 |
|
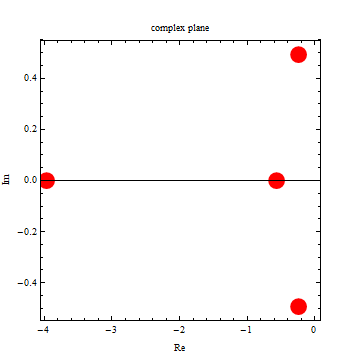 |
| -3.9738 |
| -0.568926 |
| -0.247385 |
| -0.247385 |
|
|
|
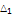 |
9.5 |
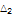 |
66.7352 |
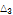 |
239.922 |
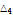 |
239.922 |
|
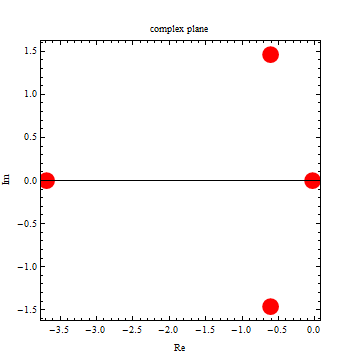 |
| -3.69136 |
| -0.611201 |
| -0.611201 |
| -0.033736 |
|
![]()
![]()




![]()
![]()




![]()
![]()




![]()
![]()



