|
# |
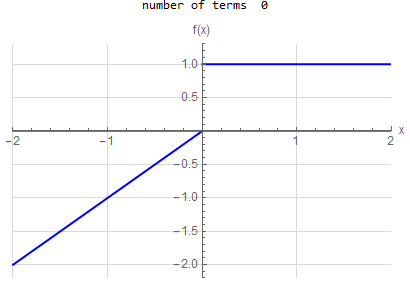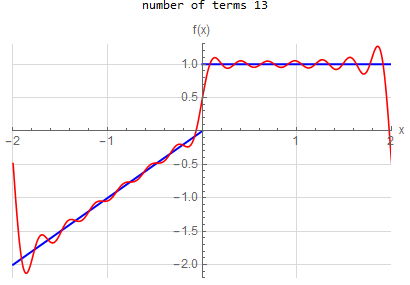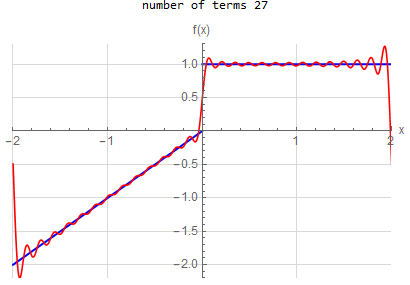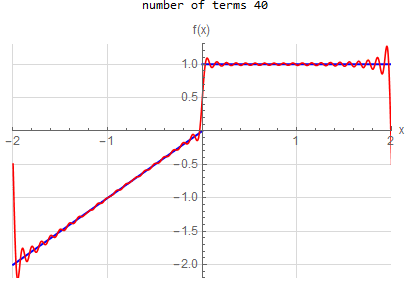
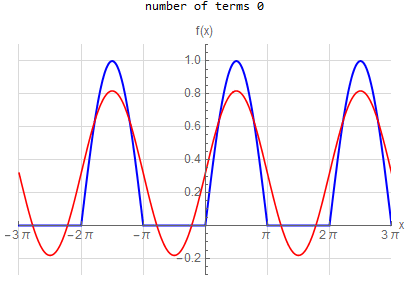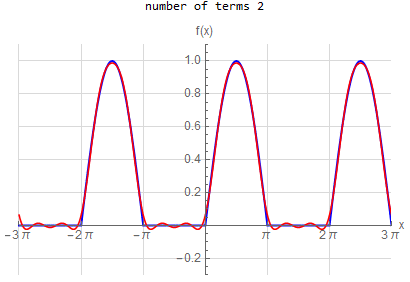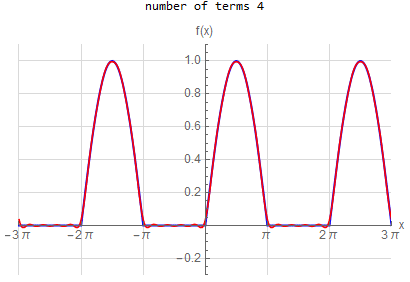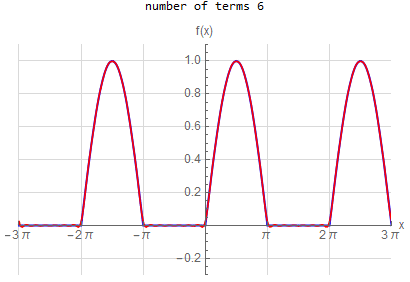
Fourier series over original domain |
Fourier series over periodic extended domain |
|
1 |
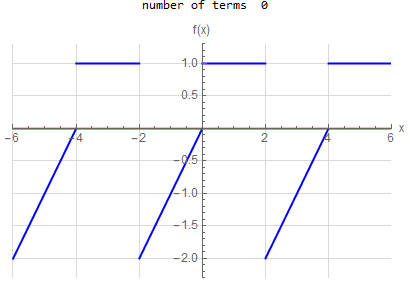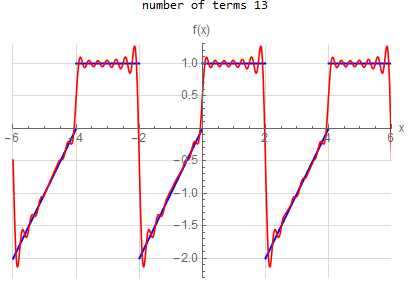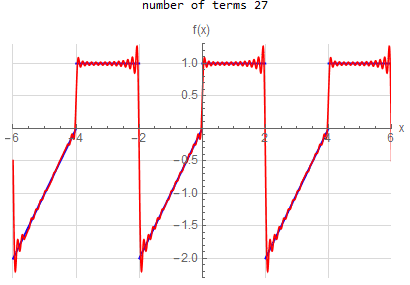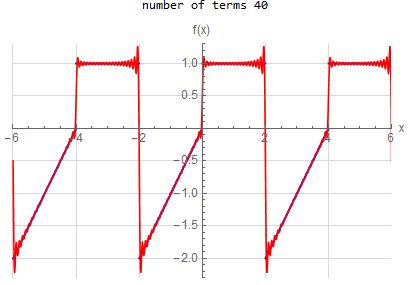
f\left (x\right ) =\begin{cases} x & -2<x<0 \\ 1 & 0<x<2 \end{cases} \hspace{15pt} -2<x<2 f\left ( x\right ) \sim 2 \sum _{n=1}^{\infty } - \frac{2(-1+(-1)^n)}{n^2 \pi ^2} \cos (\frac{\pi }{2} n x) + \frac{1-3 (-1)^n}{n \pi } \sin (\frac{\pi }{2} n x) |
|
|
|
|
|
|
2 |
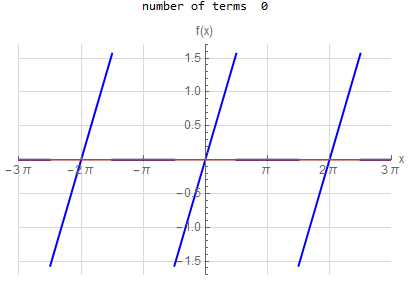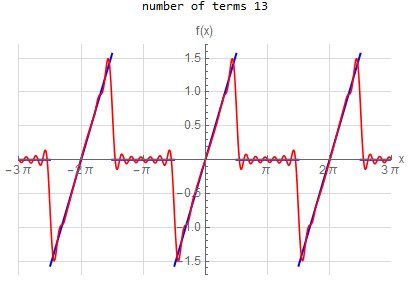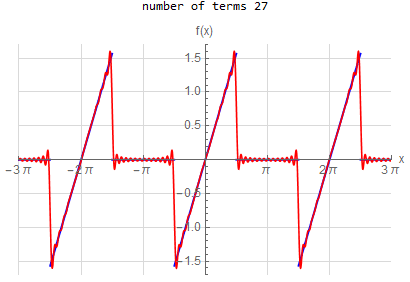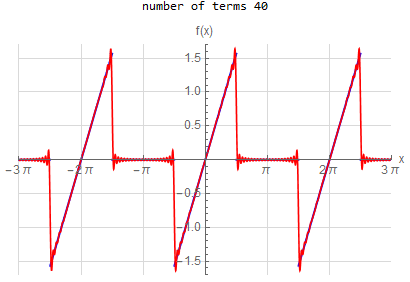
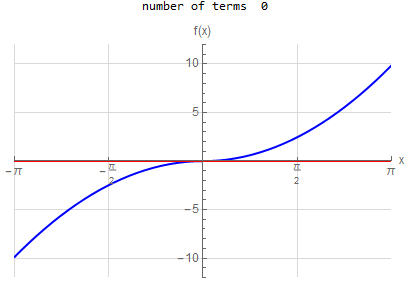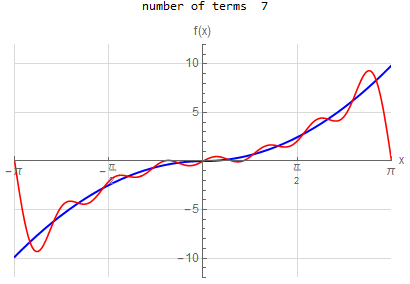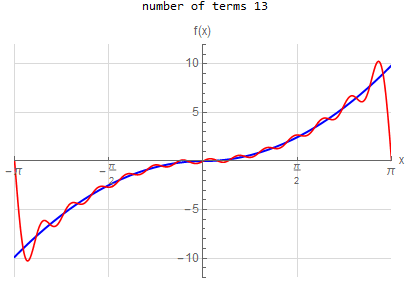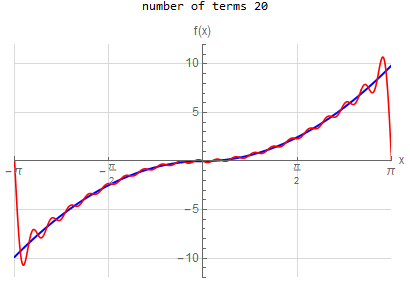
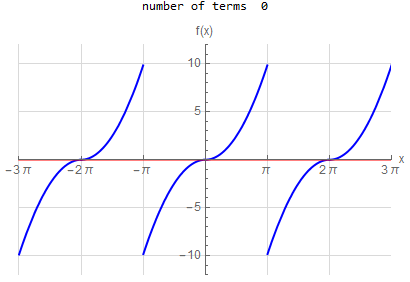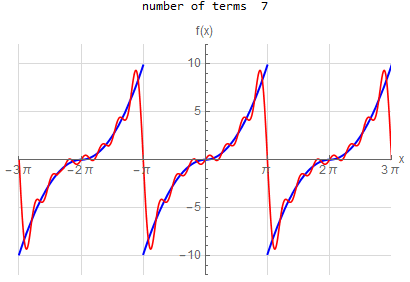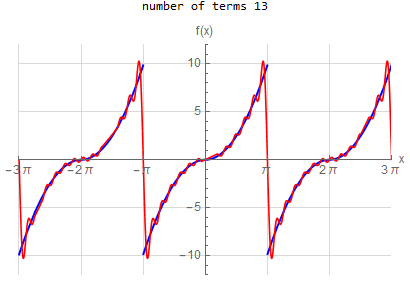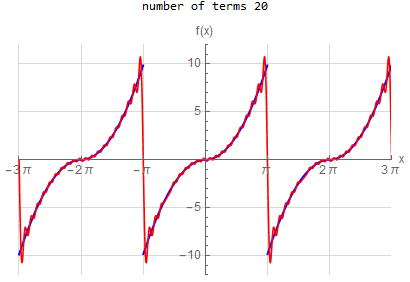
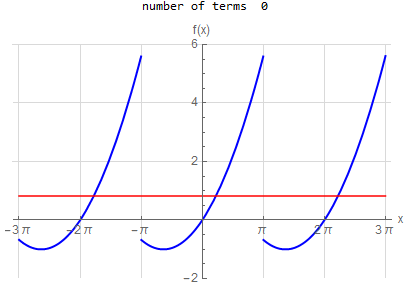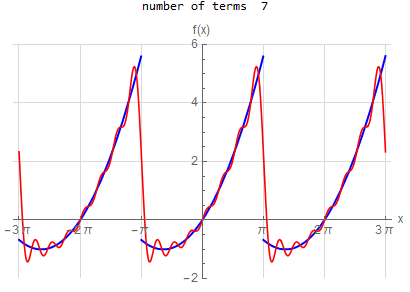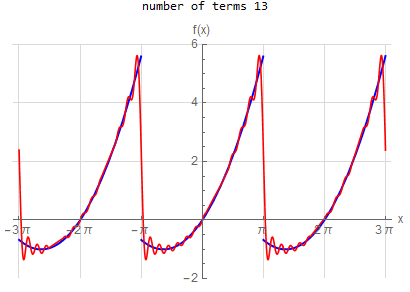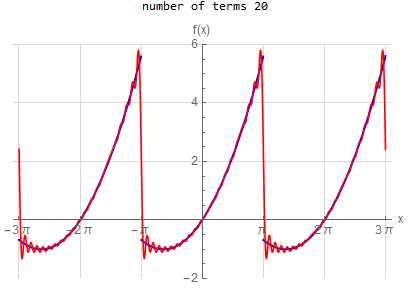
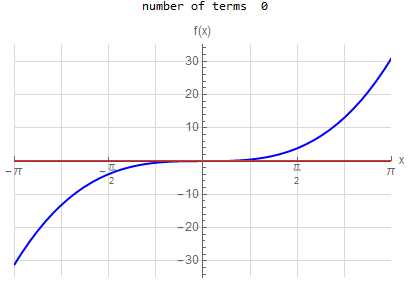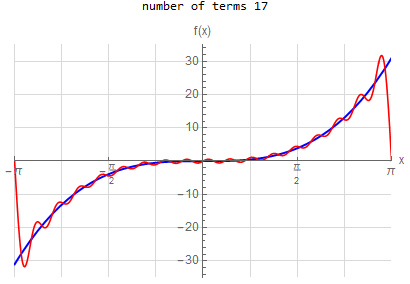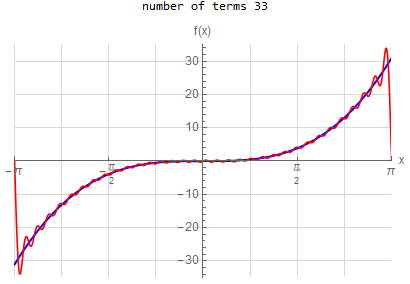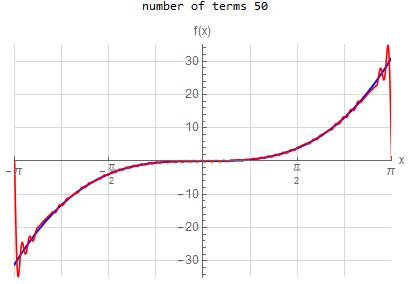
f\left (x\right ) =-x \hspace{15pt} -\pi <x<\pi f\left ( x\right ) \sim 2\sum _{n=1}^{\infty }\frac{\left ( -1\right ) ^{n}}{n}\sin \left ( nx\right ) |
|
|
|
|
|
|
3 |
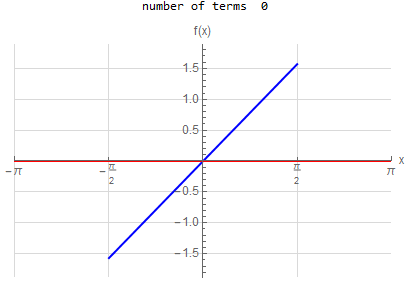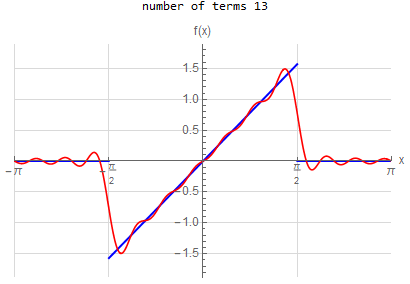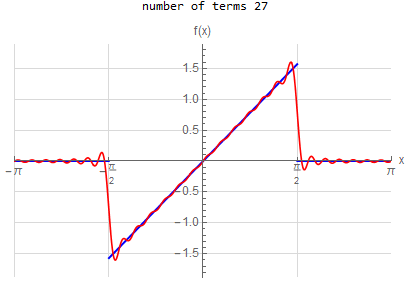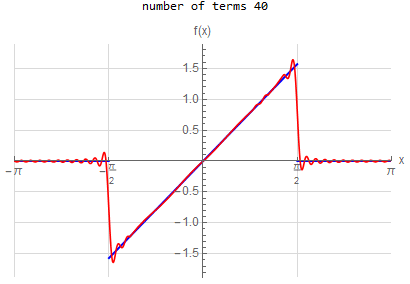
f\left ( x\right ) =\left \{ \begin{array} [c]{ccc}x & &\hspace{8pt} \left \vert x\right \vert <\frac{\pi }{2}\\ 0 & &\hspace{8pt} \text{ otherwise }\end{array} \right . \hspace{15pt} -\pi <x<\pi f\left ( x\right ) \sim \sum _{n=1}^{\infty }\frac{2}{\pi n^{2}}\left ( \sin \left ( \frac{n\pi }{2}\right ) -\frac{1}{2}n\pi \cos \left ( \frac{n\pi }{2}\right ) \right ) \sin \left ( nx\right ) |
|
|
|
|
|
|
4 |
f\left ( x\right ) =\left \{ \begin{array} [c]{ccc} -1 & &\hspace{8pt} -\pi \leq x\leq 0\\ 1 & &\hspace{8pt} 0<x\leq \pi \end{array} \right . \hspace{15pt} -\pi <x<\pi f(x) \sim \frac{4}{\pi } \sum _{n=1}^{\infty } \frac{1}{2 n- 1} \sin ( (2 n -1) x) |
|
|
|
|
|
|
5 |
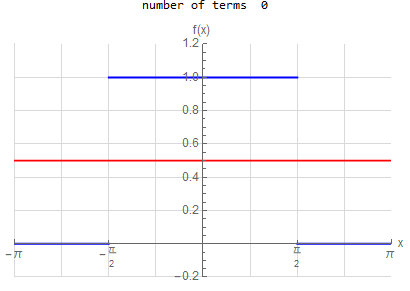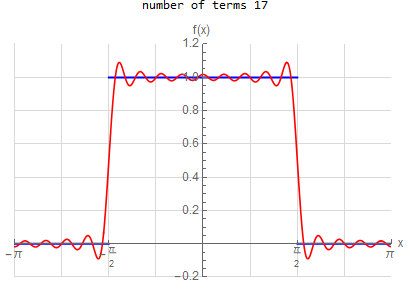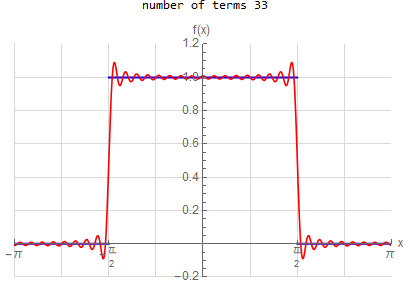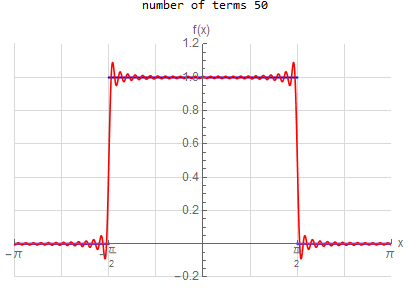
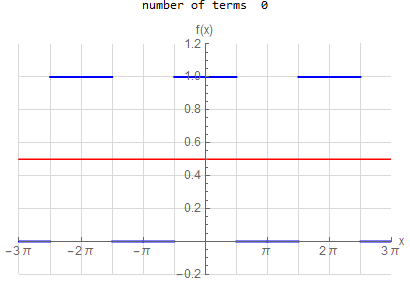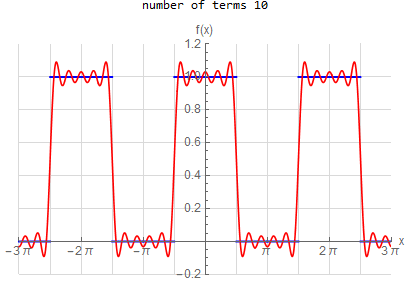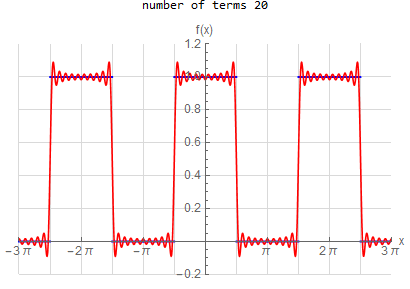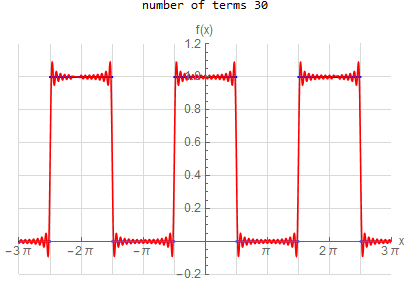
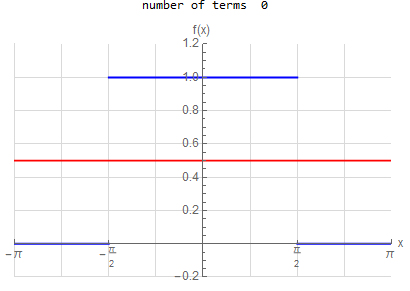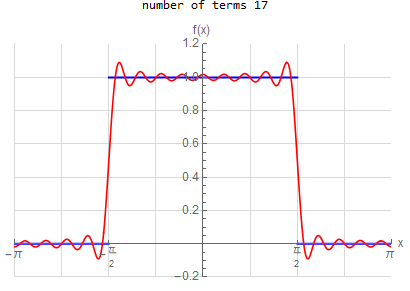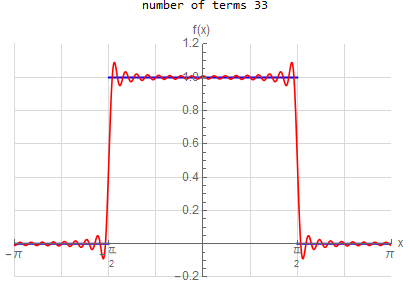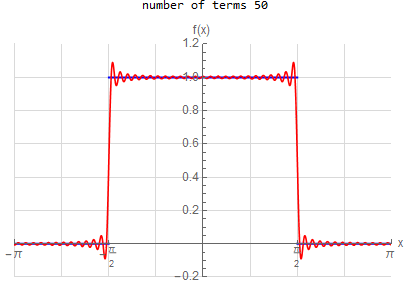
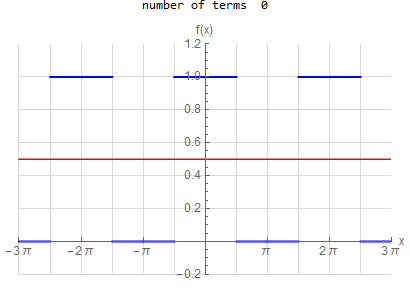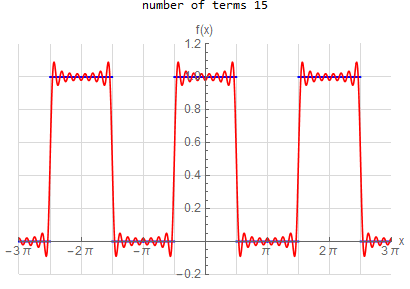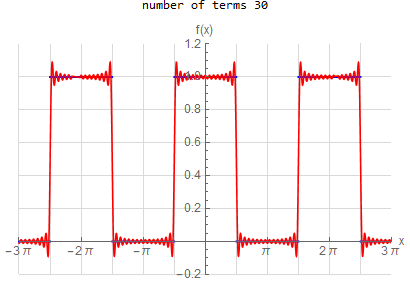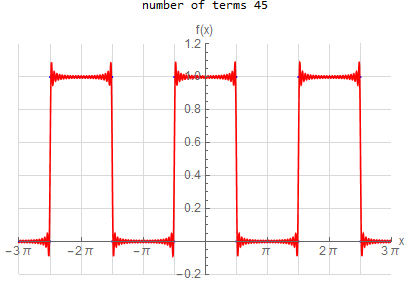
f\left ( x\right ) =\left \{ \begin{array} [c]{ccc} 1 & &\hspace{8pt} |x|< \frac{1}{2}\pi \\ 0 & &\hspace{8pt} \frac{1}{2}\pi <|x|< \pi \end{array} \right . \hspace{15pt} -\pi <x<\pi f(x) \sim \frac{1}{2} + \sum _{n=1}^{\infty } \frac{2}{\pi n} \sin ( \frac{n \pi }{2} ) \cos (n x) |
|
|
|
|
|
|
6 |
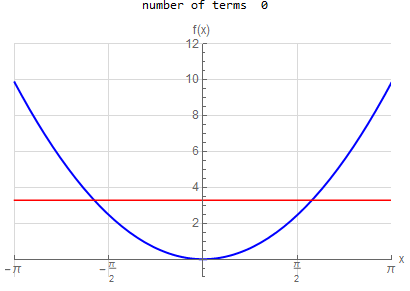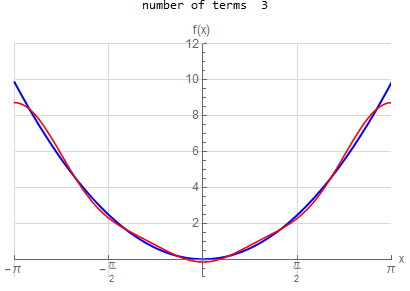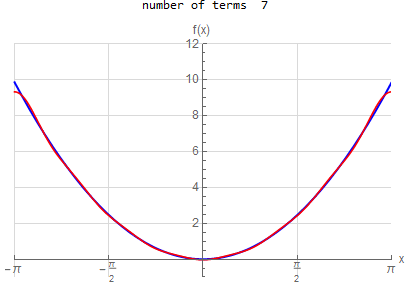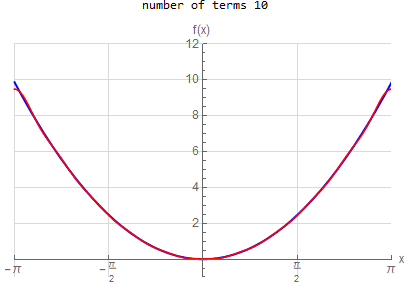
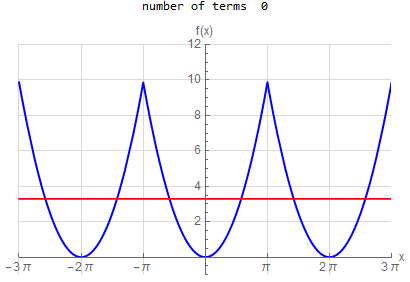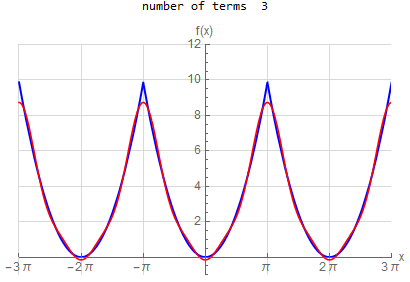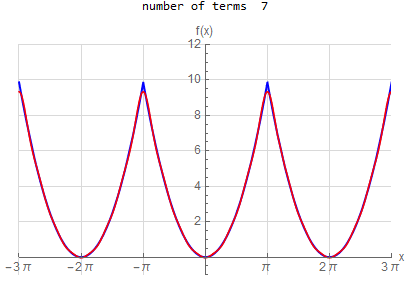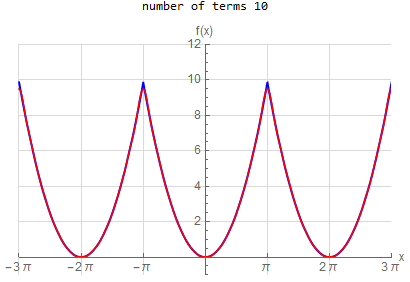
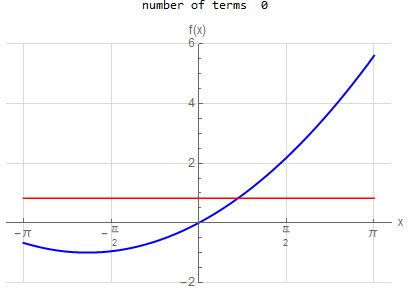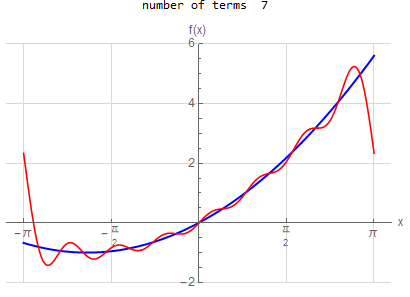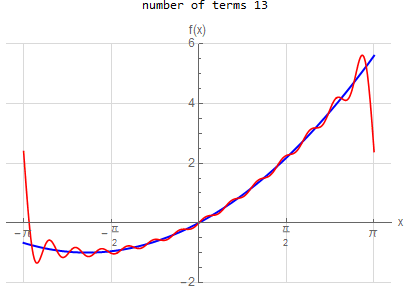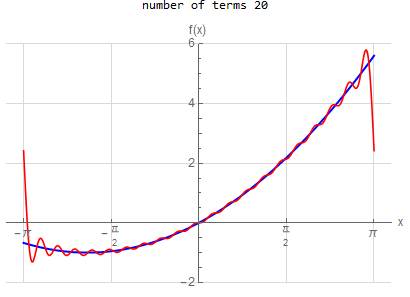
f\left ( x\right ) =x^{2} \hspace{15pt} -\pi <x<\pi f\left ( x\right ) \sim \frac{1}{3}\pi ^{2}+4\sum _{n=1}^{\infty }\frac{1}{n^{2}}\left ( -1\right ) ^{n}\cos \left ( nx\right ) |
|
|
|
|
|
|
7 |
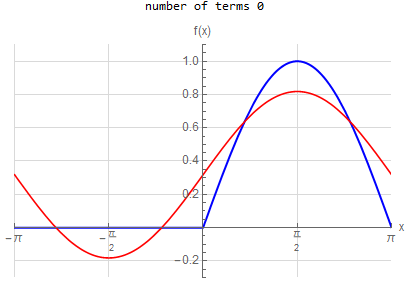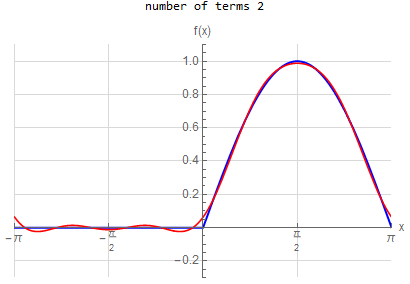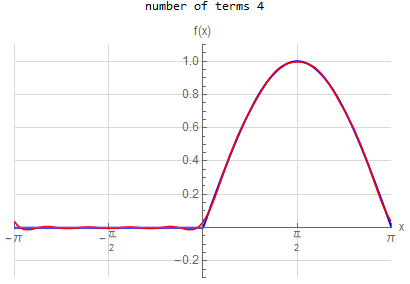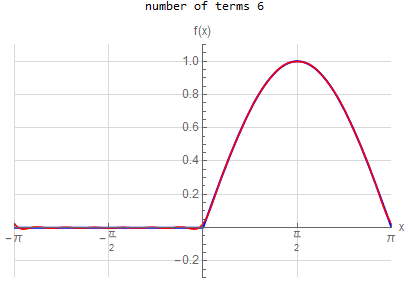
f\left ( x\right ) =\left \{ \begin{array} [c]{ccc}\sin x & & \hspace{8pt}0<x\leq \pi \\ 0 & & \hspace{8pt} -\pi \leq x<0 \end{array} \right . \hspace{15pt} -\pi <x<\pi f\left ( x\right ) \sim \frac{1}{\pi }+\frac{1}{2}\sin \left ( x\right ) +\frac{2}{\pi }\sum _{n=1}^{\infty }\frac{1}{1-\left ( 2n\right ) ^{2}}\cos \left ( 2nx\right ) |
|
|
|
|
|
|
8 |
f\left ( x\right ) =\left \{ \begin{array} [c]{ccc}x^{2} & & \hspace{8pt} 0<x\leq \pi \\ -x^{2} & & \hspace{8pt} -\pi \leq x<0 \end{array} \right . \hspace{15pt} -\pi <x<\pi f\left ( x\right ) \sim 2\pi ^{2}\sum _{n=1}^{\infty }\left ( \frac{1}{n\pi }\left ( -1\right ) ^{n+1}-\frac{2}{\left ( n\pi \right ) ^{3}}\left ( 1-\left ( -1\right ) ^{n}\right ) \right ) \sin \left ( nx\right )
|
|
|
|
|
|
|
9 |
f\left ( x\right ) =x+\frac{1}{4}x^{2} \hspace{15pt} -\pi <x<\pi f\left ( x\right ) \sim \frac{\pi ^{2}}{12}+\sum _{n=1}^{\infty }\left ( -1\right ) ^{n}\left ( \frac{\cos \left ( nx\right ) }{n^{2}}-\frac{2\sin \left ( nx\right ) }{n}\right )
|
|
|
|
|
|
|
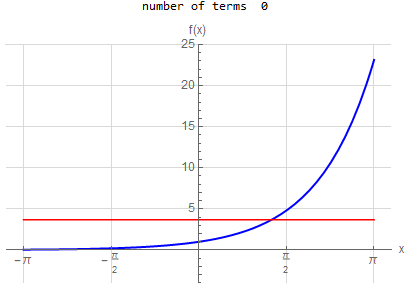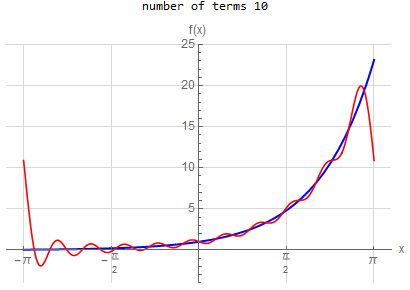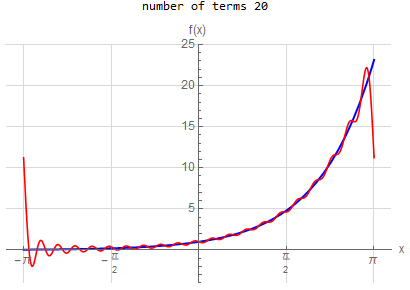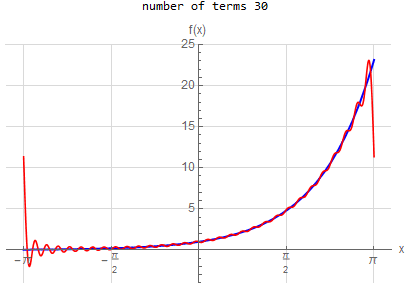
10 |
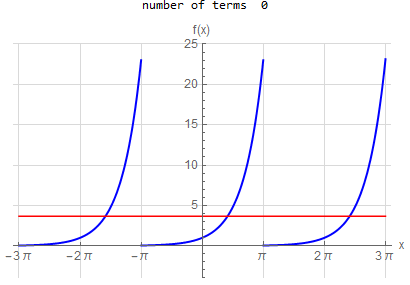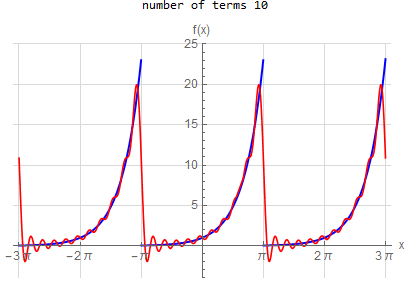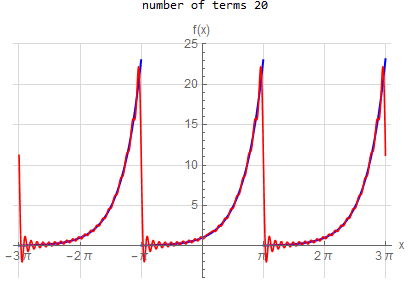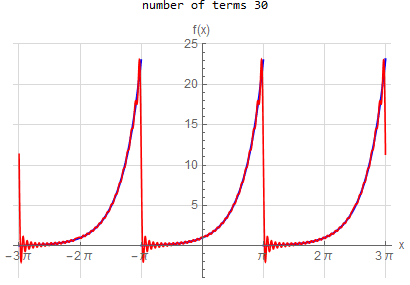
f\left ( x\right ) =e^{x} \hspace{15pt} -\pi <x<\pi f\left ( x\right ) \sim \frac{2\sinh \left ( \pi \right ) }{\pi }\left ( \frac{1}{2}+\sum _{n=1}^{\infty }\frac{\left ( -1\right ) ^{n}}{1+n^{2}}\left ( a\cos \left ( nx\right ) -n\sin \left ( nx\right ) \right ) \right )
|
|
|
|
|
|
|
11 |
f(x) =\begin{cases} 1 & \left | x\right | <\frac{\pi }{2} \\ 0 & \text{True} \end{cases} \hspace{15pt} -\pi <x<\pi f(x) \sim \frac{1}{2} + \sum _{n=1}^{\infty } \frac{2}{n \pi } \sin (\frac{n \pi }{2}) \cos (n x)
|
|
|
|
|
|
|
12 |
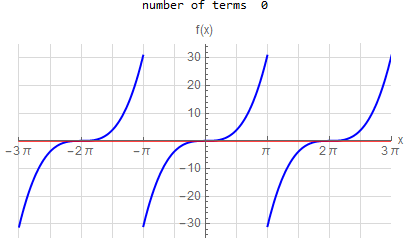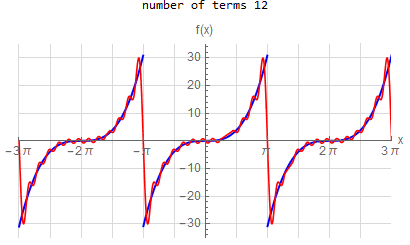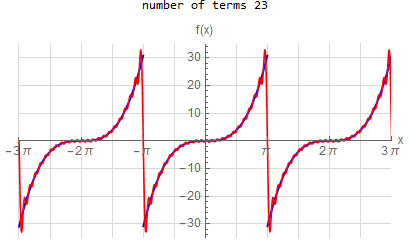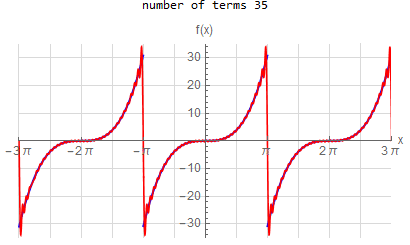
f(x) =x^3 \hspace{15pt} -\pi <x<\pi f(x) \sim \sum _{n=1}^{\infty } - \frac{ 2(-1)^n (-6 n^2 \pi ^2)}{n^3} \sin (n x)
|
|
|
|
|
|
|
13 |
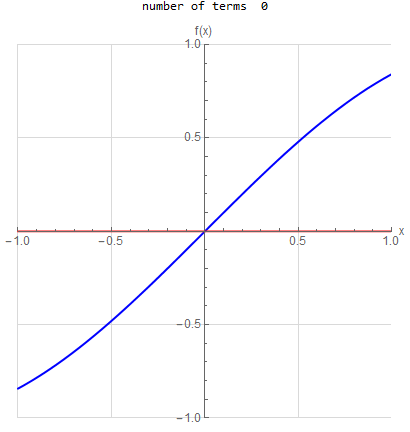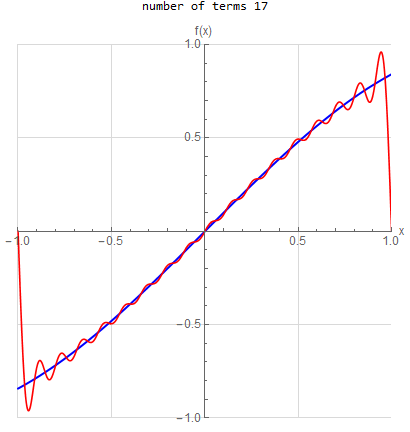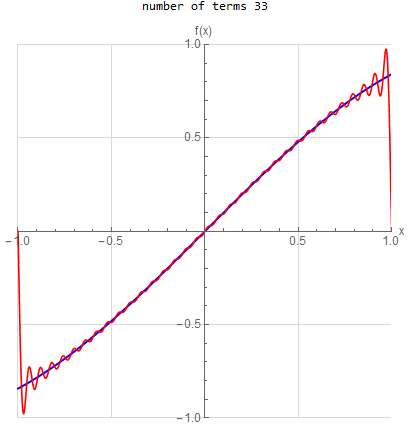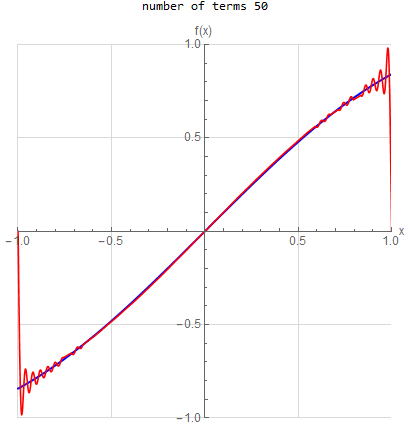
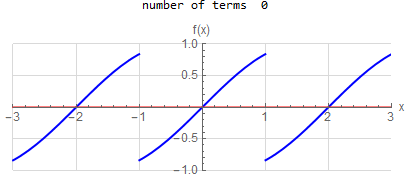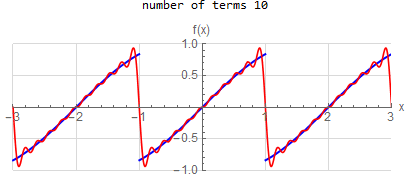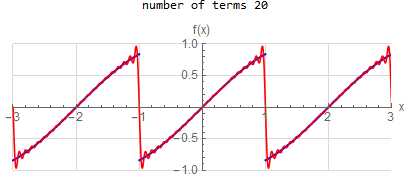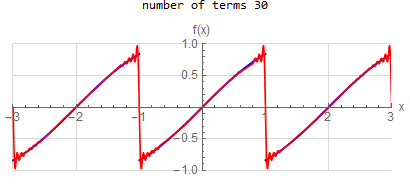
f(x) =\sin (x) \hspace{15pt} -1<x<1 f(x) \sim \sum _{n=1}^{\infty } - \frac{2 n \pi (-1)^n }{n^2 \pi ^2 -1} \sin (1) \sin (n \pi x)
|
|
|
|
|
|
|
|
||
|
|
||
|
|