Comparing the derivation of equation of motion for double pendulum by method of F=ma and by energy (Lagrangian) method
by Nasser M. Abbasi
May 11, 2011
The goal of this note is to show how to use a symbolic program to help solve a typical basic engineering problem that requires large amount of algebraic manipulation. By applying a CAS program such as Mathematica on such a problem, one can then concentrate more on the problem formulation itself by having the program do the long algebraic computation, which can be very time consuming if done by hand, and also can be error prone.
This also allows one to be able to experiment with different formulation, as one is now relieved from the time consuming part and is able to try different solutions and different idea, which can lead to better insight of the problem.
In this note, we solve the double pendulum problem both ways. One way is by using the energy method, and another way is by using F=ma approach. Both would require long time to do by hand due to the large amount of algebra involved. And at the end, both solutions are verified to be the same.
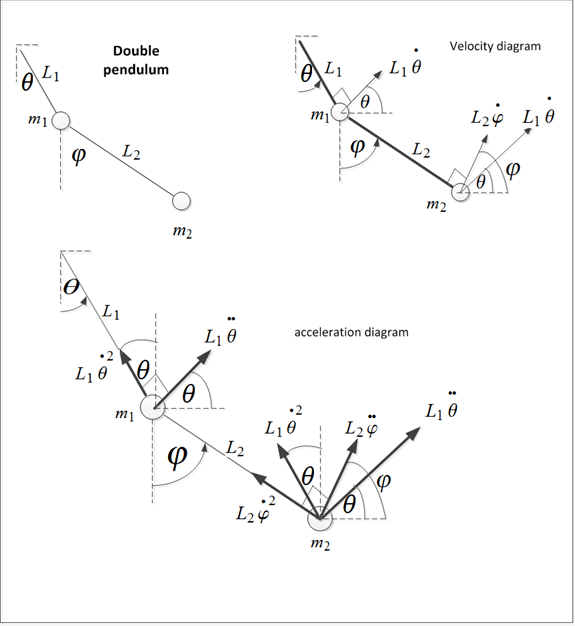
system diagram
This diagram shows the velocity and acceleration components of the 2 masses in the double pendulum.

Lagrangian solution
Write down the kinetic energy T
In[17]:=

Out[18]=
![]()
Write down the potential energy
In[19]:=
![]()
Out[20]=
![]()
Write down the Lagrangian L
In[21]:=
![]()
Out[22]=
![]()
Find equation of motion for θ
In[26]:=

Out[28]=
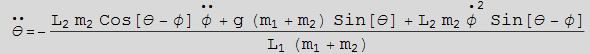
Find equation of motion for φ
In[29]:=

Out[31]=
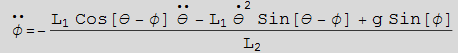
decouple the above 2 equations
In[32]:=
![]()
Out[33]=
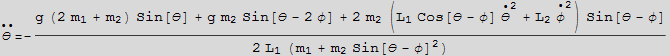
Out[34]=
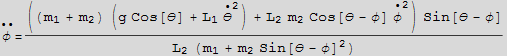
Numerically solve the 2 equations found above for θ(t) and φ(t), use some arbitrary parameters
In[38]:=
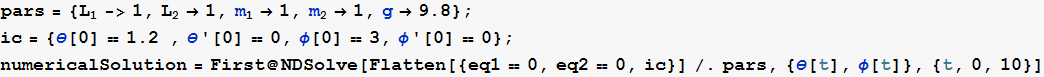
Out[40]=
![]()
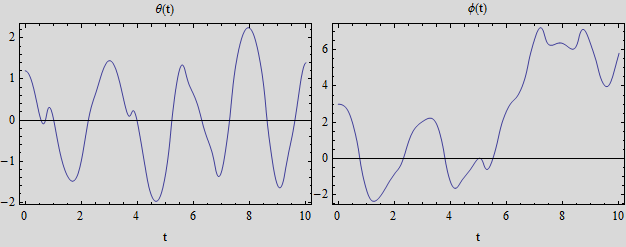
Make plots of the solutions. Assume ![]()
In[41]:=

Out[43]=
F=ma solution
Write the free body diagram
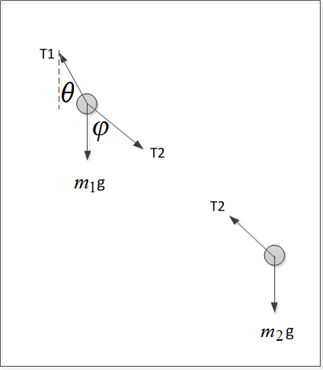
We have 4 unknowns ![]()
Write F=ma for forces radially along θ along for ![]()
![]()
![]()
Resolve forces perpendicular for ![]()
![]()
![]()
Write F=ma for forces radially along φ along for ![]()
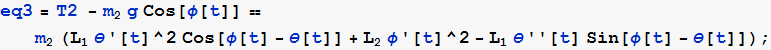
![]()
Resolve forces perpendicular for ![]()
![]()
![]()
Solve the above 4 equestions
![]()
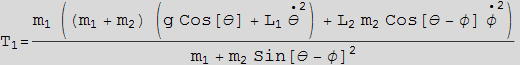
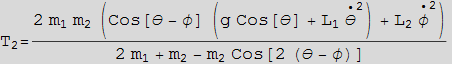
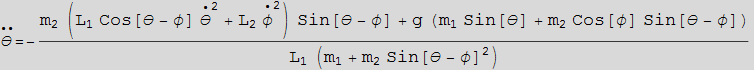
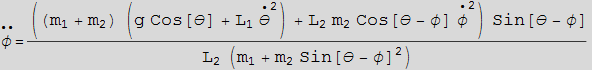
We see that the solution from F=ma is the same as the solution obtained from Lagrange method. To verify
![]()
![]()
![]()
![]()
We see from the above that the solutions are identical.