5.1 Example 1 (Stable limit cycle)

The following system of ode’s gives solutions that have limit cycle. \begin{align*} x'(t) &= -b y + a x (1-x^2-y^2)\\ y'(t) &= a x + b y (1-x^2-y^2)\\ \end{align*}

When \(a\) and \(b\) is not \(1\), then the solution shows more iterations until it reaches the limit cycle, which is a circle of radius \(1\).

The following animations are for different initial conditions (one inside the limit cycle and one outside) and for different values of \(a,b\).

As \(a\) becomes closer to zero, it takes many more cycles to appraoch the limit cycle.

\(a=0.15,b=2\) and initial conditions inside \(x(0)=0.15,y(0)=0.2\) Pause Play Restart Step forward Step back	\(a=0.15,b=2\) and initial conditions outside \(x(0)=2,y(0)=1.7\) 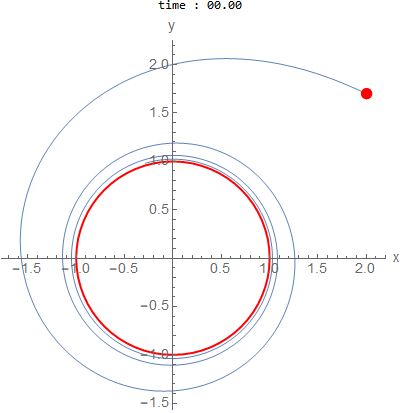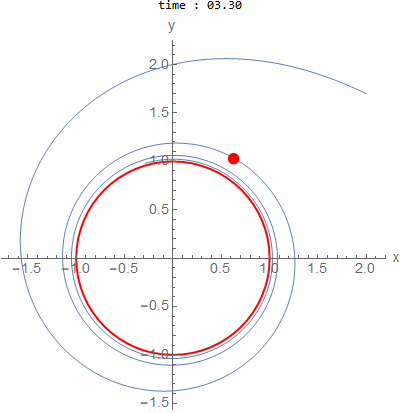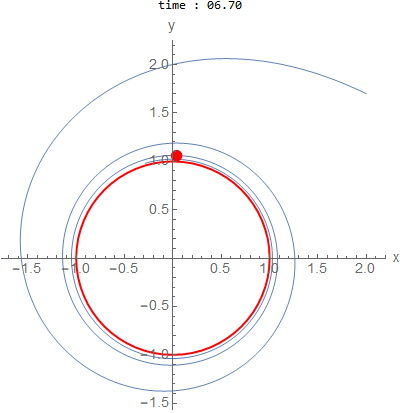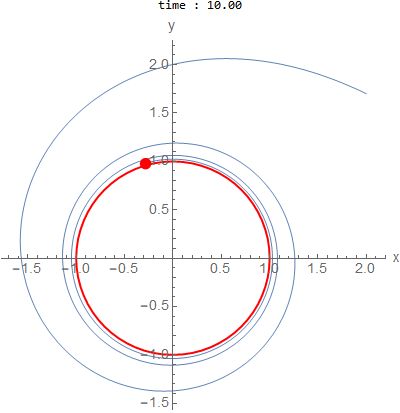Pause Play Restart Step forward Step back
\(a=0.05,b=2\) and initial conditions inside \(x(0)=0.15,y(0)=0.2\) Pause Play Restart Step forward Step back	\(a=0.05,b=2\) and initial conditions outside \(x(0)=2,y(0)=1.7\) 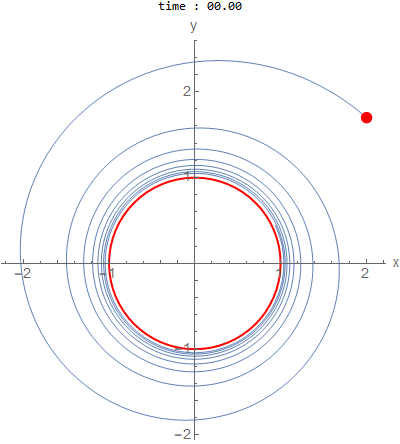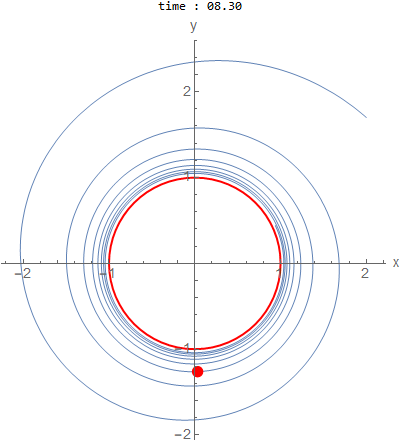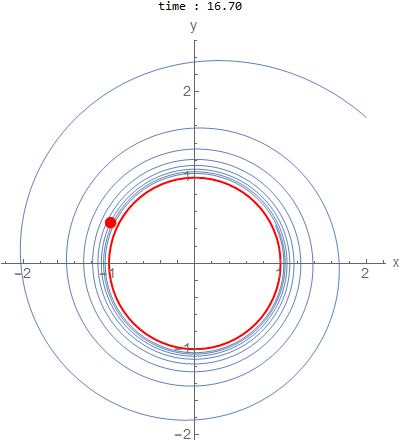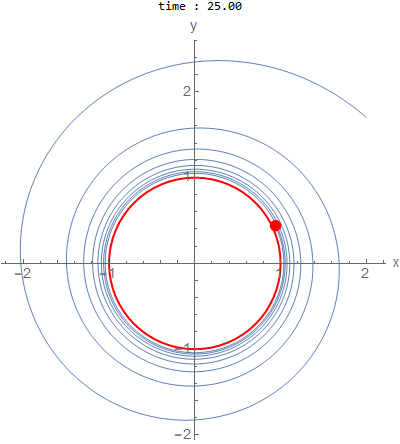Pause Play Restart Step forward Step back
\(a=1,b=1\) and initial conditions inside \(x(0)=0.15,y(0)=0.2\) Pause Play Restart Step forward Step back	\(a=1,b=1\) and initial conditions outside \(x(0)=2,y(0)=1.7\) 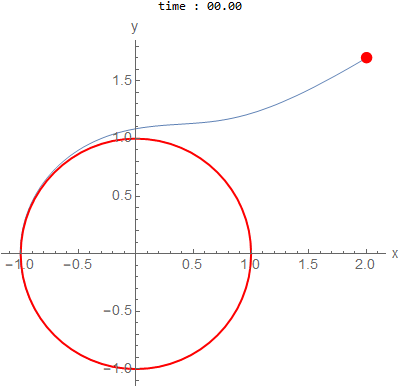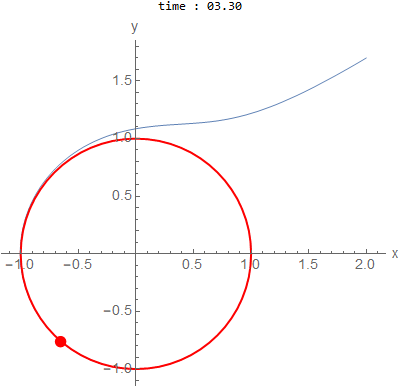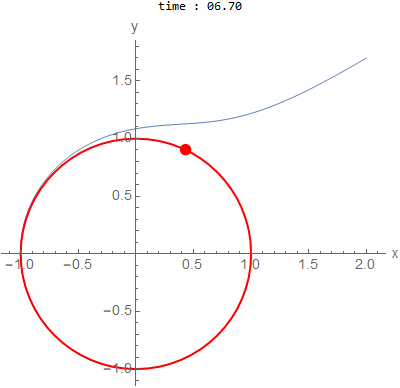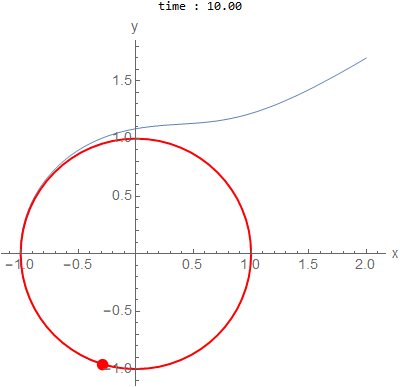Pause Play Restart Step forward Step back