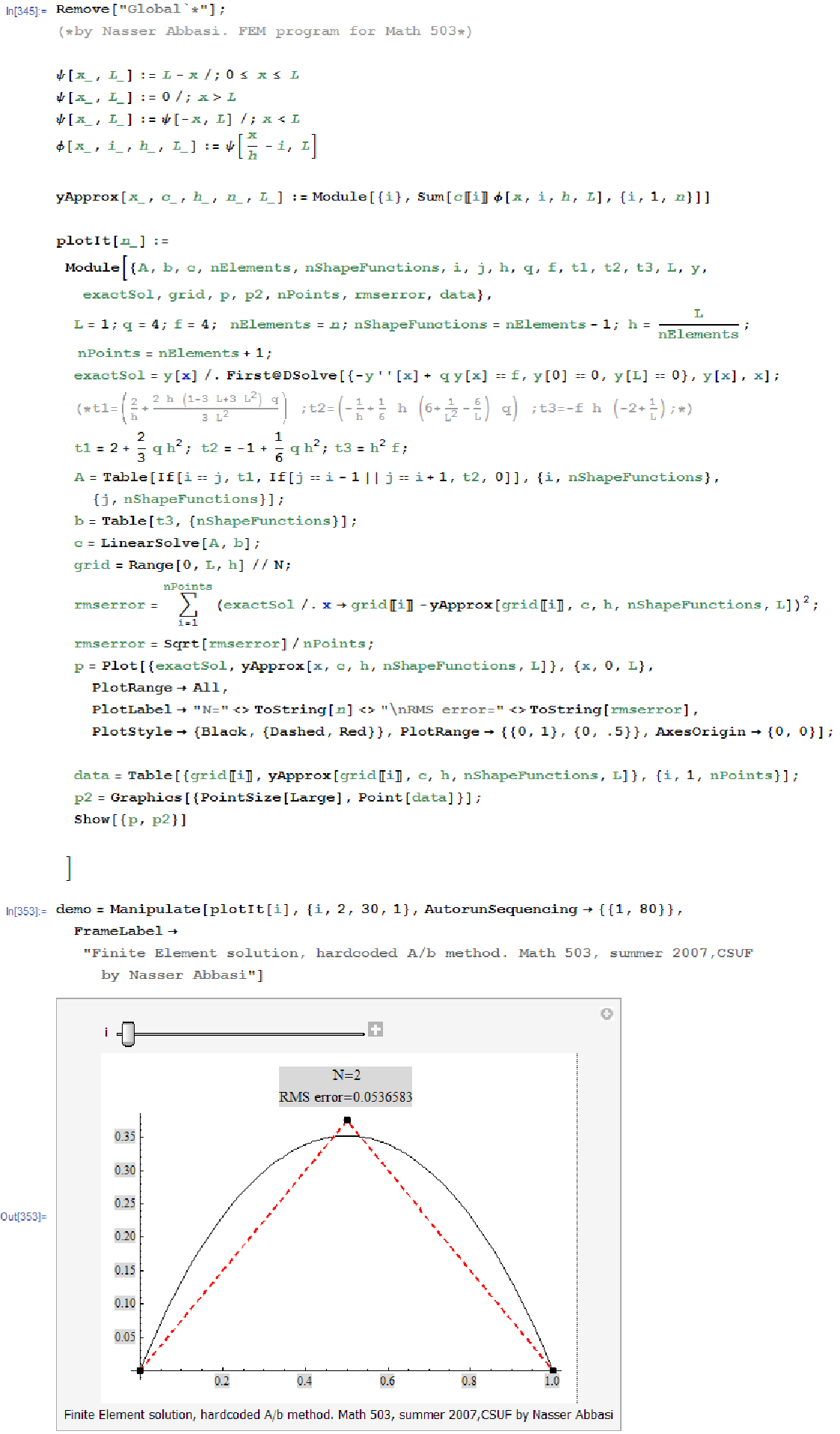
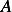 matrix and the
matrix and the 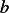 vector for the problem of
vector for the problem of 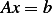 which is generated from the FEM formulation
for this project. I also include a very short Mathematica program which implements the FEM
solution.
which is generated from the FEM formulation
for this project. I also include a very short Mathematica program which implements the FEM
solution.
This is a suplement to the report for the computer project for Math 503. This includes the symbolic derivation
of the 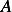 matrix and the
matrix and the 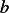 vector for the problem of
vector for the problem of 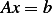 which is generated from the FEM formulation
for this project. I also include a very short Mathematica program which implements the FEM
solution.
which is generated from the FEM formulation
for this project. I also include a very short Mathematica program which implements the FEM
solution.
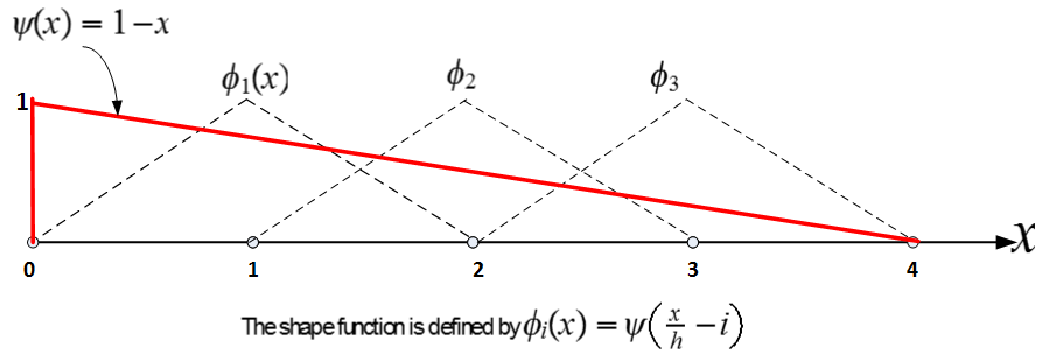
For ![x = [0,L]](in5x.png) where
where 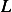 is the length, we define the shape functions (called tent function in this case) as
shown below
is the length, we define the shape functions (called tent function in this case) as
shown below
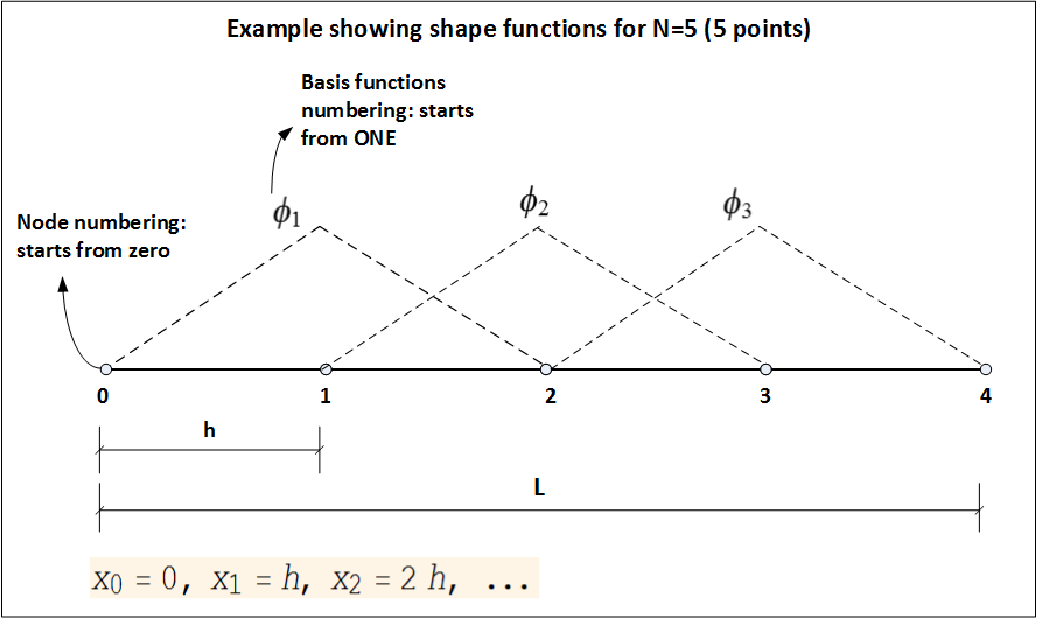
The shape function is defined by 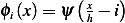 where
where
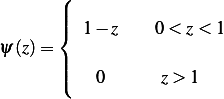 | (1) |
And 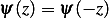 as shown in this diagram
as shown in this diagram
Now the derivative of 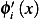 is given by
is given by
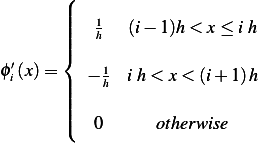
Now we write the weak form in terms of the above shape function (which is our admissible direction). From part 1 we had
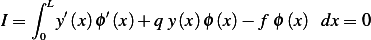
And Let
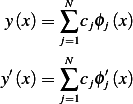
Hence, now we pick one admissible direction at a time, and need to satisfy the above integral for each of these. Hence we write
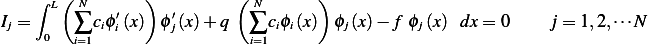
But due to sphere on influence of the  extending to only
extending to only  the above becomes
the above becomes
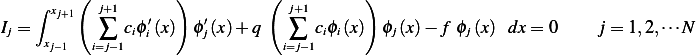
Hence we obtain 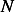 equations which we solve for the
equations which we solve for the 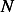 coefficients
coefficients 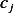
Now to evaluate 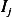 we write
we write
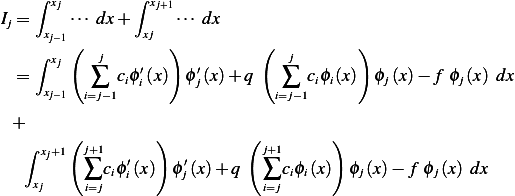
Now we will show the above for  which will be sufficient to build the
which will be sufficient to build the  matrix due to
symmetry.
matrix due to
symmetry.
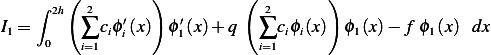
Hence breaking the interval into 2 parts we obtain
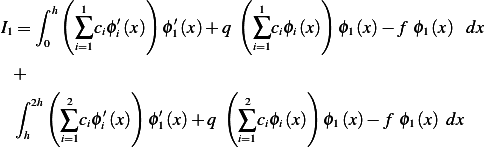
Hence
Now set up a little table to do the above integral.
![|-------|----|-----|-----------------|-------------------|
| | | | | |
|Range | ϕ′1 | ϕ′2 | ϕ1 | ϕ2 |
|-------|----|-----|-----------------|-------------------|
| [0,h] | 1 |N ∕A | ψ (− x+ 1)→ x | N∕A |
|-------|-h--|-----|------h-------h--|-------------------|
| | −1 | 1 | (x ) x | ( x ) x |
--[h,2h]---h-----h---ψ--h-− 1-→-2-−-h--ψ--−-h +-2-→-h −-1-|](in31x.png)
The above table was build by noting that for  it will have the equation
it will have the equation  when
when 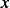 is under the
left leg of tent. And it will have the equation
is under the
left leg of tent. And it will have the equation 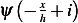 when
when 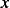 is under the right leg of the tent. This is
because for
is under the right leg of the tent. This is
because for 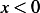 , the argument to
, the argument to 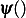 is negative and so we flip the argument as per the definition for
is negative and so we flip the argument as per the definition for 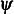 shown in the top of this report.
shown in the top of this report.
Hence we obtain for the integral in (2)
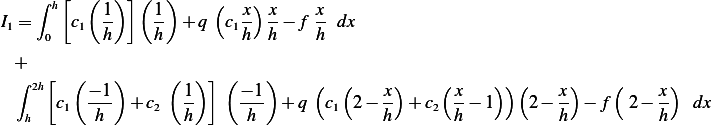
so the above becomes integral becomes
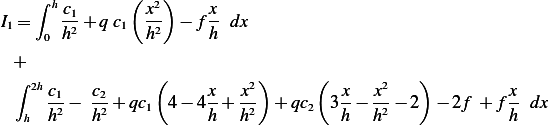
Hence
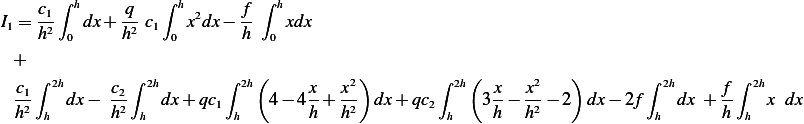
Which becomes
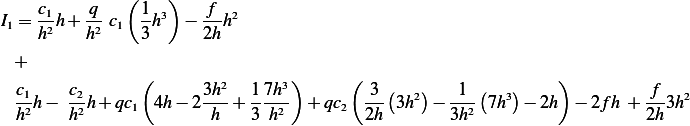
or
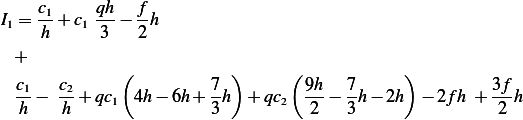
Therefore
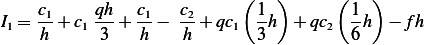
Hence
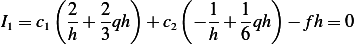
Multiply by 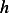 we obtain
we obtain
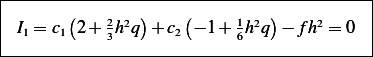 | (2) |
Hence we now can set up the  system using only the above equation by taking advantage that
system using only the above equation by taking advantage that 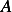 will be tridiagonal and there is symmetry along the diagonal.
will be tridiagonal and there is symmetry along the diagonal.
The following is the FEM program to implement the above, with few plots showing how close it gets to
the real solution as  increases.
increases.
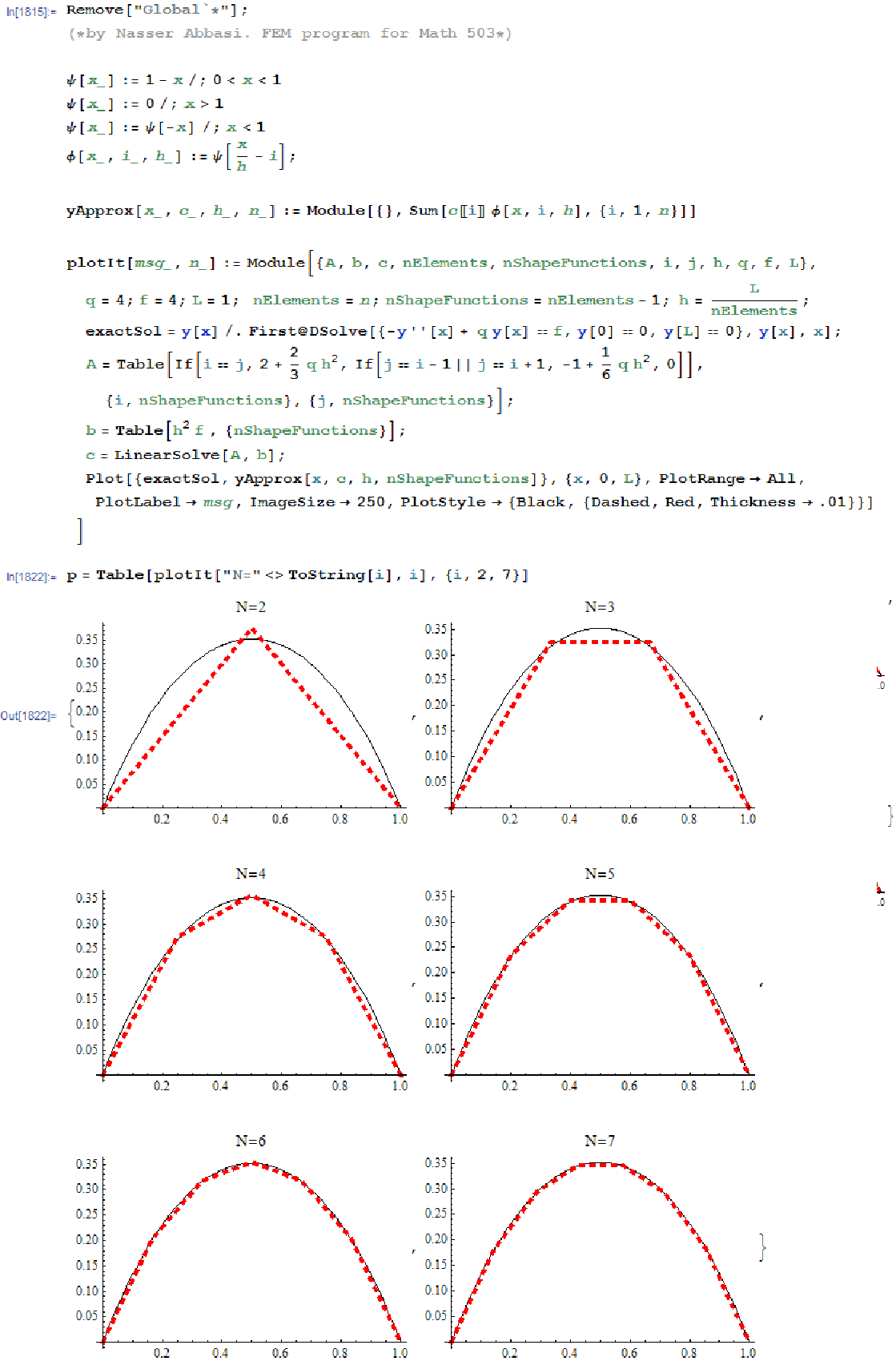
I also written a small Manipulate program to simulate the above. Here it is