Problem 2.12,
by Nasser Abbasi
Source code
function nma_HW_2_12(problemPart,x)
%function
nma_HW_2_12
%
% finds
the error in calculation of derivatives for a number
% of
functions as a function of delta, at some specific points
% using
the centered derivative formula
% f(t+TAO) - f(t-TAO)
% f'(t) = ---------------------
% 2 TAO
% INPUT
% problemPart : a character of the name of the part, a-e
% x : the value to evalute the derivative at.
%
% This
is the solution to problem 2.12, parts a-e.
%
%
%HW 5,
2.12 parts a-e
%Nasser
Abbasi, phy 240, Sam Jose State Univ.
%Feb 11,
2002
% struct
to hold the data as we iterate
struct err { ...
value : 0 ...
delta : 0 };
switch(problemPart)
case 'a'
deriveExact=2*x;
process('fa',problemPart,x,deriveExact);
return;
case 'b'
deriveExact=5*x^4;
process('fb',problemPart,x,deriveExact);
return;
case {'c','d','e'}
deriveExact=cos(x);
process('fc',problemPart,x,deriveExact);
return;
error('invalid part number');
end
%%%%%%%%%%%%%%%%%%%%%%%%%%
%
%
%%%%%%%%%%%%%%%%%%%%%%%%%%
function process(functionName,problemPart,x,exact)
delta =1;
for i=1:21
deriveApprox = (
feval(functionName,x+delta) - feval(functionName,x-delta)) / (2*delta);
err.value(i) =
abs(exact - deriveApprox);
err.delta(i) =
delta;
delta =
delta/10;
end
p=loglog(err.delta,err.value,'.');
title(sprintf('Showing abs error in evaluation of derivative for part
%c at x=%d',problemPart,x));
xlabel('Delta, or step size, drawn on a log scale.');
ylabel('Absolute error, drawn on a log scale');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
function x^2, for part a
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [y]=fa(x)
y=x^2;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
function x^5 for part b
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [y]=fb(x)
y=x^5;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
function sin(x) for part c
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [y]=fc(x)
y=sin(x);
Run output
» clear all
» help nma_HW_2_12
function nma_HW_2_12
finds the error in calculation of derivatives for a number
of functions as a function of delta, at some specific points
using the centered derivative formula
f(t+TAO) - f(t-TAO)
f'(t) = ---------------------
2 TAO
INPUT
problemPart : a character of the name of the part, a-e
x : the value to evalute the derivative at.
This is the solution to problem 2.12, parts a-e.
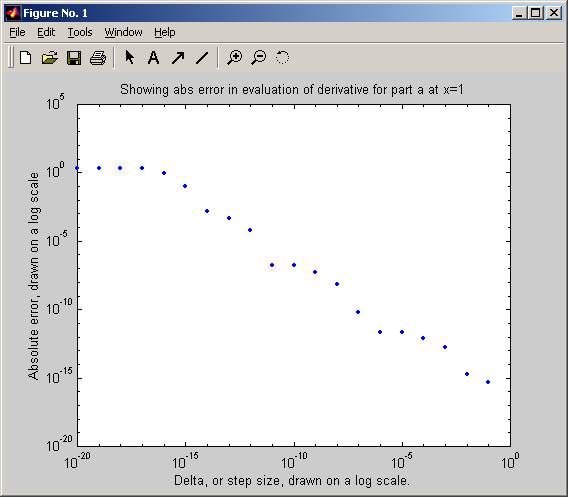
» nma_HW_2_12('a',1)
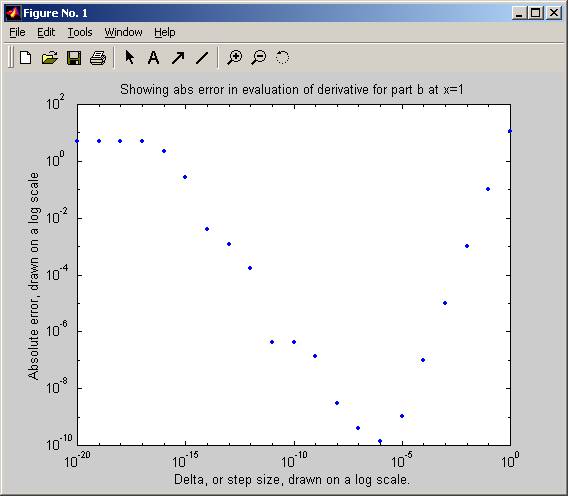
nma_HW_2_12('b',1)
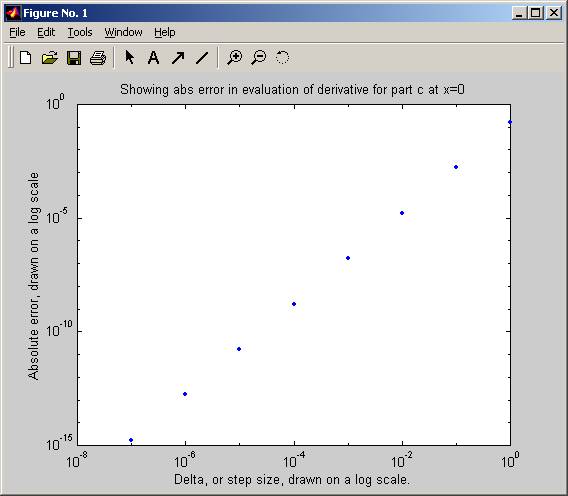
» nma_HW_2_12('c',0)
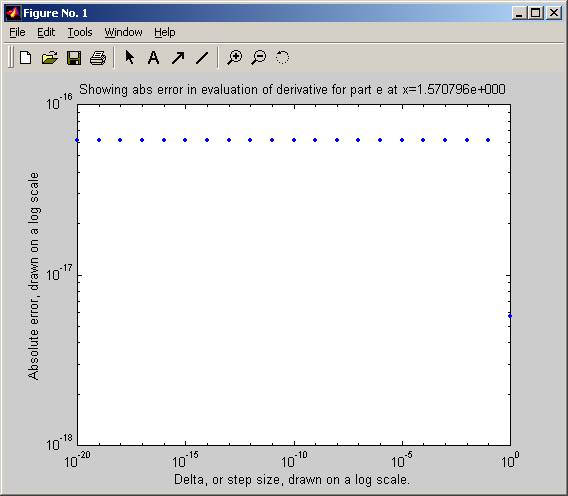
» nma_HW_2_12('d',pi/4)
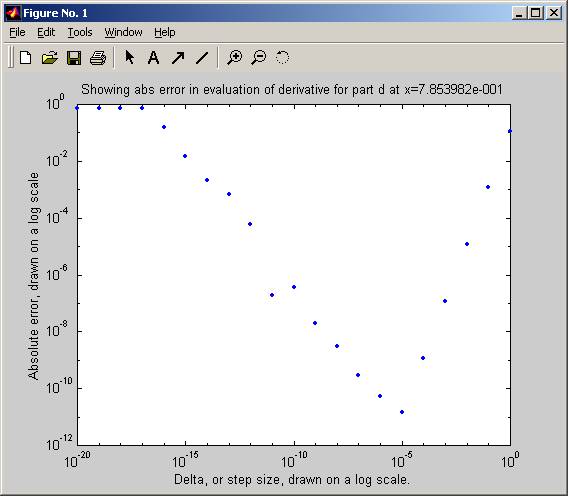
» nma_HW_2_12('e',pi/2)