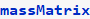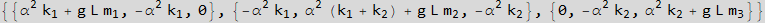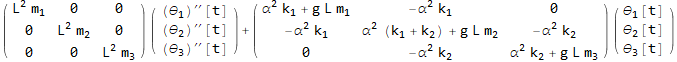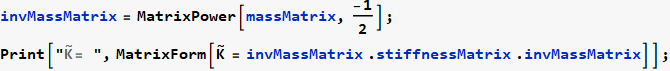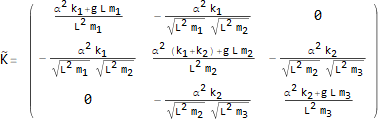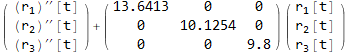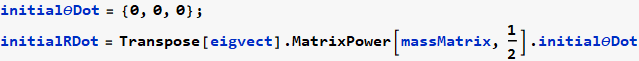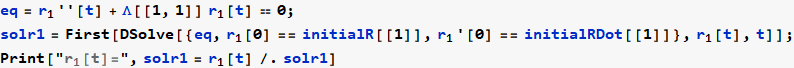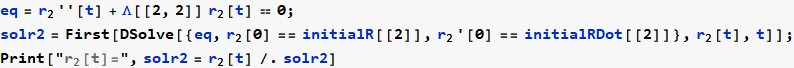Modal Analysis for 3 pendulum with springs problem

by Nasser M Abbasi

This small note computes the eigenvectors of a 3 degrees freedom by modal analysis and without modal analysis and analysis the difference between the aproaches.

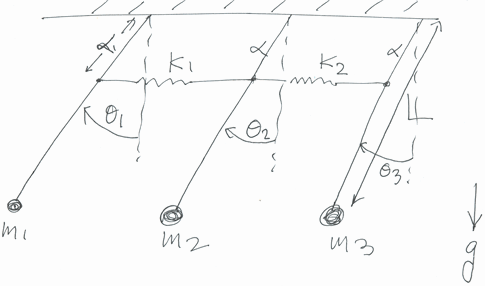
This digram below describes the problem. We use Lagrangian formulation to determine the equation of motions, then use modal analysis to decouple the system and solve it. In this system , the springs are attached at a distant α From the edge. Each pendulum has length L and has masses m1,m2,m3 attached to the end. To obtain a numerical solution, we assume some initial conditions such as  θ(0)={Pi/4,Pi/4,Pi/4} and 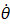={0,0,0}

Modal analysis by decoupling

First define some notations to use

Define a function which accepts the kinetic and potential energy and return back the stiffness and the mass matrix

Now define the kinetic and potenatial energy

Now call the above function to generate the stiffness and mass matrix. It also prints the 3 equations of motion

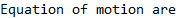
Now print the STIFFNESS and MASS matrix

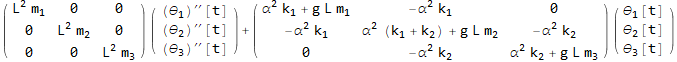
Now that we have the stiffness and mass matrix, we can perform modal analysis. Start by doing the first transformation

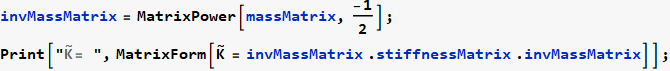
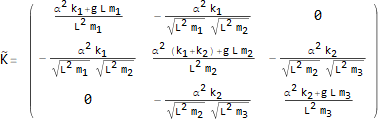
Now define some numerical values to use for the rest of the analysis amd generate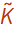

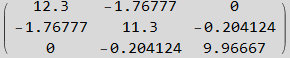
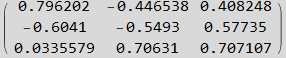
Now find Λ matrix

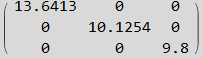
Hence the decoupled system of differential equations is

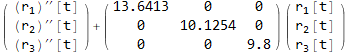
Now convert the IC from θ (t) space to r (t) space

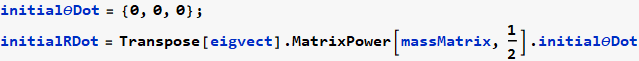
Now solve the r (t) system

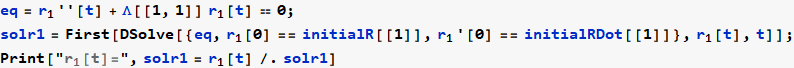
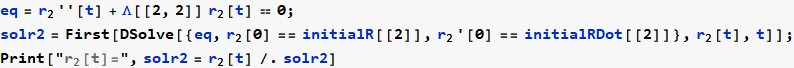
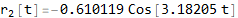
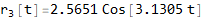
Now convert solution from r (t) to θ (t)

Now plot the solutions

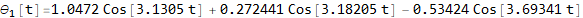
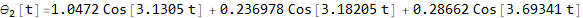
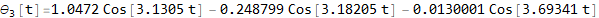
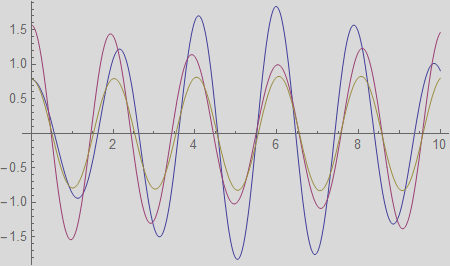
Modal analysis without decoupling