
Report on the derivation of the solid pendulum with mass-spring system demonstration
Nasser M. Abbasi, updated August 28, 2012
Physical description of the problem
The problem is described in the following diagram

A solid pendulum has a mass-less tube at the end of it with spring around it that has a bob at its end. Hence the mass-spring can only move in a horizontal direction inside the tube. There are 2 degrees of freedom for this system x(t) and θ(t) . The Lagrangian is derived for the case if a spring is present of not.
Derivation for the solid pendulum with the case when the spring is present
The kinetic energy KE is given by

![]()
and the potential energy is given by (assuming the pivot at zero potential, and negative potential is below that)
![]()
![]()
The Lagrangian is found and the differential equations derived

![]()
![]()
![]()
Parameters are given values, NDSolve is used to generate numerical solution
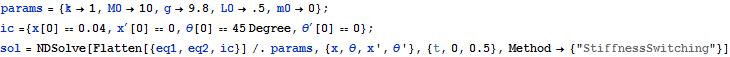
![]()
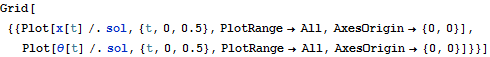
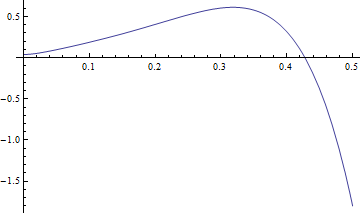 |
 |
Derivation for the solid pendulum with the case when spring is missing
The kinetic energy remain the same and is given by

![]()
and the potential energy is given by (assuming the pivot at zero potential, and negative potential is below that)
![]()
![]()
The Lagrangian is found and the differential equations derived
![]()
![]()
![]()
![]()
Parameters are given values, NDSolve is used to generate numerical solution
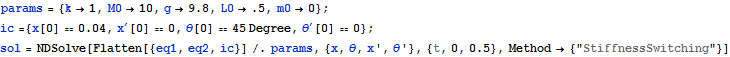
![]()

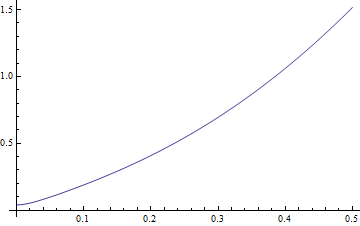 |
 |
Derivation for the massless pendulum with the spring present
This case was not part of the demo. But I include the model here for illustration. In this case, the pendulum is assumed massless. As follows

In this case, for some reason, singularity can be generated by NDSolve under some very specific conditions.
Kinetic energy
![]()
![]()
Potential energy
![]()
![]()
Lagrnagian is found and the 2 equations derived
![]()
![]()
![]()
![]()
NDSolve is used to solve and solution is plotted

![]()

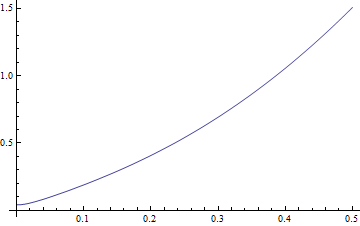 |
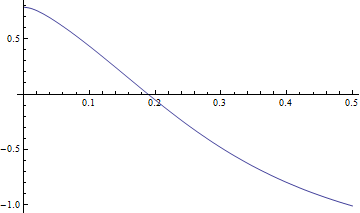 |
Singularity exist under some specific conditions. Needs more investigation

![]()
NDSolve::ndsz: