Intro to MATLAB symbolic features.

Collected from MATLAB demo with editing and new additions by Nasser M. Abbasi

% Introduction to the Symbolic Math Toolbox.

% The Symbolic Math Toolbox uses "symbolic objects" produced

% by the "sym" funtion. For example, the statement

x = sym('x');

% produces a symbolic variable named x.

% You can combine the statements

a = sym('a'); t = sym('t'); x = sym('x'); y = sym('y');

% into one statement involving the "syms" function.

syms a t x y

% You can use symbolic variables in expressions and as arguments to

% many different functions.

r = x^2 + y^2

r =

x^2+y^2

theta = atan(y/x)

theta =

atan(y/x)

e = exp(i*pi*t)

e =

exp(i*pi*t) % Notice that it did not evaluate numerically this expression since

% one term in it, the ‘t’, is symbolic. Even though ‘i’ and ‘pi’ are numeric.

% It is sometimes desirable to use the "simple" or "simplify" function

% to transform expressions into more convenient forms.

f = cos(x)^2 + sin(x)^2

f =

cos(x)^2+sin(x)^2

f = simple(f)

f =

% Derivatives and integrals are computed by the "diff" and "int" functions.

diff(x^3)

ans =

3*x^2

% Use pretty command to format the output of symbolic computation to make it easy

% to read

pretty(int(x^3))

1/4 x

pretty(int(exp(-t^2)))

1/2

1/2 pi erf(t)

% If an expression involves more than one variable, differentiation and

% integration use the variable which is closest to 'x' alphabetically,

% unless some other variable is specified as a second argument.

% In the following vector, the first two elements involve integration

% with respect to 'x', while the second two are with respect to 'a'.

[int(x^a), int(a^x), int(x^a,a), int(a^x,a)]

ans =

[ x^(a+1)/(a+1), 1/log(a)*a^x, 1/log(x)*x^a, a^(x+1)/(x+1)]

% You can also create symbolic constants with the sym function. The

% argument can be a string representing a numerical value. Statements

% like pi = sym('pi') and delta = sym('1/10') create symbolic numbers

% which avoid the floating point approximations inherent in the values

% of pi and 1/10. The pi created in this way temporarily replaces the

% built-in numeric function with the same name.

pi = sym('pi')

pi =

delta = sym('1/10')

delta =

1/10

s = sym('sqrt(2)')

s =

sqrt(2)

% Conversion of MATLAB floating point values to symbolic constants involves

% some consideration of roundoff error. For example, with either of the

% following MATLAB statements, the value assigned to t is not exactly one-tenth.

t = 1/10, t = 0.1

t =

0.1000

t =

0.1000

% The technique for converting floating point numbers is specified by an

% optional second argument to the sym function. The possible values of the

% argument are 'f', 'r', 'e' or 'd'. The default is 'r'.

% 'f' stands for 'floating point'. All values are represented in the

% form '1.F'*2^(e) or '-1.F'*2^(e) where F is a string of 13 hexadecimal

% digits and e is an integer. This captures the floating point values

% exactly, but may not be convenient for subsequent manipulation.

sym(t,'f')

ans =

'1.999999999999a'*2^(-4)

%'r' stands for 'rational'. Floating point numbers obtained by evaluating

% expressions of the form p/q, p*pi/q, sqrt(p), 2^q and 10^q for modest sized

% integers p and q are converted to the corresponding symbolic form. This

% effectively compensates for the roundoff error involved in the original evaluation,

% but may not represent the floating point value precisely.

sym(t,'r')

ans =

1/10

% If no simple rational approximation can be found, an expression of the form

% p*2^q with large integers p and q reproduces the floating point value exactly.

sym(1+sqrt(5),'r')

ans =

7286977268806824*2^(-51)

% 'e' stands for 'estimate error'. The 'r' form is supplemented by a term

% involving the variable 'eps' which estimates the difference between the

% thoretical rational expression and its actual floating point value.

sym(t,'e')

ans =

1/10+eps/40

sym(pi,'e')

ans =

pi-198*eps/359

% 'd' stands for 'decimal'. The number of digits is taken from the current

% setting of DIGITS used by VPA. Fewer than 16 digits looses some accuracy,

% while more than 16 digits may not be warranted.

digits(15)

sym(t,'d')

ans =

.100000000000000

digits(25)

sym(t,'d')

ans =

.1000000000000000055511151

% The 25 digit result does not end in a string of 0's, but is an accurate

% decimal representation of the floating point number nearest to 1/10.

% MATLAB's vector and matrix notation extends to symbolic variables.

n = 4;

A = x.^((0:n)'*(0:n))

A =

[ 1, 1, 1, 1, 1]

[ 1, x, x^2, x^3, x^4]

[ 1, x^2, x^4, x^6, x^8]

[ 1, x^3, x^6, x^9, x^12]

[ 1, x^4, x^8, x^12, x^16]

D = diff(log(A))

D =

[ 0, 0, 0, 0, 0]

[ 0, 1/x, 2/x, 3/x, 4/x]

[ 0, 2/x, 4/x, 6/x, 8/x]

[ 0, 3/x, 6/x, 9/x, 12/x]

[ 0, 4/x, 8/x, 12/x, 16/x]

% Example to display irrational numbers to an arbitrary precision

>> vpa(pi,100)

ans =

3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117068

>> vpa(sqrt(2),100)

ans =

1.414213562373095048801688724209698078569671875376948073176679737990732478462107038850387534327641573

Plotting functions for symbolic expressions:

Ezplot, ezcontour, ezcontourf, ezmesh, ezmeshc, ezplot3, ezpolar, ezsurf, ezsurfc

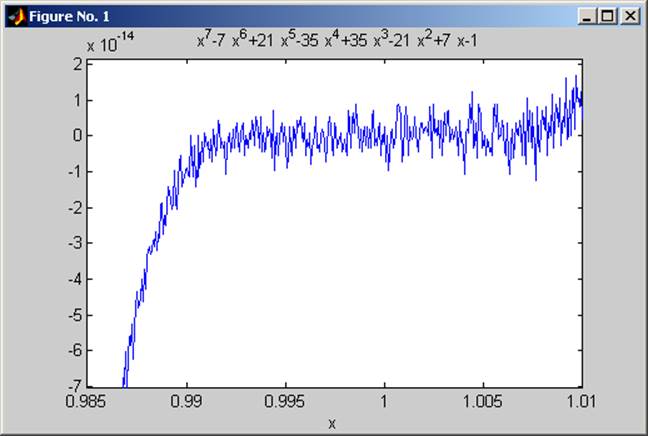
>> ezplot(' x^7-7*x^6+21*x^5-35*x^4+35*x^3-21*x^2+7*x-1',[0.985,1.01])

MATLAB commands related to symbolic manipulation

Sym

Syms

subs

SUBEXPR Rewrite in terms of common subexpressions.