eps is the smallest difference between floating point numbers that the machine can recognize. It is defined as the smallest floating point value that when added to 1.0 will produce a floating point number different from 1.0.

» help eps

EPS Floating point relative accuracy.

EPS returns the distance from 1.0 to the next largest

floating point number. EPS is used as a default tolerance by

PINV and RANK, as well as several other MATLAB functions.

» isequal( (1+eps)-1,0)

ans =

» isequal( (1+eps/2)-1,0)

ans =

» eps

ans =

2.220446049250313e-016

%to see it in full decimal format, do

>> fprintf('%.40f',eps)

0.0000000000000002220446049250313100000000

12345678901234567890123456789012

digit 16

Q4. Do I need to declare a variable before using it?

No. In Matlab there is no syntax for variable declaration. When you type ‘a=10’, matlab creates the variable ‘a’ and gives it the type ‘double’ by default.

Q5. is matlab case sensitive?

Matlab variables and functions are case sensitive. This means variable A is different from variable a. Example:

>> clear all

>> A=10;

>> A

A =

>> a

??? Undefined function or variable 'a'.

Q6. How to remove a variable from my workspace?

Use the command ‘delete’ to completely remove a variable from the workspace. For example, to remove variable called ‘a’, then type ‘delete a’. To remove all variables from workspace use the command ‘delete all’. It is a good idea to do ‘delete all’ before starting a new run of your program while testing to make sure you do not use an old variable value or the wrong variable by mistake.

Q7. How to use symbolic matlab to solve one equation for one unknown or N equations for N unknowns?

Use the command ‘solve’ which solves a set of equations.

From matlab help

>> help solve

SOLVE Symbolic solution of algebraic equations.

SOLVE('eqn1','eqn2',...,'eqnN')

SOLVE('eqn1','eqn2',...,'eqnN','var1,var2,...,varN')

For example, to solve for ‘x’ in the equation x^2+2*x+1=0, use the command

>> S=solve('x^2+2*x+1')

S =

[ -1]

The roots are put in a column vector S.

To solve a set of equations, say 2 equations in 2 unknowns, say x+y-4=0, 3*y+x-10=0, write the equations each inside a string, and then write the names of the unknowns in the order desired to get them back in the result as shown below:

S=solve('x+y-4','3*y+x-10','x','y')

S =

x: [1x1 sym]

y: [1x1 sym]

>> S.x

>> S.y

So, x=1, y=3 is the solution.

Q8. How to compare if 2 floating point numbers are equal?

One tricky thing about using floating points is the fact that some numbers can not be represented exactly inside the computer hardware.

In normal math, when do ‘0.42 – 0.5 + 0.08’ the result is obviously 0. nothing more and nothing less.

But since 0.42 and 0.08 can not be represented exactly in IEEE floating point format, we get the following wrong result from pure mathematics point of view:

>> fprintf('%.40f', 0.42 - 0.5 + 0.08)

-0.0000000000000000138777878078144570000000

You see that the result is not the mathematical zero.

Now, change the order of the terms, and now we get a different result (the correct one this time)

>> fprintf('%.40f', 0.42 +0.08 - 0.5)

0.0000000000000000000000000000000000000000

Notice that the error in the first computation is actually less the EPS (the machine accuracy tolerance):

>> fprintf('%.40f', eps)

0.0000000000000002220446049250313100000000

I’ll put EPS on top of the first result to see this more clearly

0.0000000000000002220446049250313100000000

-0.0000000000000000138777878078144570000000

What all this means is that we need to be very careful when we compare 2 floating points number.

If we have

N = 0.42 - 0.5 + 0.08

M = 0.42 + 0.08 - 0.5

And we try to compare N and M above expecting to get a result that indicates that the numbers are equal, instead we will get a different result. This can be disastrous to the numerical application if the algorithm we doing this comparison to decide on what logic to perform next. This example below illustrates this:

>> N = 0.42 - 0.5 + 0.08

N =

-1.387778780781446e-017

>> M = 0.42 +0.08 - 0.5

M =

>> if(N==M)

disp('Numbers are equal');

else

disp('Numbers are NOT equal');

end

Numbers are NOT equal

Instead, do the floating point comparison as follows:

>> if( abs(N-M) < eps )

disp ('Numbers are equal');

else

disp('Numbers are NOT equal');

end

Numbers are equal

The expression

‘if (a==b)’

should be replaced with

‘if( abs(a-b) < eps)’

almost always when working with floating point numbers.

So, to check if a floating point number is zero, use

‘if( abs(a) < eps)’

The point of this is that we want to see if the absolute difference between the 2 floating point numbers is within the EPS of the machine. If so, then we declare these number to be mathematically equal, even though they might have different bit pattern representation.

Q9. How to numerically solve Ax=b?

One way is to use the ‘\’ operator. Example:

>> A=[ 1 1; -3 -6]

A =

1 1

-3 -6

>> b=[-0.5;5]

b =

-0.5

>> x=A\b

x =

0.666666666666666

-1.16666666666667

Q 10. How to multiply 2 matrices element-by-element?

If A and B are matrices, then typing

C = A * B;

Does the normal matrix multiplication. If however you want to multiply each element in A by the corresponding element in B instead, then use the ‘.’ Operator as in:

C = A .* B;

For example:

>> A=[1 2; 3 4]

A =

1 2

3 4

>> B=[5 6; 7 8]

B =

5 6

7 8

>> C=A*B

C =

19 22

43 50

>> C=A .* B

C =

5 12

21 32

Q 11. How to find the size of a matrix?

Given a matrix A, then to find the number of rows do

row = size(A,1);

To number the number of columns do

col = size(A,2);

To obtain the number of rows and number of columns in one call do

[row,col] = size(A);

do help size for more info.

Q 12. How to put 2 plots on the same figure?

In matlab, when you issue the command ‘plot’, it will create a new figure window and then put the plot in that figure (assuming no figure already exist).

When you issue the plot command again, it will erase the earlier plot and use the same existing figure window to display the second plot.

It is sometimes useful to display both plots on the same figure (for example to compare one curve to the other). to do this, use the command ‘hold on’ after the first plot command. This causes matlab to keep the first plot (hold it on) when it plots the second plot. The command ‘hold on’ remains in effect until you issue the command ‘hold off’. This is an example to plot the sin(x) and cos(x) on the same figure.

>> x=[-pi:0.1:pi];

plot(x,sin(x)); hold on; plot(x,cos(x),'--')

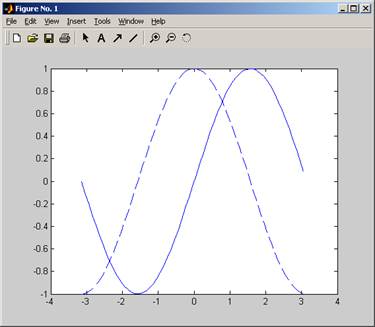
see help plot for more info.

Q 13 How to display a table of function values?

Suppose you want to display a table, that contains 2 columns. The first is the ‘x’ values and the second is the ‘y’ values. One easy way to do this is like this:

>> x=[-pi:0.1:pi]; <--- generate the ‘x’ values

>> y=sin(x); <--- generate the ‘y’ values

>> [x' y'] <--- display side by side. Notice the transpose

ans =

-3.14159265358979 -1.22464679914735e-016

-3.04159265358979 -0.0998334166468284

-2.94159265358979 -0.198669330795062

-2.84159265358979 -0.29552020666134

-2.74159265358979 -0.389418342308651

etc..

Q 14 How to display specific column or row in a matrix?

Use the ‘:’ operator.

For example, A(:,3) will be the third column of A.

A(1:3,:) will be the first 3 rows of A

Q 15 How to enter matrices in matlab

The following answer is copied from http://www.mines.utah.edu/~ggcmpsem/matlab/matlab.html

A good matlab tutorial.

MATLAB works with essentially only one kind of object, ie. a rectangular numerical matrix with possibly complex entries; all variables represent matrices. In some situations,
1-by-1 (1 x 1) matrices are interpreted as scalars and matrices with only one row (1 x n) or one column (m x 1) are interpreted as vectors.

Matrices can be introduced into MATLAB in several different ways:

1. Entered by an explicit list of elements

2. Loaded from external data files (see User's Guide)

3. Generated by built-in statements and functions

For example, either of the statements

A = [1 2 3; 4 5 6; 7 8 9]

and

A = [

1 2 3

4 5 6

7 8 9 ]

creates the obvious 3-by-3 matrix and assign it to a variable A.

Q 16 How to numerically ask matlab to find a root of a function?

Use the function ‘fzero’

From help fzero:

Examples

FUN can be specified using @:

X = fzero(@sin,3)

returns pi.

X = fzero(@sin, 3, optimset('disp','iter'))

returns pi, uses the default tolerance and displays iteration

information.

FUN can also be an inline object:

X = fzero(inline('sin(3*x)'),2);

Q 17 How to find the minimum of a function over some range?

Use fminsearch.

[X,FVAL]= FMINSEARCH(...) returns the value of the objective function,

described in FUN, at X.

Example:

>> [h,the_min] = fminsearch(@sin,pi)

h =

4.71238898038469

the_min =

-1

Q 18 How to numerically solve ODE in matlab?

Use matlab ode45. do help ode45. Also see on-line demos.

Q 19 How to sum elements of an array?

From matlab on-line help:

x = [1 2 3 4 5]; <--- the sum of element is 15.

% Do add up all the elements of x, use this:

y = sum(x)

% which is better than this:

y = 0;

for i=1:length(x)

y = y+x(i);

endy =

Q 20 does matlab have RECORD or STRUCT as in pascal and C?

Yes.

From matlab on-line help

You can construct a structure simply by assigning values to its fields. With these commands, we create the structure we've depicted.

patient.name = 'John Doe';

patient.billing = 127.00;

patient.test = [79 75 73; 180 178 177.5; 172 170 169];

patient =

name: 'John Doe'

billing: 127

test: [3x3 double]

the variable ‘patient’ is now a struct.

Q 21 What is in the signal processing tool box?

See the on-line help.

The Signal Processing Toolbox is a collection of tools built on the MATLAB technical computing environment. The toolbox provides two categories of tools:

Command line functions in the following categories:

1. Analog and digital filter analysis

2. Digital filter implementation

3. FIR and IIR digital filter design

4. Analog filter design

5. Filter discretization

6. Spectral Windows

7. Transforms

8. Cepstral analysis Statistical signal processing and spectral analysis Parametric modeling

9. Linear Prediction

10. Waveform generation

Q 22 Where to get more matlab help?

Matlab has an extensive on-line help.

>> help

HELP topics:

matlab\general - General purpose commands.

matlab\ops - Operators and special characters.

matlab\lang - Programming language constructs.

matlab\elmat - Elementary matrices and matrix manipulation.

matlab\elfun - Elementary math functions.

matlab\specfun - Specialized math functions.

matlab\matfun - Matrix functions - numerical linear algebra.

matlab\datafun - Data analysis and Fourier transforms.

matlab\audio - Audio support.

matlab\polyfun - Interpolation and polynomials.

matlab\funfun - Function functions and ODE solvers.

matlab\sparfun - Sparse matrices.

matlab\graph2d - Two dimensional graphs.

matlab\graph3d - Three dimensional graphs.

matlab\specgraph - Specialized graphs.

matlab\graphics - Handle Graphics.

matlab\uitools - Graphical user interface tools.

matlab\strfun - Character strings.

matlab\iofun - File input/output.

matlab\timefun - Time and dates.

matlab\datatypes - Data types and structures.

matlab\verctrl - Version control.

matlab\winfun - Windows Operating System Interface Files (DDE/COM)

winfun\comcli - (No table of contents file)

matlab\demos - Examples and demonstrations.

toolbox\local - Preferences.

toolbox\compiler - MATLAB Compiler

toolbox\optim - Optimization Toolbox

signal\signal - Signal Processing Toolbox

signal\sigtools - Filter Design & Analysis Tool (GUI)

signal\sptoolgui - Signal Processing Toolbox GUI

signal\sigdemos - Signal Processing Toolbox Demonstrations.

toolbox\stats - Statistics Toolbox

toolbox\symbolic - Symbolic Math Toolbox.

MATLAB6p5\work - (No table of contents file)

For more help on directory/topic, type "help topic".

For command syntax information, type "help syntax".

There are also on-line demos. Type help ‘demo’

There are zillions of matlab tutorials on the web. Go to google and type matlab tutorial.

For example:

http://www.mit.edu/~pwb/cssm/

Mathworks own web site has the full documentation of matlab on-line as well.

Q 23 Control system diagram

This diagram from the book signal processing using matlab

Q 24 How to brighten or darken an image?

Must convert it to double, then multiply (to brighten) by some scalar, then convert back to uint8

m=imread('Picture.png')

n=double(m(:,:,:));

n=n*2;

n=uint8(n);

image(n)