Hastings - Metropolis Algorithm implementation

by Naser Abbasi. Mathematics 504, Spring 2008. CSUF

This below is an implementation of the Hastings - Metropolis algorithm. A simple GUI interface allows the user to specify the number of steps to run the algorithm for. At each step, the current P matrix and the current calculated stationary distribution for this P matrix are shown to help observe the convergence.

The input to this run below is that of example 8.3.1 from Lecture notes of Math 504 by Professor B. Gearhart, CSUF. Below I show the user interface, and few screen shots showing the progress of the convergence to the final P matrix.

Few seed the random number generator and display the q and the π distribution used

In[1]:=

Out[2]//MatrixForm=

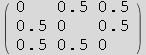
In[3]:=

Out[3]//MatrixForm=

In[9]:=

Out[9]=

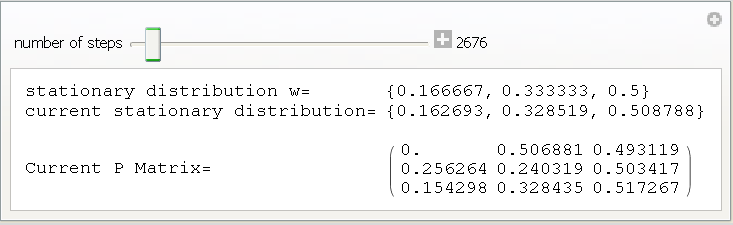
This a snap shot of the above output for number of iterations

Appending

Algorithm implementation

In[4]:=

Function to calculate β (x, y)

In[5]:=

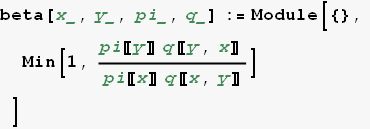
Function called at the end of the run to generate P from the path of states travelled

In[6]:=

Function to sample from q using uniform distribution

In[7]:=

The Hastings algorithm main loop

In[8]:=

Created by Wolfram Mathematica 6.0 for Students - Personal Use Only  (10 April 2008)