Mathematica for signal processing
By Nasser Abbasi, updated 1/21/2008
I started using Mathematica package called “signals and systems” version 1.2.1, which I bought around 2005 from WRI web site.
These are documentation from that package
Introduction chapter PDF
Analyzing signals chapter PDF
Filter design chapter PDF
Transforms chapter PDF
Representing signals and systems chanpter PDF
In addition, I collected all the commands in that package below

![]()
![]()
![]()



![]()
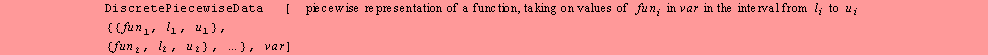
![]()
![]()

![]()
![]()



![]()



Options
specific to the analysis function.

![]()


Options specific to MagnitudePhasePlot.


Options for PoleZeroPlot.
![]()
![]()
![]()
Representing
analog filters.

Objects
for specifying the magnitude response of a filter.
![]()

Allowed
types of filters for analog filter design.
![]()
Option to DesignAnalogFilter.
![]()

Frequency
transformations of an analog filter object.

Some common mappings for use with AnalogFilterTransformation.
![]()
Finding
the DC gain.
![]() Representing an analog tapped delay line.
Representing an analog tapped delay line.
![]()
Representing
a digital IIR filter.

Methods
for converting an analog prototype filter into a digital filter.
![]()
Representing
a digital FIR filter.

Functions
for assisting in the design of two-dimensional decimation systems.
![]()
Options for DesignDecimationSystem2D.

The

Options for LaplaceTransform.
![]()
Option
specific to the inverse

The
Fourier transform and its inverse.

The
Z transform and its inverse.

Options for ZTransform.

Options
for inverse Z transform.

The
discrete-time Fourier transform and its inverse.

The
discrete Fourier transform and its inverse.

Options for DiscreteFourierTransform and InverseDiscreteFourierTransform.
![]()
Special
syntax for transforming a numeric vector.
![]()
Determining
stability from a transform object.
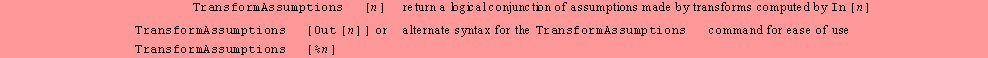
Assumptions
made by transforms during a computation.

Functions
for extracting parts of transform objects.

Data
objects resulting from forward transforms.

The
transform-based equation solvers.

Options
for the solving functions.
![]()
Functions
to perform convolution.
![]()
Options
for convolution.
![]()
Functions
for animating convolution by the "flip-and-slide" technique.
![]()
Functions
for autocorrelation.
![]()
Functions
to perform cross-correlation.
![]()
Functions
for working with intervals.
![]()
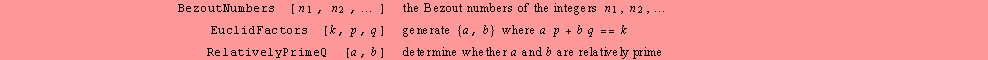

Functions
generating particular polynomials.

Functions
for manipulating polynomials and rational polynomials.

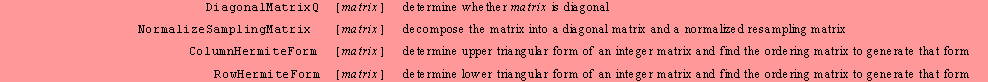
General
matrix operations.
Functions
to determine information about resampling matrices.

Functions
for finding common multiples and divisors of resampling matrices.

Operations
on resampling matrices.
![]()
Function
for computing various Smith form matrices.

Options
for Smith form decomposition.
![]()
Decomposing
a matrix based on a precomputed Smith form.
![]()
The option for ConstrainedSmithFormDecomposition.

Computations
with polygons.

![]()


Options for WritePtolemySimulation.
![]()
A
signal simplification function
![]()
Options to SimplifySignal.
![]()
![]()
![]()
This is an example using it To
find discrete fourier transform
assume
we have signal {3,2,1,0,1,2}, period N=6, then write
t=DiscreteFourierTransform[SampledData[{3,2,1,0,1,2},1,n],6,n,k]
![]()
The result is correct but need to divide by N

To
extract the stuff I am interested in do:
