Final Project Design. MAE 146
Nasser Abbasi
June 5, 2003
Correcting
LEO orbit inclination choices
When
to inject from LEO to GEO
Orbit
design final decision tree
Rocket
Design program algorithm. Serial staging
Rocket
design calculation results
Summary
of design parameters and report conclusion
Rocket
design run output. From earth to final position. Computer program output
Abstract
An orbit solution is found to
minimize the ![]() . A number of choices were considered to find the best method
to correct the parking orbit inclination, and a number of choices considered to
find the best time to inject to GEO from LEO.
. A number of choices were considered to find the best method
to correct the parking orbit inclination, and a number of choices considered to
find the best time to inject to GEO from LEO.
The solution includes a partial
inclination correction of the parking orbit and it includes a limited waiting
in LEO orbit to minimize ![]() required in GEO to rendezvous with the first satellite.
Phase-wait looping was used in GEO to maneuver the probe to meet with the
second satellite and to move the probe to its final position.
required in GEO to rendezvous with the first satellite.
Phase-wait looping was used in GEO to maneuver the probe to meet with the
second satellite and to move the probe to its final position.
A decision tree showing the
options considered for the orbit design is shown with the reasons why an option
was not selected. The total ![]() was found to be 4.41508 km/sec and the duration to reach
final position was 4 days and 21 hrs and 57 minutes.
was found to be 4.41508 km/sec and the duration to reach
final position was 4 days and 21 hrs and 57 minutes.
For the rocket design, 4 staging options considered (single stage with single engine, serial staging with single engine per stage, cluster staging, and parallel staging).
Serial staging with single engine per stage was selected. The rocket was designed to reach final position starting from earth and not from LEO. Real commercial rocket engines selected for the purpose of using their ISP values.
A Matlab computer program was
written to design the rocket based on optimization of fuel distribution among
the different stages. This theory is based on using lagrange multiplier. In
addition, the program uses a list of ![]() values that it will
try in order to find the value that minimizes the total fuel mass.
values that it will
try in order to find the value that minimizes the total fuel mass.
20 different values of ![]() were iterated over for
each stage. The program tries 1,2 or 3 stages, and will select the number of
stages based on the cost of adding a stage compared to the amount of fuel
saving gained by adding the stage. If the saving in fuel is less than 5%
compared to not adding a stage, then it is felt that adding the extra stage is
not warranted. The complexity of adding an extra stage is not worth the small
amount of fuel saving.
were iterated over for
each stage. The program tries 1,2 or 3 stages, and will select the number of
stages based on the cost of adding a stage compared to the amount of fuel
saving gained by adding the stage. If the saving in fuel is less than 5%
compared to not adding a stage, then it is felt that adding the extra stage is
not warranted. The complexity of adding an extra stage is not worth the small
amount of fuel saving.
Design starts from the last segment of the flight trip going backwards to the surface of the earth. For the sequence from GEO to the final position, no staging was used, but a single rocket engine with calculated sufficient fuel used.
Final rocket design uses 2 stages to go from LEO to GEO, and one engine with sufficient calculated fuel to reach final position.
Introduction
The following shows the spacecraft when it first reached LEO
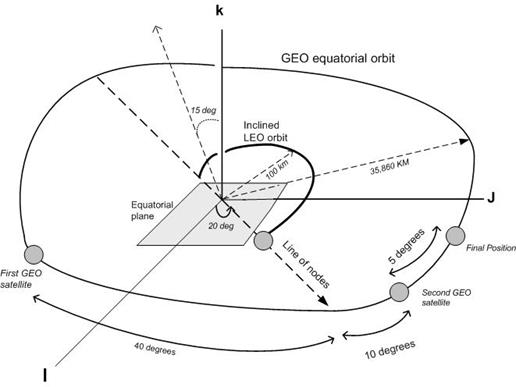
The goal is to reach final position with minimal ![]() . Next, a rocket was designed to achieve this with minimal
fuel.
. Next, a rocket was designed to achieve this with minimal
fuel.
Orbit design analysis
Correcting LEO orbit inclination choices
The following are the options considered to correct the inclination
- First perform a Hohmann transfer to transfer from the
inclined LEO orbit to an inclined GEO orbit, and then apply all of the
plane inclination correction at the apogee of the Hohmann elliptical orbit
where the ellipse speed will be smallest. This is less costly in ΔV
than the above sequence, and is a common maneuver.
- Apply a small and partial plane inclination
correction (say an angle α) at the perigee of the Hohmann orbit, then
apply the remaining inclination correction (angle β-α) at the
apogee. Notice that for α=0, this case becomes the same as case (2)
above.
- Correct all of the plane inclination before performing a Hohmann transfer from LEO to GEO. In other words, all of the inclination correction is made at the perigee of the Hohmann ellipse where the Hohmann transfer speed is largest. This will turn out to be the most fuel costly maneuver.
Performing needed calculation of ΔV using the above 3 options showed that second option is the best (least ΔV) . α=1.288 and β=13.7. Diagram below shows the partial correction geometry.
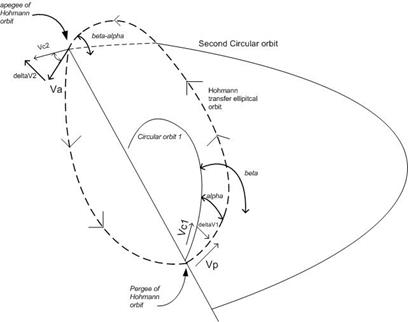
When to inject from LEO to GEO
Next, the choices as to when to inject from LEO to GEO are considered.
- Inject
from the top end of the lines of nodes. Reach GEO orbit and then phase-wait in that orbit to
rendezvous with the target.
- loop-wait
in the LEO orbit until the correct lead angle β with the target is reached. Calculate this for
when the spacecraft is on the top end of the lines of nodes. (must be at
either end of the lines of nodes to inject to GEO)
- The same
as above, but for the case when the spacecraft is on the bottom end of the lines of nodes.
- loop-wait in the LEO orbit until the lead angle is closest to β the first time this happens before the first full GEO orbit is made by the 1st satellite. This is a trade-off between choice 1 and 2,3.
Calculations showed option 4 above to be the best in terms of ΔV and time considerations. Probe does full 6 orbits in LEO before injecting to GEO. This resulted is smallest ΔV to apply when in GEO to phase-wait for 1st satellite.
To complete the trip to final position:
- Probe now in GEO and after reaching 1st satellite, makes one phase-wait orbit to rendezvous with the 2nd satellite. Calculations showed that making more than one phase-wait orbit costs too much time for the small saving in ΔV.
- Probe locks to 2nd satellite for one full GEO orbit then makes one phase-wait orbit to reach final position. Calculations showed that making more than one phase-wait orbit costs too much time for the small saving in ΔV.
Summary of orbit design are shown next.
|
Sequence |
ΔV(km/sec) |
Duration (sec) |
|
Wait in LEO |
0 |
50,050 |
|
Hohmann transfer |
4.0716 |
18,916 |
|
Rendezvous with 1st target |
0.0598 |
83,770 |
|
Rendezvous with 2nd target |
0.255 |
98,131 |
|
Lock with 2nd target |
0 |
86,400 |
|
Position to final destination |
0.02868 |
87,360 |
|
TOTAL |
4.41508 |
424,627 |
|
|
|
117.95 hrs = 4 days 21 hrs 57 min |
Orbit design final decision tree
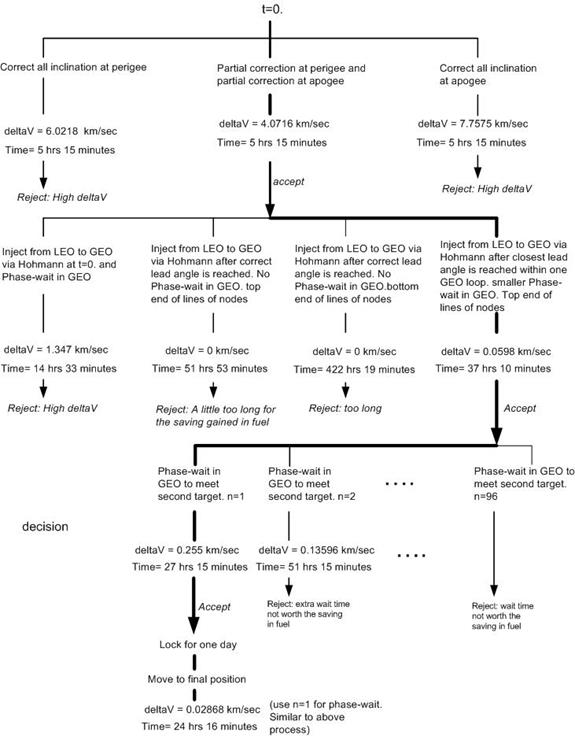
Earth to LEO orbit design
Next, I considered adding earth to LEO orbit. This below is the analysis of this part.
- To
reach LEO, we have found that V_leo=7.844 km/sec. To be more realistic, we
need to account for the gravitational loss and drag. Typical
time to reach LEO is about 2 minutes or 120 seconds. Hence additional
ΔV to account for gravity loss is gΔt=9.8(120)=1176 m/sec =1.176
km/sec.
- For
the drag effect, it of course depends on the rocket cross sectional area,
the drag coefficient and air density. A typical value I have seen in the
literature for typical rockets is to use 5% of the LEO velocity to account
for drag. Hence an additional ΔV for drag will be 5% of 7.844 km/sec
or 0.392 km/sec.
- Hence
total ΔV to reach LEO = 7.844+1.176+0.392=9.412 km/sec
- Final ΔV from earth to final probe position is shown in next diagram.
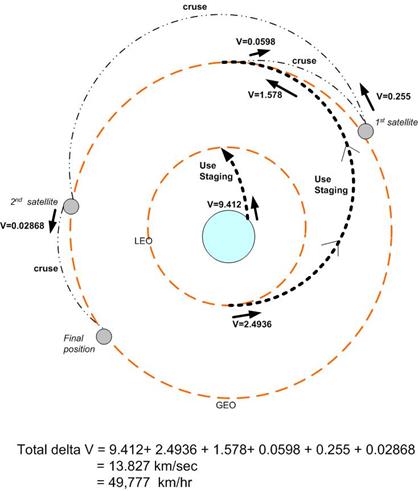
Rocket design analysis
Staging options
Staging options considered are:
- One
stage, single rocket engine. Least complex, but least efficient in terms
of amount of load it can carry. Waste of extra fuel. (Special case of
serial staging design below, when n=1).
- Serial
staging with a single rocket engine per stage. Consider 1 or 2 or 3 stages
stacked on top of each others. More efficient, but does not provide as
much thrust as parallel staging or clustered engines.
- Clustered
design. More than one engine fired at the same time. Can be used in single
or multiple stages. Adds more thrust. But clustering is usually done at
lower stages (left off stage) where the extra thrust is needed. 2,3 or 4
engines are typically clustered together.
- Parallel staging. Shuttle is best example. Extra solid fuel rocket boosters added to the sides of an existing rocket to increase left-off thrust. Discarded shortly after left off. Parallel staging is used for lower staging only (earth to LEO). For upper staging (LEO to GEO) it is not consider needed due to lower thrust requirements Hence will not be considered here for the LEO to GEO design.
Serial staging was selected. Option 4 above was not selected as that option is used only for earth to LEO where high thrust is needed. Here we are asked to design a LEO to GEO rocket design only. Second option was not considered again for same reasons. The extra clustered engines are needed for high thrust conditions at left off.
The core of the design is an algorithm that accepts as input the following: current payload, the ΔV for the current trip sequence, and a list of ε to use for each stage, and a list of Isp's to use for each stage, and of course, the number of stages to design for. It returns the amount of fuel (mp) and the ms to use for each stage distributed such that this total is the most optimal (minimum) possible for the whole rocket.
The above algorithm is based on optimization theory using Lagrange multiplier as described in the book Orbital Mechanics by Prussing and Conway.
Rocket design using optimization theory based on Lagrange multiplier. Solved numerically using a trial and error method.
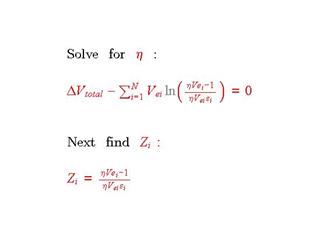
Total ΔV is calculated to be 13.827 km/sec. (From orbit design).
Research the net for rocket engines to use. Obtain an idea of what current and reasonable Isp's to use. Learn what rocket engines where used and in which stages. Which engines are used for lower stages (earth to LEO) and which engines are used for upper stages (LEO to GEO). Select the engines to use from the list to be shown next. Reference:
Rocket Engines Selected
The following are the list of rocket engine found which I needed to select from.

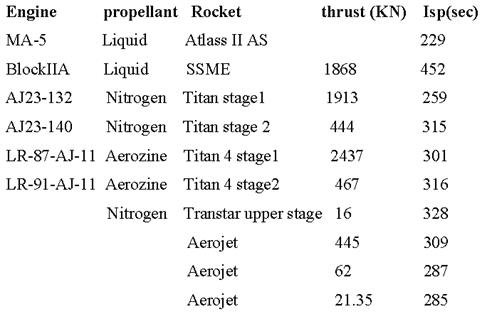

As above, select a range of reasonable values of ε (structural mass ratio) to use. Call this the list of ε.
Engines selected: For upper stages (LEO to GEO). For stage1 use IUS
SRM-1 from Boeing, a Solid rocket motor with
a thrust of 185.1 KN and Isp 295.5 secs. For stage 2 use IUS SRM-2 with
thrust 78.41 KN and ISP 289.1 sec.
For final GEO maneuvering use rocket engine RL10B-2 from Pratt&Whitney,
an LO1/H2 liquid engine with a thrust of 111 KN and Isp 462.
For earth to LEO: Use Titan4 first stage LR-87-AJ-11 Nitrogen engine
with Isp 301. For second and third stage use Titan4 LR-91-AJ-11 with Isp 316.
Make a list of the above engines. Run the MATLAB design program to design the rocket for one or two or three stages. Look at the output and decide how many stages to use based on the cost benefit of adding additional stages for the fuel saving gained.
Design starts from the last segment of the flight trip going backwards to the surface of the earth.
For the sequence from GEO to the final position, no staging was used, but a single rocket engine RL10B-2 (Isp=462) with calculated sufficient fuel used.
Going backwards, for trip n, optimal mp and ms was found. mp+ms was then added to the payload for the purpose of finding the ms and mp of trip n-1.
For the trip from LEO to GEO, the optimization algorithm was applied to try for 1,2, or 3 stages with the selected engines from before.
For the trip from earth to LEO, the optimization algorithm was applied to try for 1,2, or 3 stages with the selected engines.
Upper stages (LEO to GEO) Isp list : [295.5 289.1 289.1]
Lower stages (earth to LEO) Isp list: [301 316 316]
ε list : 20 values evenly spaced between 0.08 to 2.0 were tried.
Final GEO stages. Isp=462.
Rocket Design program algorithm. Serial staging
LEO to GEO:
try one stage. Use Isp=295.5, ε list. Solve for mp and Z using the optimization algorithm for one stage by trying for each value of ε list.
try 2 stages. Use Isp=[295.5 289.1] , ε list. Solve for mp and Z using optimization algorithm for two stages.
try 3 stages. Use Isp=[295.5 289.1 289.1 ] , ε list. Solve for mp and Z using optimization algorithm for three stages.
Ask: How much reduction in total mp we obtained from going from one stage to 2 stages? Is reduction worthwhile? (> 5-10% ?) If so, then ask the same question for going from 2 stages to 3 stages. Based on this, select the number of stages to use.
Earth to LEO:
try one stage. Use Isp=301, ε list. Solve for mp and Z using the optimization algorithm for one stage.
try 2 stages. Use Isp=[301 316] , ε list. Solve for mp and Z using optimization algorithm for two stages.
try 3 stages. Use Isp=[301 316 316 ] , ε list. Solve for mp and Z using optimization algorithm for three stages.
How much reduction in total mp we obtained from going from one stage to 2 stages? Is reduction worthwhile? (> 5-10% ?) If so, then ask the same question for going from 2 stages to 3 stages. Based on this, select the number of stages.
Rocket design calculation results
Results of the design are shown next. First trying one stage from LEO to GEO
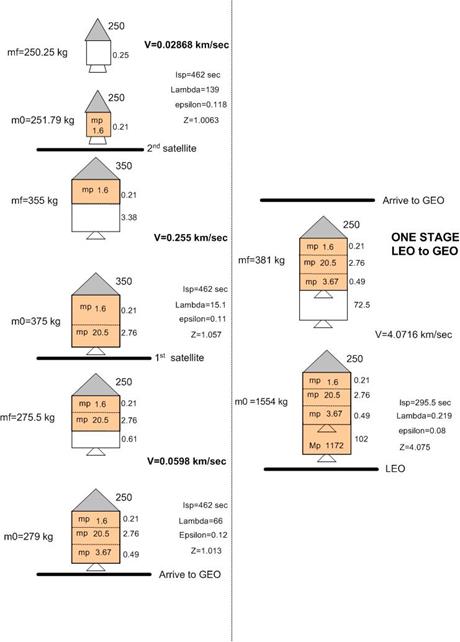
Next, try 2 stages from LEO to GEO
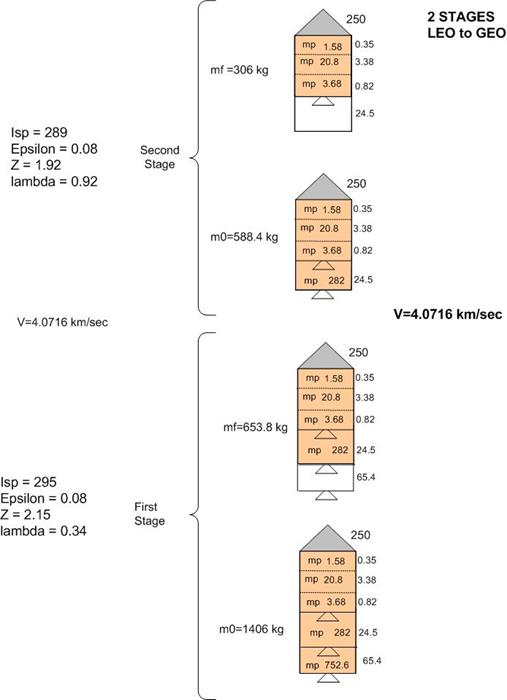
For 3 stages LEO to GEO, program result found the total rocket mass to be 1377 kg with total fuel taking 1007 kg. For 2 stages LEO to GEO, we saw that the total rocket mass was 1406 kg with fuel taking 1034 kg. Hence by adding one more stage we only save 27 kg of fuel, or about 2.5 %. This saving is not worth the extra complexity and cost of an additional stage. Hence will use only 2 stages for the LEO to GEO.
Next, the design of the earth to LEO will be shown. For this, use the rocket mass of 1406 kg as the payload for the design of earth to LEO rocket.
For a one stage earth to LEO, no solution was found using Isp 301 with any value of ε from 0.08 to 2.0 broken into 20 different values.
For 2 or 3 stages, solutions where found and is shown below.
For 2 stages, total rocket mass was 69,174 kg with fuel taking 62,345 kg of that.
For 3 stages, total rocket mass was 51,078 kg with fuel taking 45,696 kg of that. We see that here adding a 3rd stage results in a saving of about 30% of fuel. Hence for earth to LEO, 3-stage solution was selected.
Summary of design parameters and report conclusion
Orbit design: total ![]() km/sec. 9.412 km/sec is for earth to LEO, and the rest for
LEO to final position. Partial orbit correction is used.
km/sec. 9.412 km/sec is for earth to LEO, and the rest for
LEO to final position. Partial orbit correction is used.
Rocket design: For earth to LEO, serial staging is used. 3 stages. Each with single rocket engine.
Earth to LEO rocket specification:
First stage: ![]() 0.08, Isp=301 sec,
mp=30,519 kg,
0.08, Isp=301 sec,
mp=30,519 kg, ![]() 0.04239
0.04239
First stage: ![]() 0.08, Isp=316 sec,
mp=11,855 kg,
0.08, Isp=316 sec,
mp=11,855 kg, ![]() 0.109137
0.109137
First stage: ![]() 0.08, Isp=316 sec, mp=
3,322 kg,
0.08, Isp=316 sec, mp=
3,322 kg, ![]() 0.3894
0.3894
LEO to GEO rocket specification:
First stage: ![]() 0.08, Isp=295.5 sec,
mp=752.5 kg,
0.08, Isp=295.5 sec,
mp=752.5 kg, ![]() 0.344
0.344
First stage: ![]() 0.08, Isp=289.1 sec,
mp=282 kg,
0.08, Isp=289.1 sec,
mp=282 kg, ![]() 0.918
0.918
The above parameters achieve the design goal set at the start of reaching final position with the minimal fuel. Performing partial orbit correction, and using optimization theory based on lagrange multiplier have achieved the objective set at the start.
References
- Orbital mechanics. Prussing and Conway.
- Space flight dynamics, 2nd edition byWiesel.
- http://www.spaceandtech.com/spacedata/engines/rd180_sum.shtml for rocket engine database
- Lecture notes, MAE 146 by Professor Melissa Orme
- Nasa web site for general rocket related information.
Appendix
Rocket design run output. From earth to final position. Computer program output



Matlab source code
function lagrange =
nma_rocket_getLagrangeMultiplier(deltaV,Ve,epsilon)
%function nma_rocket_getLagrangeMultiplier(deltaV,Ve,epsilon)
%
%Solves equation 5.57 in the book orbital mechanices
page 96, by
%Prussing and Conway
%
%Finds the lagrange multipler to optimize fuel
distribution for a
%multistage rocket.
%
%Input:
% deltaV: The
total velosity increment for the rocket. in km/sec
%
% Ve: A
vector whose elements are the effective exhaust velosity in km/sec.
% Ve =
Isp*g
% Watch
out. Ve must be in km/sec.
% so for
an Isp=300 seconds, Ve= 300*9.8066/1000
%
% epsilon: A
vector whose elements are the epsilon for each rocket stage.
% This
is the structural mass ratio defined as (ms/(mp+ms)) where
%
ms=structural mass, mp=fuel mass
%
%OUTPUT:
% the
lagrange multiplier value.
% Use this
to find the Z's as per equation 5.56 in the above book
%
%Author: Nasser Abbasi
%June 1, 2003
lagrange = 0.5;
tol =
0.0001;
g =
9.8066;
OVER = 1;
UNDER = 0;
TRUE = 1;
FALSE = 0;
maxIter =
1000;
delta =
0.05; % by how much to start adjustment
to lagrange each time
lastCheck =
OVER;
lastLagrange = lagrange;
firstTime = TRUE;
iterCounter=0;
while(1)
lastLagrange = lagrange;
% lagrange
iterCounter=iterCounter+1;
if(iterCounter>maxIter)
error('Failer to find lagrange multiplier');
end
sum = 0;
for(i=1:length(Ve))
c = Ve(i);
Z
= (lagrange*c -
1)/(lagrange*c*epsilon(i)) ;
if(Z<0)
error('Complex result for log. Check data, unable to solve');
end
sum =
sum + c * log(Z);
end
% sum
% deltaV
if(abs(sum-deltaV)<tol)
return;
end
if(
deltaV-sum < 0 )
if(firstTime)
firstTime = FALSE;
lagrange = lagrange-delta;
else
if( lastCheck == UNDER )
lagrange = lagrange-delta;
else
delta = delta/2;
lagrange = lagrange - delta;
end
end
lastCheck = UNDER;
else
if(firstTime)
firstTime = FALSE;
lagrange = lagrange+delta;
else
if( lastCheck == OVER )
lagrange = lagrange+delta;
else
delta = delta/2;
lagrange = lagrange + delta;
end
end
lastCheck = OVER;
end
end
function nma_rocket_design()
%function nma_rocket_design()
%
% design rocket from earth to GEO
% final project MAE 146
%
% Nasser Abbasi
%
FALSE=0;
TRUE=1;
g=9.80666;
Isp=[462];
epsilon=linspace(0.08,2,20);
Ve=zeros(length(Isp),1);
for(i=1:length(Isp))
Ve(i)=Isp(i)*g/1000; % in
km/sec
end
deltaV=0.02868; % km/sec, from design project I.
last step
mL=250;
minTotalMass = Inf;
bestVe =
0;
bestEpsilon =
0;
bestZ =
0;
bestLambda =
0;
bestMp =
0;
bestMs =
0;
%one stage only for this step
SOLVED=FALSE;
for(i=1:length(Ve))
for(j=1:length(epsilon))
try
lagrange =
nma_rocket_getLagrangeMultiplier(deltaV,Ve(i),epsilon(j));
[Z,mp,ms,lambda]=nma_rocket_mutliStageSolutionLagrange(lagrange,Ve(i),epsilon(j),mL);
SOLVED=TRUE;
totalMass=sum(mp)+sum(ms)+mL;
if( totalMass <= minTotalMass)
minTotalMass = totalMass;
bestVe = Ve(i);
bestEpsilon = epsilon(j);
bestZ = Z;
bestLambda = lambda;
bestMp = mp;
bestMs = ms;
end
catch
end
end
end
if(~SOLVED)
error('Failed to solve for 2nd satellite to final position\n');
end
fprintf('*********** from 2nd satellite to final
position **********\n');
if(minTotalMass>0)
fprintf('deltaV=%f\n',deltaV);
fprintf('min total mass=%f kg\n',minTotalMass);
fprintf('m0 = %f kg\n',mL+bestMp+bestMs);
fprintf('mf = %f kg\n',mL+bestMs);
fprintf('best Ve=%f km/sec \n',bestVe);
fprintf('best Isp=%f sec\n',bestVe/g * 1000);
fprintf('best Epsilon=%f \n',bestEpsilon);
fprintf('best Z =%f \n',bestZ);
fprintf('best lambda=%f \n',bestLambda);
fprintf('best mp =%f \n',bestMp);
fprintf('best ms =%f \n',bestMs);
else
fprintf('Failed to find any one stage that will meet deltaV with given
Isp\n');
fprintf('Please increase number of stages of increase Isp or reduce
payload\n');
end
%step before last. Use same rocket engine found
above since no staging
deltaV=0.255; % km/sec, from design project I. last
step
mL=250+100+bestMp+bestMs;
lagrange =
nma_rocket_getLagrangeMultiplier(deltaV,bestVe,bestEpsilon);
[Z,mp,ms,lambda]=nma_rocket_mutliStageSolutionLagrange(lagrange,bestVe,bestEpsilon,mL);
fprintf('********* from 1st satellite to second
satellite\n');
fprintf('deltaV=%f\n',deltaV);
fprintf('m0 = %f kg\n',mL+mp+ms);
fprintf('mf = %f kg\n',mL+ms);
fprintf('mp=%f \n',mp);
fprintf('ms=%f \n',ms);
fprintf('lambda=%f \n',lambda);
fprintf('Z=%f \n',Z);
fprintf('Ve=%f \n',bestVe);
fprintf('Isp=%f \n',bestVe/g*1000);
fprintf('epsilon=%f\n',bestEpsilon);
%step before that. use same rocket engine.
deltaV=0.0598; % km/sec, from design project I. last
step
mL=mL+mp-100+ms;
%remove the 100 kg
lagrange =
nma_rocket_getLagrangeMultiplier(deltaV,bestVe,bestEpsilon);
[Z,mp,ms,lambda]=nma_rocket_mutliStageSolutionLagrange(lagrange,bestVe,bestEpsilon,mL);
fprintf('********* from Geo arrival to second
satellite\n');
fprintf('deltaV=%f\n',deltaV);
fprintf('m0 = %f kg\n',mL+mp+ms);
fprintf('mf = %f kg\n',mL+ms);
fprintf('mp=%f \n',mp);
fprintf('ms=%f \n',ms);
fprintf('lambda=%f \n',lambda);
fprintf('Z=%f \n',Z);
fprintf('Ve=%f \n',bestVe);
fprintf('Isp=%f \n',bestVe/g*1000);
fprintf('epsilon=%f\n',bestEpsilon);
minTotalMass = Inf;
bestVe =
0;
bestEpsilon =
0;
bestZ =
0;
bestLambda =
0;
bestMp =
0;
bestMs =
0;
mL=mL+mp+ms;
Isp=[295.5];
Ve=zeros(length(Isp),1);
for(i=1:length(Isp))
Ve(i)=Isp(i)*g/1000; % in
km/sec
end
%one stage try
deltaV=4.0716; % km/sec, from design project I. last
step
for(j=1:length(epsilon))
try
lagrange = nma_rocket_getLagrangeMultiplier(deltaV,Ve(1),epsilon(j));
[Z,mp,ms,lambda]=nma_rocket_mutliStageSolutionLagrange(lagrange,Ve(1),epsilon(j),mL);
totalMass=sum(mp)+sum(ms)+mL;
if( totalMass <= minTotalMass)
%fprintf('totalMass=%f, j=%d, i=%d\n',totalMass,j,i);
minTotalMass = totalMass;
bestVe = Ve(1);
bestEpsilon = epsilon(j);
bestZ = Z;
bestLambda = lambda;
bestMp = mp;
bestMs = ms;
end
catch
end
end
fprintf('*********** LEO to GEO result with one
stage **********\n');
if(minTotalMass>0)
fprintf('deltaV=%f\n',deltaV);
fprintf('min total mass=%f kg\n',minTotalMass);
fprintf('m0 = %f kg\n',mL+bestMp+bestMs);
fprintf('mf = %f kg\n',mL+bestMs);
fprintf('best Ve=%f km/sec \n',bestVe);
fprintf('best Isp=%f sec\n',bestVe/g * 1000);
fprintf('best Epsilon=%f \n',bestEpsilon);
fprintf('best
Z =%f \n',bestZ);
fprintf('best lambda=%f \n',bestLambda);
fprintf('best mp =%f \n',bestMp);
fprintf('best ms =%f \n',bestMs);
else
fprintf('Failed to find any one stage that will meet deltaV with given
Isp\n');
fprintf('Please increase number of stages of increase Isp or reduce
payload\n');
end
%try 2 stages
minTotalMass
= Inf;
bestVe = [];
bestEpsilon = [];
bestZ =
[];
bestLambda =
[];
bestMp =
[];
bestMs =
[];
Isp=[295.5
289.1];
Ve=zeros(length(Isp),1);
for(i=1:length(Isp))
Ve(i)=Isp(i)*g/1000; % in
km/sec
end
firstStageVe=Ve(1);
secondStageVe=Ve(2);
for(j=1:length(epsilon))
firstStageEps=epsilon(j);
for(k=1:length(epsilon))
secondStageEps=epsilon(k);
try
lagrange =
nma_rocket_getLagrangeMultiplier(...
deltaV,[firstStageVe secondStageVe],[firstStageEps secondStageEps]);
[Z,mp,ms,lambda]=nma_rocket_mutliStageSolutionLagrange(...
lagrange,[firstStageVe secondStageVe],[firstStageEps
secondStageEps],mL);
totalMass=sum(mp)+sum(ms)+mL;
if( totalMass <= minTotalMass)
minTotalMass = totalMass;
bestVe(1) = firstStageVe;
bestVe(2) = secondStageVe;
bestEpsilon(1) = firstStageEps;
bestEpsilon(2) = secondStageEps;
bestZ = Z;
bestLambda = lambda;
bestMp = mp;
bestMs = ms;
end
catch
end
end
end
fprintf('*********** LEO to GEO with 2 stages
**********\n');
if(minTotalMass>0)
fprintf('deltaV=%f\n',deltaV);
fprintf('min total mass=%f kg\n',minTotalMass);
fprintf('m0 first stage= %f
kg\n',mL+bestMp(1)+bestMp(2)+bestMs(1)+bestMs(2));
fprintf('mf first stage= %f
kg\n',mL+bestMp(2)+bestMs(1)+bestMs(2));
fprintf('m0 second stage= %f kg\n',mL+bestMp(2)+bestMs(2));
fprintf('mf second stage= %f kg\n',mL+bestMs(2));
fprintf('best Ve first Stage=%f km/sec \n',bestVe(1));
fprintf('best Ve second Stage=%f km/sec \n',bestVe(2));
fprintf('best Isp first stage=%f sec\n',bestVe(1)/g * 1000);
fprintf('best Isp second stage=%f sec\n',bestVe(2)/g * 1000);
fprintf('best Epsilon first stage=%f \n',bestEpsilon(1));
fprintf('best Epsilon second stage=%f \n',bestEpsilon(2));
fprintf('best Z first stage=%f \n',bestZ(1));
fprintf('best Z second stage=%f \n',bestZ(2));
fprintf('best
lambda first stage=%f \n',bestLambda(1));
fprintf('best lambda second stage=%f \n',bestLambda(2));
fprintf('best mp first stage =%f \n',bestMp(1));
fprintf('best mp second stage =%f \n',bestMp(2));
fprintf('best ms first stage =%f \n',bestMs(1));
fprintf('best ms second stage =%f \n',bestMs(2));
else
fprintf('Failed to find any one stage that will meet deltaV with given
Isp\n');
fprintf('Please increase number of stages of increase Isp or reduce
payload\n');
end
secondStageM0= minTotalMass;
%try 3 stages
minTotalMass
= Inf;
bestVe = [];
bestEpsilon = [];
bestZ =
[];
bestLambda =
[];
bestMp =
[];
bestMs =
[];
Isp=[295.5 289.1
289.1];
Ve=zeros(length(Isp),1);
for(i=1:length(Isp))
Ve(i)=Isp(i)*g/1000; % in km/sec
end
firstStageVe=Ve(1);
secondStageVe=Ve(2);
thirdStageVe=Ve(3);
for(j=1:length(epsilon))
firstStageEps=epsilon(j);
for(i=1:length(epsilon))
secondStageEps=epsilon(i);
for(k=1:length(epsilon))
thirdStageEps=epsilon(k);
try
lagrange = nma_rocket_getLagrangeMultiplier(...
deltaV,[firstStageVe secondStageVe thirdStageVe],...
[firstStageEps secondStageEps thirdStageEps]);
[Z,mp,ms,lambda]=nma_rocket_mutliStageSolutionLagrange(...
lagrange,[firstStageVe secondStageVe thirdStageVe],...
[firstStageEps secondStageEps thirdStageEps],mL);
totalMass=sum(mp)+sum(ms)+mL;
if( totalMass <= minTotalMass)
minTotalMass = totalMass;
bestVe(1) = firstStageVe;
bestVe(2) = secondStageVe;
bestVe(3) = thirdStageVe;
bestEpsilon(1) = firstStageEps;
bestEpsilon(2) = secondStageEps;
bestEpsilon(3) = thirdStageEps;
bestZ = Z;
bestLambda = lambda;
bestMp = mp;
bestMs = ms;
end
catch
end
end
end
end
fprintf('*********** LEO to GEO with 3 stages
**********\n');
if(minTotalMass>0)
fprintf('deltaV=%f\n',deltaV);
fprintf('min total mass=%f kg\n',minTotalMass);
fprintf('m0 first stage= %f kg\n',mL+bestMp(1)+bestMp(2)+bestMp(3)+...
bestMs(1)+bestMs(2)+bestMs(3));
fprintf('mf first stage= %f
kg\n',mL+bestMp(3)+bestMp(2)+bestMs(1)+bestMs(2)+bestMs(3));
fprintf('m0 second stage= %f
kg\n',mL+bestMp(2)+bestMp(3)+bestMs(2)+bestMs(3));
fprintf('mf second stage= %f
kg\n',mL+bestMs(2)+bestMs(3)+bestMp(3));
fprintf('m0 third stage= %f kg\n',mL+bestMp(3)+bestMs(3));
fprintf('mf third stage= %f kg\n',mL+bestMs(3));
fprintf('best Ve first Stage=%f km/sec \n',bestVe(1));
fprintf('best Ve second Stage=%f km/sec \n',bestVe(2));
fprintf('best Ve third Stage=%f km/sec \n',bestVe(3));
fprintf('best Isp first stage=%f sec\n',bestVe(1)/g * 1000);
fprintf('best Isp second stage=%f sec\n',bestVe(2)/g * 1000);
fprintf('best Isp third stage=%f sec\n',bestVe(3)/g * 1000);
fprintf('best Epsilon first stage=%f \n',bestEpsilon(1));
fprintf('best Epsilon second stage=%f \n',bestEpsilon(2));
fprintf('best Epsilon third stage=%f \n',bestEpsilon(3));
fprintf('best Z first stage=%f \n',bestZ(1));
fprintf('best Z second stage=%f \n',bestZ(2));
fprintf('best Z third stage=%f \n',bestZ(3));
fprintf('best lambda first stage=%f \n',bestLambda(1));
fprintf('best lambda second stage=%f
\n',bestLambda(2));
fprintf('best lambda third stage=%f \n',bestLambda(3));
fprintf('best mp first stage =%f \n',bestMp(1));
fprintf('best mp second stage =%f \n',bestMp(2));
fprintf('best mp third stage =%f \n',bestMp(3));
fprintf('best ms first stage =%f \n',bestMs(1));
fprintf('best ms second stage =%f \n',bestMs(2));
fprintf('best ms third stage =%f \n',bestMs(3));
else
fprintf('Failed to find any one stage that will meet deltaV with given
Isp\n');
fprintf('Please increase number of stages of increase Isp or reduce
payload\n');
end
%do this below becuase I want to only use 2 stages
for LEO to GEO, so I
%want to carry the load below.
mL=secondStageM0;
% Now do the earth
to LEO
Isp=[301];
Ve=zeros(length(Isp),1);
for(i=1:length(Isp))
Ve(i)=Isp(i)*g/1000; % in
km/sec
end
firstStageVe=Ve(1);
minTotalMass
= Inf;
bestVe = [];
bestEpsilon = [];
bestZ =
[];
bestLambda =
[];
bestMp = [];
bestMs =
[];
%one stage try
SOLVED=FALSE;
deltaV=9.412; % km/sec, from design project I. last
step
for(j=1:length(epsilon))
try
lagrange =
nma_rocket_getLagrangeMultiplier(deltaV,firstStageVe,epsilon(j));
[Z,mp,ms,lambda]=nma_rocket_mutliStageSolutionLagrange(lagrange,firstStageVe,epsilon(j),mL);
SOLVED=TRUE;
totalMass=sum(mp)+sum(ms)+mL;
if(
totalMass <= minTotalMass)
%fprintf('totalMass=%f, j=%d, i=%d\n',totalMass,j,i);
minTotalMass = totalMass;
bestVe = Ve(i);
bestEpsilon = epsilon(j);
bestZ = Z;
bestLambda = lambda;
bestMp = mp;
bestMs = ms;
end
catch
end
end
if(~SOLVED)
fprintf('********Failed to solve earth to LEO with one stage\n');
else
fprintf('*********** earth to LEO result with one stage **********\n');
fprintf('deltaV=%f\n',deltaV);
fprintf('min total mass=%f kg\n',minTotalMass);
fprintf('m0 = %f kg\n',mL+bestMp+bestMs);
fprintf('mf = %f kg\n',mL+bestMs);
fprintf('best Ve=%f km/sec \n',bestVe);
fprintf('best Isp=%f sec\n',bestVe/g * 1000);
fprintf('best Epsilon=%f \n',bestEpsilon);
fprintf('best Z =%f \n',bestZ);
fprintf('best
lambda=%f \n',bestLambda);
fprintf('best mp =%f \n',bestMp);
fprintf('best ms =%f \n',bestMs);
end
%try 2 stages
minTotalMass
= Inf;
bestVe = [];
bestEpsilon = [];
bestZ =
[];
bestLambda =
[];
bestMp =
[];
bestMs =
[];
Isp=[301
316];
Ve=zeros(length(Isp),1);
for(i=1:length(Isp))
Ve(i)=Isp(i)*g/1000; % in
km/sec
end
firstStageVe=Ve(1);
secondStageVe=Ve(2);
for(j=1:length(epsilon))
firstStageEps=epsilon(j);
for(i=1:length(epsilon))
secondStageEps=epsilon(i);
try
lagrange = nma_rocket_getLagrangeMultiplier(...
deltaV,[firstStageVe secondStageVe],[firstStageEps secondStageEps]);
[Z,mp,ms,lambda]=nma_rocket_mutliStageSolutionLagrange(...
lagrange,[firstStageVe secondStageVe],[firstStageEps
secondStageEps],mL);
totalMass=sum(mp)+sum(ms)+mL;
if( totalMass <= minTotalMass)
minTotalMass = totalMass;
bestVe(1) = firstStageVe;
bestVe(2) = secondStageVe;
bestEpsilon(1) = firstStageEps;
bestEpsilon(2) = secondStageEps;
bestZ = Z;
bestLambda = lambda;
bestMp = mp;
bestMs = ms;
end
catch
end
end
end
fprintf('*********** earth to LEO with 2 stages
**********\n');
if(minTotalMass>0)
fprintf('deltaV=%f\n',deltaV);
fprintf('min total mass=%f kg\n',minTotalMass);
fprintf('m0 first stage= %f
kg\n',mL+bestMp(1)+bestMp(2)+bestMs(1)+bestMs(2));
fprintf('mf first stage= %f
kg\n',mL+bestMp(2)+bestMs(1)+bestMs(2));
fprintf('m0 second stage= %f kg\n',mL+bestMp(2)+bestMs(2));
fprintf('mf second stage= %f kg\n',mL+bestMs(2));
fprintf('best Ve first Stage=%f km/sec \n',bestVe(1));
fprintf('best Ve second Stage=%f km/sec \n',bestVe(2));
fprintf('best Isp first stage=%f sec\n',bestVe(1)/g * 1000);
fprintf('best Isp second stage=%f
sec\n',bestVe(2)/g * 1000);
fprintf('best Epsilon first stage=%f \n',bestEpsilon(1));
fprintf('best Epsilon second stage=%f \n',bestEpsilon(2));
fprintf('best Z first stage=%f \n',bestZ(1));
fprintf('best
Z second stage=%f \n',bestZ(2));
fprintf('best lambda first stage=%f \n',bestLambda(1));
fprintf('best lambda second stage=%f \n',bestLambda(2));
fprintf('best mp first stage =%f \n',bestMp(1));
fprintf('best mp second stage =%f \n',bestMp(2));
fprintf('best ms first stage =%f \n',bestMs(1));
fprintf('best ms second stage =%f \n',bestMs(2));
else
fprintf('Failed to find any one stage that will meet deltaV with given
Isp\n');
fprintf('Please increase number of stages of increase Isp or reduce
payload\n');
end
%try 3 stages
minTotalMass
= Inf;
bestVe = [];
bestEpsilon = [];
bestZ =
[];
bestLambda =
[];
bestMp =
[];
bestMs =
[];
Isp=[301 316
316];
Ve=zeros(length(Isp),1);
for(i=1:length(Isp))
Ve(i)=Isp(i)*g/1000; % in
km/sec
end
firstStageVe=Ve(1);
secondStageVe=Ve(2);
thirdStageVe=Ve(3);
SOLVED=FALSE;
for(j=1:length(epsilon))
firstStageEps=epsilon(j);
for(i=1:length(epsilon))
secondStageEps=epsilon(i);
for(k=1:length(epsilon))
thirdStageEps=epsilon(k);
try
lagrange = nma_rocket_getLagrangeMultiplier(...
deltaV,[firstStageVe secondStageVe thirdStageVe],...
[firstStageEps secondStageEps
thirdStageEps]);
[Z,mp,ms,lambda]=nma_rocket_mutliStageSolutionLagrange(...
lagrange,[firstStageVe secondStageVe thirdStageVe],...
[firstStageEps secondStageEps thirdStageEps],mL);
SOLVED=TRUE;
totalMass=sum(mp)+sum(ms)+mL;
if( totalMass <= minTotalMass)
minTotalMass = totalMass;
bestVe(1) = firstStageVe;
bestVe(2) = secondStageVe;
bestVe(3) = thirdStageVe;
bestEpsilon(1) = firstStageEps;
bestEpsilon(2) = secondStageEps;
bestEpsilon(3) = thirdStageEps;
bestZ = Z;
bestLambda = lambda;
bestMp = mp;
bestMs = ms;
end
catch
end
end
end
end
if(~SOLVED)
error('Failed to solve earth to LEO with 3 stages');
end
fprintf('*********** earth to LEO with 3 stages
**********\n');
if(minTotalMass>0)
fprintf('deltaV=%f\n',deltaV);
fprintf('min total mass=%f kg\n',minTotalMass);
fprintf('m0 first stage= %f kg\n',mL+bestMp(1)+bestMp(2)+bestMp(3)+...
bestMs(1)+bestMs(2)+bestMs(3));
fprintf('mf first stage= %f
kg\n',mL+bestMp(3)+bestMp(2)+bestMs(1)+bestMs(2)+bestMs(3));
fprintf('m0 second stage= %f
kg\n',mL+bestMp(2)+bestMp(3)+bestMs(2)+bestMs(3));
fprintf('mf second stage= %f
kg\n',mL+bestMs(2)+bestMs(3)+bestMp(3));
fprintf('m0 third stage= %f kg\n',mL+bestMp(3)+bestMs(3));
fprintf('mf third stage= %f
kg\n',mL+bestMs(3));
fprintf('best Ve first Stage=%f km/sec \n',bestVe(1));
fprintf('best Ve second Stage=%f km/sec \n',bestVe(2));
fprintf('best Ve third Stage=%f km/sec \n',bestVe(3));
fprintf('best
Isp first stage=%f sec\n',bestVe(1)/g * 1000);
fprintf('best Isp second stage=%f sec\n',bestVe(2)/g * 1000);
fprintf('best Isp third stage=%f sec\n',bestVe(3)/g * 1000);
fprintf('best Epsilon first stage=%f \n',bestEpsilon(1));
fprintf('best Epsilon second stage=%f \n',bestEpsilon(2));
fprintf('best Epsilon third stage=%f \n',bestEpsilon(3));
fprintf('best Z first stage=%f \n',bestZ(1));
fprintf('best Z second stage=%f \n',bestZ(2));
fprintf('best
Z third stage=%f \n',bestZ(3));
fprintf('best lambda first stage=%f \n',bestLambda(1));
fprintf('best lambda second stage=%f \n',bestLambda(2));
fprintf('best lambda third stage=%f \n',bestLambda(3));
fprintf('best mp first stage =%f \n',bestMp(1));
fprintf('best mp second stage =%f \n',bestMp(2));
fprintf('best mp third stage =%f \n',bestMp(3));
fprintf('best ms first stage =%f \n',bestMs(1));
fprintf('best ms second stage =%f \n',bestMs(2));
fprintf('best
ms third stage =%f \n',bestMs(3));
else
fprintf('Failed to find any one stage that will meet deltaV with given
Isp\n');
fprintf('Please increase number of stages of increase Isp or reduce
payload\n');
end