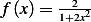 This function is an even function:
This function is an even function:
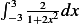
Answer
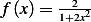 This function is an even function:
This function is an even function:
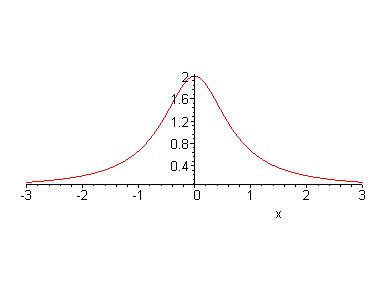
f(x)
hence
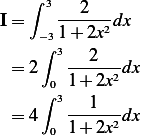
First transform the integral to be inside the limits of 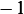 to
to 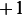 . Let
. Let 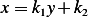
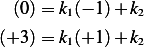
Solve for 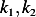 . Adding the above 2 equations gives
. Adding the above 2 equations gives 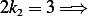 _____
_____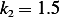
Hence, 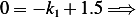 _____
_____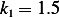
hence the transformation is_______________________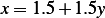 and ____________________
and ____________________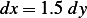
Using the above transformation, the integral becomes
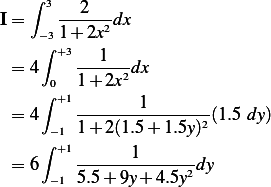
Hence 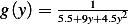
2 points Gauss
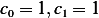 ,
,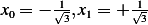
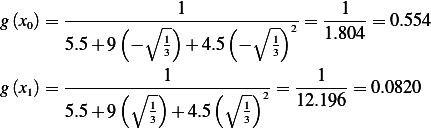
Hence
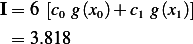
3 points Gauss
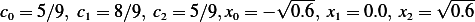
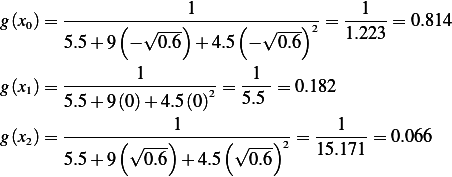
Hence
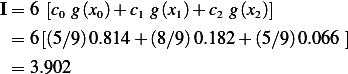
4 points Gauss
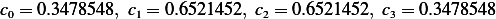
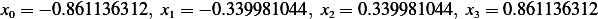
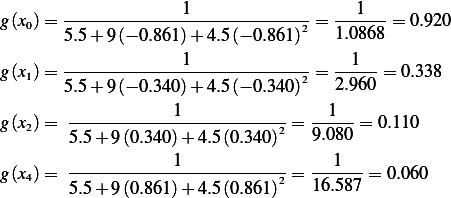
so
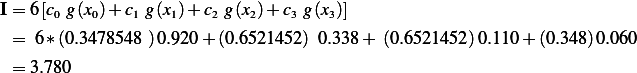
5 points Gauss
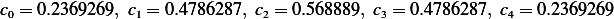
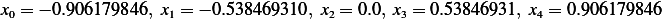

Hence,
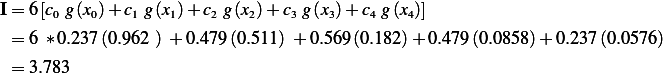
6 points Gauss
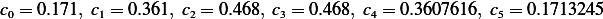
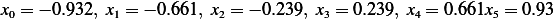

Hence
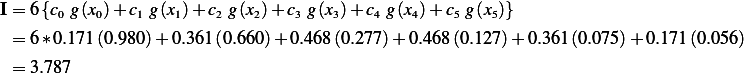
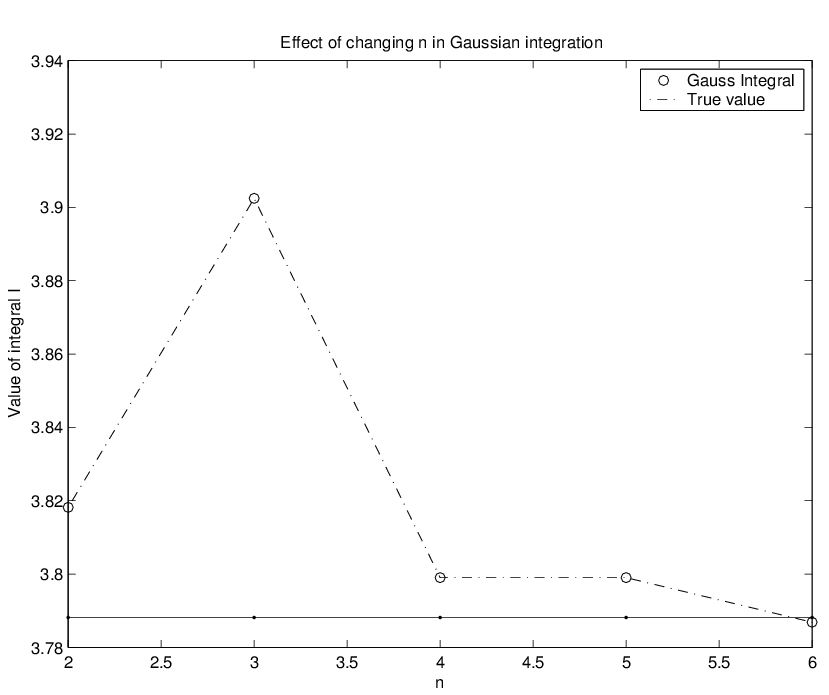
summary: This table shows the relative error normalized to the true value for value of number of points n, starting with n=2 up to n=6. Analytically,
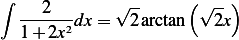
hence
![∫ 3 2 [√ -- (√ -- ) √ -- ( √-- ) ]
Ianalytical = 2 -----2dx = 2 2arctan 2(3) − 2arctan 2 (0 ) = 2[1.894]= 3.788
0 1+ 2x](pr38x.png)
So 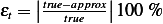
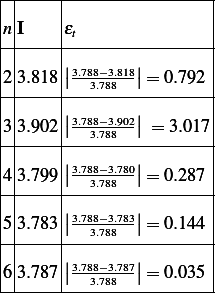
As number of points increases, the acurracy increases.
observation: I am able to find why the n=3 case seems to have some abnormality. 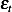 should decrease
as n increases, but for n=3 it did not. Checked the calculations but not able to see if I did some arithmitic
error.
should decrease
as n increases, but for n=3 it did not. Checked the calculations but not able to see if I did some arithmitic
error.