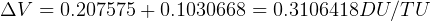 is given as
is given as 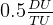 , and
, and 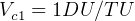 , then service orbit must be the larger orbit (outside
orbit), since the smaller the distance from the attracting body the larger the velosity of the orbiting
body).
, then service orbit must be the larger orbit (outside
orbit), since the smaller the distance from the attracting body the larger the velosity of the orbiting
body).
Analysis:
Since 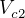 is given as
is given as 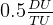 , and
, and 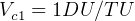 , then service orbit must be the larger orbit (outside
orbit), since the smaller the distance from the attracting body the larger the velosity of the orbiting
body).
, then service orbit must be the larger orbit (outside
orbit), since the smaller the distance from the attracting body the larger the velosity of the orbiting
body).
First find 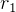 and
and 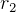
Since 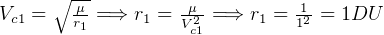
Similarly 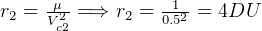
From geometry, for the transfer orbit, 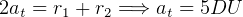
But 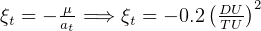
Now, velocity in the transfer orbit is given by 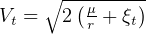 hence at point 1,
hence at point 1, 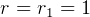 DU, so we get
DU, so we get
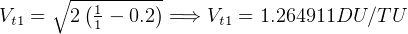
Similarly, 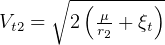 hence at point 2,
hence at point 2, 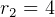 DU, so we get
DU, so we get 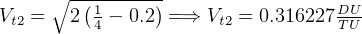
So, 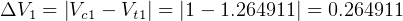 DU/TU
DU/TU
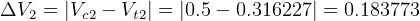 DU/TU
DU/TU
hence, minumum 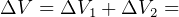 ____________________________
____________________________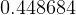 DU/TU
DU/TU
Compute the minimum 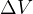 required to transfer between 2 coplaner elliptical orbits which have their major
axes aligned. The parameters are:
required to transfer between 2 coplaner elliptical orbits which have their major
axes aligned. The parameters are:
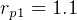 DU.
DU. 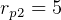 DU
DU 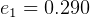 DU.
DU. 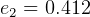 DU
DU
Assume both preigrees lie on the same side of the earth.
Assumptions:
Method: First find 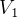 and
and 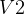 , the velositites for ellips 1 at its perigree and for ellips 2 at its
apegee.
, the velositites for ellips 1 at its perigree and for ellips 2 at its
apegee.
Next find 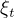 , the energy for the transfer orbit. From this, find
, the energy for the transfer orbit. From this, find 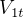 and
and 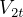 , the velosities in the transfer
orbit at point 1 and point 2 respectively.
, the velosities in the transfer
orbit at point 1 and point 2 respectively.
Finally, final 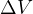 follows as from the sum of the
follows as from the sum of the 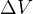 at point 1 and point 2.
at point 1 and point 2.
This is the minumum, since the transfer orbit is a Homann orbit.
Analysis:

since 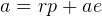 from ellips geometry.
from ellips geometry.
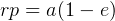
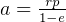
For ellips 1:
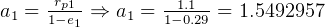 DU.
DU.
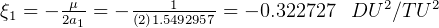
But 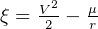 , hence, since
, hence, since 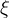 is constant over the orbit, we can use this relationship to solve for
is constant over the orbit, we can use this relationship to solve for 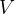 for
different
for
different  .
.
At point 1, for first ellips, 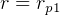 , hence
, hence
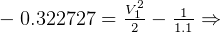 _______________________
_______________________
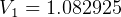 DU/TU.
DU/TU.
For ellips 2:
Here we want to find the velosity 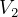 , the velosity at the apegee for ellips 2. So, need to find
, the velosity at the apegee for ellips 2. So, need to find 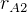 for ellips
2.
for ellips
2.
Since 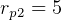 DU, and
DU, and 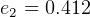 , we get
, we get
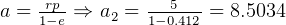 DU.
DU.
Hence, since 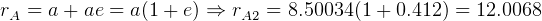 DU.
DU.
Now find 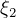 the energy for ellips 2
the energy for ellips 2
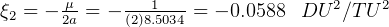
but 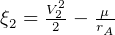 then
then
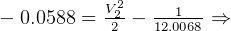 ________________________
________________________
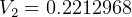 DU/TU
DU/TU
For the transfer orbit:
From geometry, 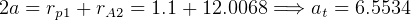 DU
DU
so 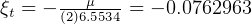
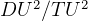
So, 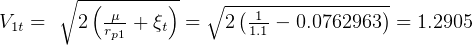 DU/TU
DU/TU
So, 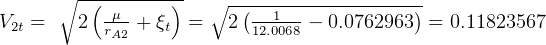 DU/TU
DU/TU
so 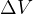 at point 1
at point 1 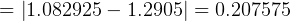 DU/TU
DU/TU
so 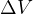 at point 2
at point 2  DU/TU
DU/TU
hence minumum