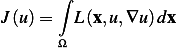 over all
over all 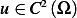 with
with
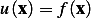 at boundary
at boundary 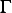 where
where 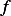 is a given function.
is a given function.  is bounded and well behaved in
is bounded and well behaved in
problem:
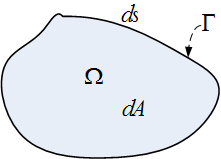
Consider the problem of minimizing the functional 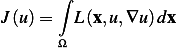 over all
over all 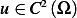 with
with
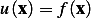 at boundary
at boundary 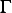 where
where 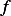 is a given function.
is a given function.  is bounded and well behaved in
is bounded and well behaved in
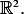
(a) Show that the first variation is (Where 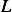 below is meant to be
below is meant to be 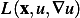 ) where
) where  is the vector
is the vector

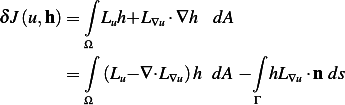
Where 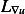 is the vector
is the vector 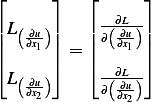 and
and 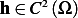 with
with 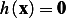 at the boundary
at the boundary
(b)Show that the necessary condition for  to minimize
to minimize 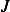 is that
is that  must satisfy the Euler equation
must satisfy the Euler equation
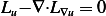 ,
, 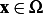
(c)If  is not fixed on the boundary
is not fixed on the boundary 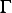 find the natural boundary conditions.
find the natural boundary conditions.
Answer
(a)
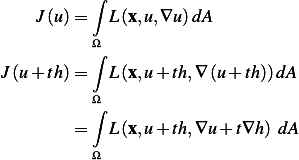
Hence
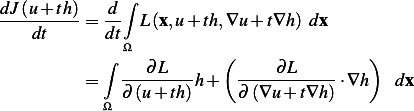
But  , hence at
, hence at 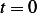 the above becomes
the above becomes
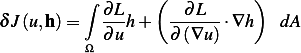 | (1) |
But 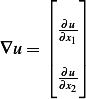 , hence
, hence 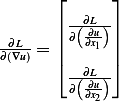 , and
, and 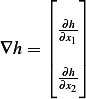 , therefore
, therefore
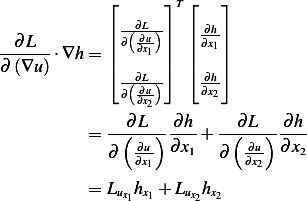
Hence (1) becomes
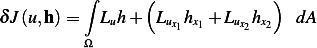 | (2) |
Now
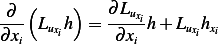
Hence
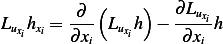
Hence substitute the above in (2) for 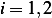 we obtain
we obtain
Now using Green theorem, where
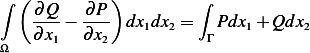
Let 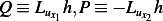 , hence Green theorem becomes
, hence Green theorem becomes
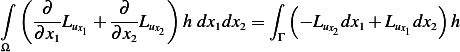
Substitute the above into second term in (3) we obtain (noting that 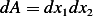 since we are in
since we are in
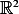 )
)
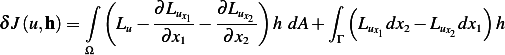 | (4) |
But the second integral above can be rewritten as (by dividing and multiplying by 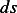 )
)
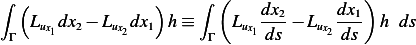
Hence (4) becomes
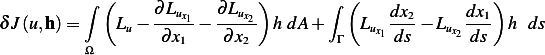 | (5) |
Now Tangent vector at the boundary at point 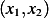 is given by vector
is given by vector 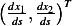 , hence the normal is
, hence the normal is
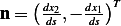 (since if we take dot product of these 2 vectors we get zero). Now we can rewrite the
integrand in the second integral in (5) in terms of this normal vector since
(since if we take dot product of these 2 vectors we get zero). Now we can rewrite the
integrand in the second integral in (5) in terms of this normal vector since
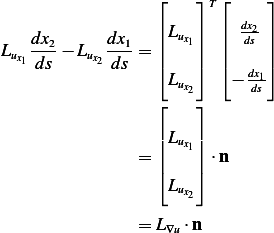
Substitute the above into the second term of (5) we obtain

Final note on the sign before the second integral above. The book shows it as  . I think this is because
the normal should be pointing outside? Hence if we make out normal the negative of the normal
used here (which I think points inwards), we obtain the result we are asked to show for part (a).
(notice, the book has a mistake/typo, it says
. I think this is because
the normal should be pointing outside? Hence if we make out normal the negative of the normal
used here (which I think points inwards), we obtain the result we are asked to show for part (a).
(notice, the book has a mistake/typo, it says 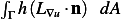 instead of
instead of 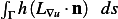 , i.e. the
integration is over a line segment, not over a differential area (since obviously this is contour
integration).
, i.e. the
integration is over a line segment, not over a differential area (since obviously this is contour
integration).
part (b)
Necessary condition for minimum is that 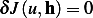 ,. ie.
,. ie.
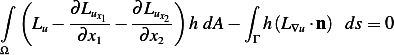
Now consider the second integral in the above. Since 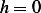 on
on 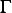 , hence we are left to show
that
, hence we are left to show
that
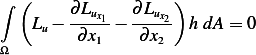
But 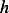 is arbitrary function, hence by lemma 3.13 again, we argue that for the above to be zero,
then
is arbitrary function, hence by lemma 3.13 again, we argue that for the above to be zero,
then
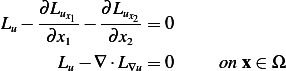
Which is Euler-Lagrange equation.
Part (c)
Here we have free boundary conditions. Hence we can not take 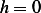 everywhere on
everywhere on  . Starting with the
first variation
. Starting with the
first variation
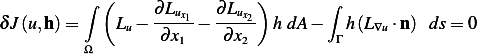
Since 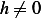 on
on 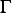 then by lemma 3.13 we can argue that
then by lemma 3.13 we can argue that 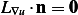 on
on 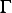
Hence on 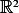 , this means
, this means 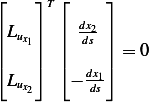 , i.e.
, i.e.
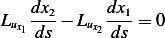
Now we need to know the shape of the boundary to evaluate the above at each point. For example, for a
circle, 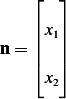 and the above become
and the above become
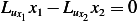
And the above equation needs to be satisfied at each point on the boundary after discretization.