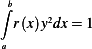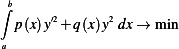
problem:
Write down the equations that determine the solution of the isoperimetric problem
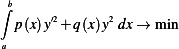
Subject to
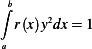
where 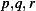 are given functions and
are given functions and 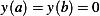 .
.
Answer
Since 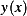 is fixed at each end, this is not a natural boundary problem. Therefore one can use the auxiliary lagrangian approach,
where we write the auxiliary Lagrangian
is fixed at each end, this is not a natural boundary problem. Therefore one can use the auxiliary lagrangian approach,
where we write the auxiliary Lagrangian 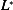 as
as
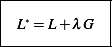
Where 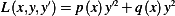 , and
, and 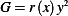 and
and 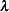 is the Lagrangian multiplier. Hence
is the Lagrangian multiplier. Hence
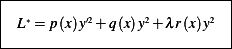
Hence now we write the solution as the Euler-Lagrange equation, but we use 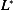 instead of
instead of 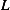
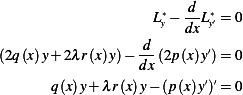
Therefore the differential equation is
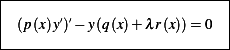
This is a sturm-Liouville eigenvalue problem. The solution 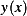 from the above will contain 3 constants. 2 will be found from
boundary conditions, and the third, which is
from the above will contain 3 constants. 2 will be found from
boundary conditions, and the third, which is 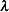 is found from plugging in the solution
is found from plugging in the solution 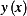 into the constraint given:
into the constraint given: