HOME
HW 7 Mathematics 503, Mathematical Modeling, CSUF , July 9, 2007
Nasser M. Abbasi
June 15, 2014
Contents
1 Problem 1
problem:
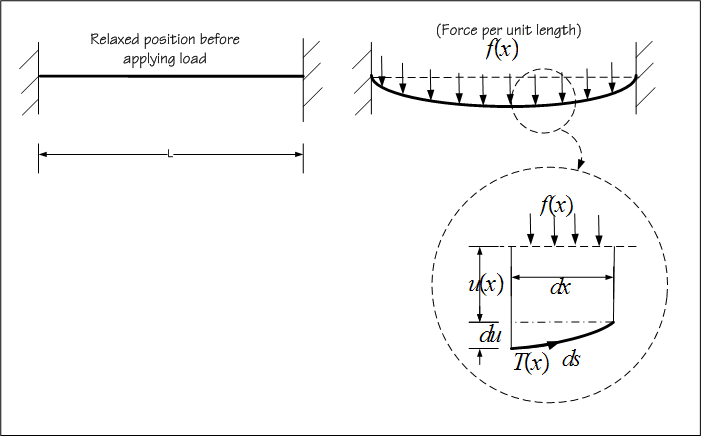
Consider a taut string that is held fixed at 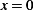 and
and 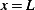 . Load on string is
. Load on string is 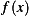 which is force per unit length. Tension is
which is force per unit length. Tension is
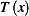 . Suppose the deflection of string is
. Suppose the deflection of string is 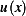 is continuously differentiable function. (a) Argue that when the string is in
equilibrium and the deflection is small, the potential energy is
is continuously differentiable function. (a) Argue that when the string is in
equilibrium and the deflection is small, the potential energy is
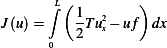
(b) Use variational argument to characterization of weak solution.
(c) Verify that a weak solution minimizes this energy functional 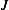
Solution:
(a) The potential energy of the string is made up of 2 parts. The first is due to work done by 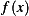 is moving the string lower by a
distance
is moving the string lower by a
distance 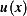 from its relaxed position, and the second due to the work done by
from its relaxed position, and the second due to the work done by 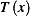 in stretching the string from length of
in stretching the string from length of 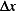 to
length of
to
length of 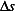
Now we calculate the potential energy. Due to 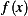 doing work over distance of
doing work over distance of 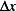 is
is

due to Tension 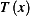 doing work over distance
doing work over distance 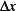 is
is
But for small deflection 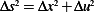 , hence
, hence 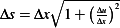 hence the above becomes
hence the above becomes
For small 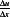 ,
, 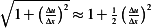 , so the above becomes
, so the above becomes
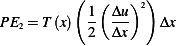
Hence total potential energy per unit length is
Hence total 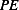 is found by integrating the above over the total length of the sting
is found by integrating the above over the total length of the sting
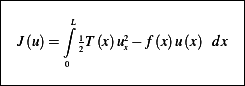
(b) Assume the string is in equilibrium position. The deflection 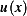 at equilibrium will be such that it renders the
at equilibrium will be such that it renders the 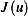 minimum. (This is a basic principle in physics, in which physical systems when in equilibrium will be in such configuration such
that the total potential energy needed to achieve this configuration is minimal). Hence this is a minimization problem
of the above function. Let the set of feasible solution
minimum. (This is a basic principle in physics, in which physical systems when in equilibrium will be in such configuration such
that the total potential energy needed to achieve this configuration is minimal). Hence this is a minimization problem
of the above function. Let the set of feasible solution 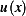 be
be ![A ={u∈ C1[0,L],s.t.u(0)= 0,u(L)= 0}](ma32x.png) and let the
set of feasible directions
and let the
set of feasible directions ![Ad ={h∈ C1[0,L],s.t.h(0)=0,h(L)=0}](ma33x.png) , then a variation of
, then a variation of 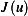 in the direction of
in the direction of 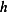 is
is
Hence
From the above we see that directional derivative of 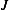 in the direction of
in the direction of 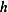 is the linear term which is
is the linear term which is
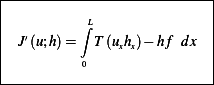
The solution 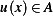 such that
such that 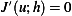 for all
for all 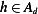 is called the weak solution. Notice that a weak solution requires only
that
is called the weak solution. Notice that a weak solution requires only
that  be once differentiable, i.e.
be once differentiable, i.e. ![1
u∈ C [0,L]](ma45x.png) .
.
(c)A weak solution minimizes 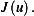 Looking at (1) above, we see that the second term is positive. Hence if
Looking at (1) above, we see that the second term is positive. Hence if 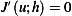 , which
is the third term in (1), then this implies that a small variation from
, which
is the third term in (1), then this implies that a small variation from 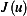 in the direction of
in the direction of 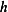 would result in larger value of
would result in larger value of 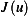 ,
Hence
,
Hence 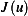 is at a minimum.
is at a minimum.
2 Problem 2
Problem: For the membrane problem, show that a classical solution is a weak solution.
Answer:
From notes, we found that classical solution implied that 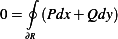 , but
, but 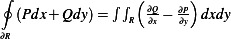 where
where
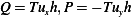
Hence
But since a classical solution is assumed, hence
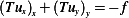
Where the above is the classical solution as derived in the notes. But the above is just 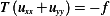 , hence if replace the first
term in the intrange in (1) by this solution, we have
, hence if replace the first
term in the intrange in (1) by this solution, we have
But this is the weak solution 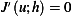 as shown in the top of page 2 in the membrane notes. Hence a classical solution implied
a weak solution.
as shown in the top of page 2 in the membrane notes. Hence a classical solution implied
a weak solution.
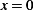 and
and 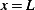 . Load on string is
. Load on string is 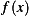 which is force per unit length. Tension is
which is force per unit length. Tension is
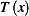 . Suppose the deflection of string is
. Suppose the deflection of string is 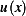 is continuously differentiable function. (a) Argue that when the string is in
equilibrium and the deflection is small, the potential energy is
is continuously differentiable function. (a) Argue that when the string is in
equilibrium and the deflection is small, the potential energy is
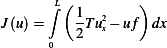
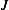
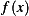 is moving the string lower by a
distance
is moving the string lower by a
distance 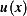 from its relaxed position, and the second due to the work done by
from its relaxed position, and the second due to the work done by 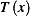 in stretching the string from length of
in stretching the string from length of 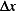 to
length of
to
length of 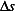
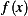 doing work over distance of
doing work over distance of 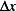 is
is

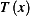 doing work over distance
doing work over distance 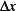 is
is
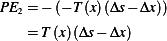
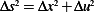 , hence
, hence 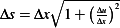 hence the above becomes
hence the above becomes
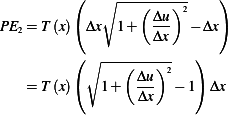
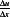 ,
, 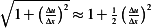 , so the above becomes
, so the above becomes
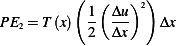
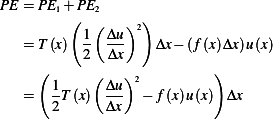
 is found by integrating the above over the total length of the sting
is found by integrating the above over the total length of the sting
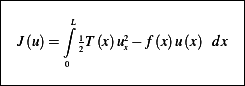
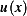 at equilibrium will be such that it renders the
at equilibrium will be such that it renders the 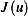 minimum. (This is a basic principle in physics, in which physical systems when in equilibrium will be in such configuration such
that the total potential energy needed to achieve this configuration is minimal). Hence this is a minimization problem
of the above function. Let the set of feasible solution
minimum. (This is a basic principle in physics, in which physical systems when in equilibrium will be in such configuration such
that the total potential energy needed to achieve this configuration is minimal). Hence this is a minimization problem
of the above function. Let the set of feasible solution 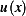 be
be ![A ={u∈ C1[0,L],s.t.u(0)= 0,u(L)= 0}](ma32x.png) and let the
set of feasible directions
and let the
set of feasible directions ![Ad ={h∈ C1[0,L],s.t.h(0)=0,h(L)=0}](ma33x.png) , then a variation of
, then a variation of 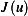 in the direction of
in the direction of 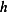 is
is
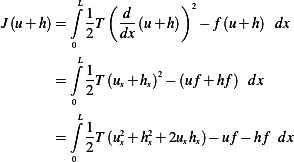
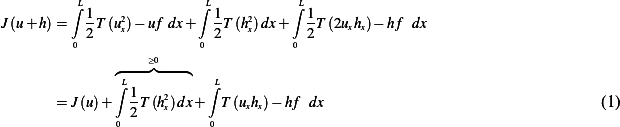
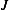 in the direction of
in the direction of 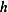 is the linear term which is
is the linear term which is
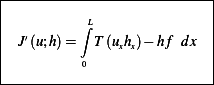
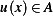 such that
such that 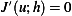 for all
for all 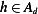 is called the weak solution. Notice that a weak solution requires only
that
is called the weak solution. Notice that a weak solution requires only
that  be once differentiable, i.e.
be once differentiable, i.e. ![1
u∈ C [0,L]](ma45x.png) .
.
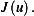 Looking at (1) above, we see that the second term is positive. Hence if
Looking at (1) above, we see that the second term is positive. Hence if 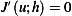 , which
is the third term in (1), then this implies that a small variation from
, which
is the third term in (1), then this implies that a small variation from 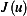 in the direction of
in the direction of 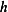 would result in larger value of
would result in larger value of 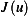 ,
Hence
,
Hence 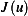 is at a minimum.
is at a minimum.
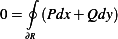 , but
, but 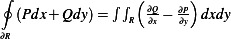 where
where
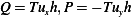
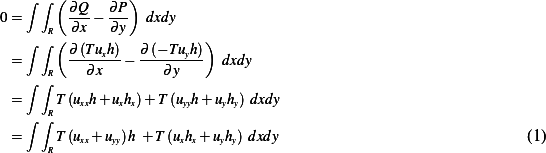
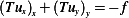
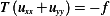 , hence if replace the first
term in the intrange in (1) by this solution, we have
, hence if replace the first
term in the intrange in (1) by this solution, we have

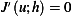 as shown in the top of page 2 in the membrane notes. Hence a classical solution implied
a weak solution.
as shown in the top of page 2 in the membrane notes. Hence a classical solution implied
a weak solution.