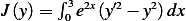
problem: Find extrermals for the following functional:
(b) 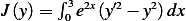
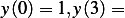 free
free
Solution:
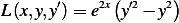
Starting from first principles. First the preliminary standard setup:
Let 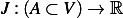 , where
, where 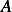 is the set of admissible functions, and
is the set of admissible functions, and ![V :C2 [a,b]](ma7x.png) , hence
, hence
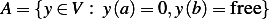
Let 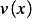 be the set
be the set 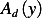 of the permissible directions defined as
of the permissible directions defined as 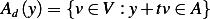 for some
real scalar
for some
real scalar 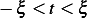
And 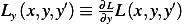 and
and 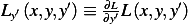
Now we write
Therefor a necessary condition for 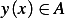 to be a local minimum for the functional
to be a local minimum for the functional 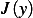 is that
is that
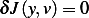 for all
for all 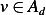 , which means
, which means
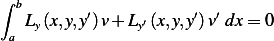
Integrating by parts the second term above results in the general expression for the necessary condition for
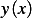 to be a local minimum for
to be a local minimum for 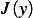 , which is
, which is
![∫ b{ d }
Ly(x,y,y′)− --Ly′(x,y,y′) v dx + [Ly′(x,y,y′)v]ba = 0
a dx](ma23x.png) | (see 3.15 in text) |
Since 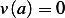 , the second term above simplifies, and the above equation becomes
, the second term above simplifies, and the above equation becomes
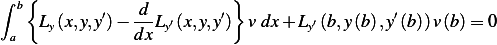 | (1) |
Now we apply the following argument: Out of all functions 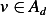 , we can find a set which has the
property such that
, we can find a set which has the
property such that 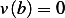 . For these
. For these 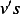 only (1) becomes
only (1) becomes
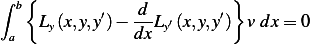
Where now we apply the other standard argument: Since the above is true for every arbitrary  (but
remember now
(but
remember now  is such that
is such that 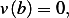 but since there are so many such
but since there are so many such 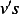 still, then the argument still
holds) , then it must mean that
still, then the argument still
holds) , then it must mean that
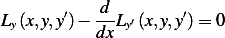 | (2) |
This will generate a second order ODE, which we will solve, with the boundary conditions
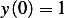
But we need another boundary condition. Then we hold off solving this for one moment. Let us now
consider those functions 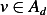 which have the property that
which have the property that 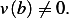 For these
For these  's, and for the second term
in (1) to become zero, we now must have
's, and for the second term
in (1) to become zero, we now must have
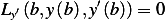 | (3) |
Now from (3) we have 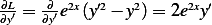 , which means
, which means
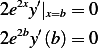
Hence
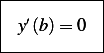
This gives us the second boundary condition we needed to solve (2).
Hence to summarize the problem becomes that of solving for 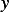 given
given
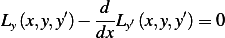
with the boundary conditions 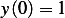 and
and 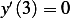
Now (2) can be written as
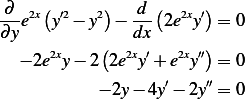
Hence

Assume 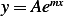 , hence the characteristic equation is
, hence the characteristic equation is 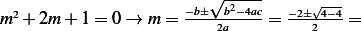
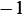
Since we have repeated root, then the solution is
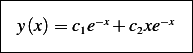
When 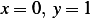 , hence
, hence 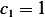
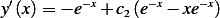
when 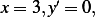 hence
hence 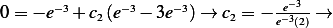
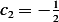
Hence the solution is
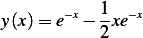
or
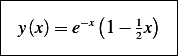
problem: determine the natural boundary condition at 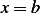 for the variational problem defined by
for the variational problem defined by
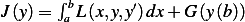 where
where ![2
y ∈ C [a,b],y(a)= y0](ma63x.png) and
and  is a given differentiable function on
is a given differentiable function on
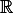
Solution:
Starting from first principles, first the preliminary standard setup.
Let 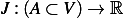 , where
, where 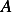 is the set of admissible functions, and
is the set of admissible functions, and ![V :C2 [a,b]](ma68x.png) Hence
Hence
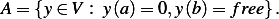 Let
Let 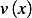 be a set
be a set 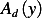 of permissible directions defined as
of permissible directions defined as
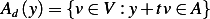 for some real scalar
for some real scalar 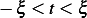 , and Let
, and Let 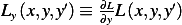 , and
, and
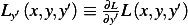
Now we write
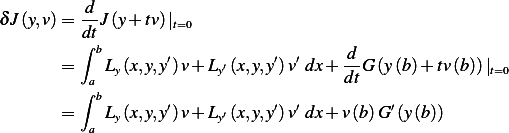
Therefor a necessary condition for 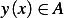 to be a local minimum for
to be a local minimum for 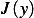 is that
is that 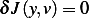 for all
for all
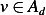 , which means
, which means
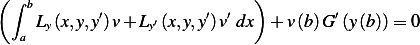
Integrating the second term in the integral above by parts results in the general expression for the necessary
condition for 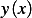 to be a local minimum for
to be a local minimum for 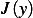 , which is
, which is
![∫ b{ }
Ly(x,y,y′)− d-Ly′(x,y,y′) v dx + [Ly′(x,y,y′)v]b+ v(b)G′(y(b))= 0
a dx a](ma84x.png)
Hence
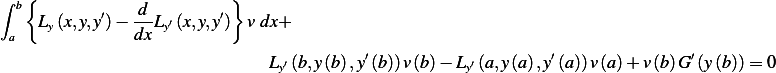 |
Since 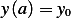 , we must have
, we must have 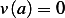 , then the above simplifies to
, then the above simplifies to
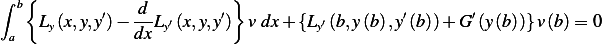 | (1) |
Let us now consider those functions 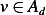 which have the property that
which have the property that 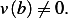 For these
For these  's, for the
second term in (1) to become zero, we now must have
's, for the
second term in (1) to become zero, we now must have
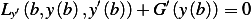
Hence
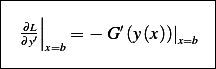
Hence the natural boundary condition on 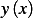 at
at 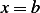 must satisfy the above. (I do not see how can
one go further without being given what
must satisfy the above. (I do not see how can
one go further without being given what  and
and  are.)
are.)