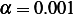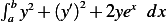
problem: Find extrermals for the following functional:
(b) 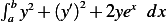
Solution:
Assume first that 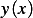 has normal conditions on the boundaries. I.e.
has normal conditions on the boundaries. I.e. 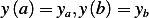
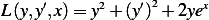
We have the functional
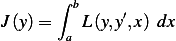
and we seek to find a function 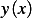 which minimizes this functional.
which minimizes this functional.
Let the vector space from which we can pick 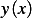 from be
from be
![2
V = C [a,b]](ma9x.png)
And let the set of admissible functions (within 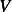 ) (Is this set a subspace?) be defined as
) (Is this set a subspace?) be defined as
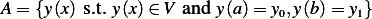
And let the set of admissible directions 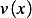 be
be
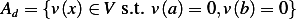
Use the variational method since the Lagrangian contains a quadratic terms.
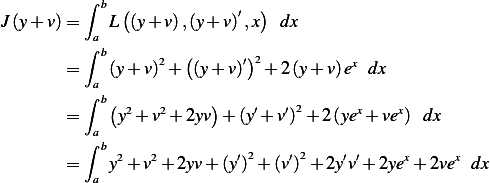
rearrange terms
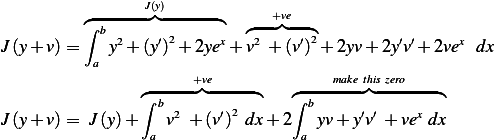
Hence if we can find  which will make the last term above zero, then
which will make the last term above zero, then 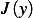 will have been minimized
by this
will have been minimized
by this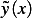
Therefor the problem now becomes of solving for 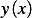 the following integral equation
the following integral equation
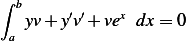 | (1) |
We need to try to convert the above into something like 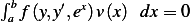 so that we can say that
so that we can say that
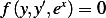 , so this means in (1) we need to do integration by parts on the term
, so this means in (1) we need to do integration by parts on the term 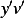 . Hence (1) can be
written as
. Hence (1) can be
written as
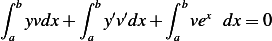
Now since ![∫ u dz = [uz]b− ∫bz du
a a](ma25x.png) , now let
, now let 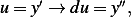 and let
and let 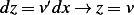 , hence we
have
, hence we
have
![∫ ◜◞0◟|◝ ∫
by′v′dx= [y′v]b− bvy′′ dx
a a a](ma28x.png)
Hence (1) can be written as
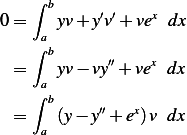
Now we apply the standard argument and say that since 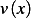 is arbitrary function, and the integral above
is always zero, then it must be that
is arbitrary function, and the integral above
is always zero, then it must be that
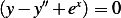
or
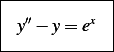
This is a linear second order ODE with constant coefficients with a forcing function. The
homogeneous ODE will have 2 independent solutions, say 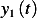 and
and 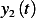 , so the total solution
is
, so the total solution
is
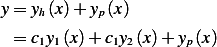
To solve the homogeneous ODE
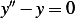
Assume the solution is 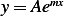 , hence the characteristic equation is
, hence the characteristic equation is 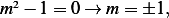 hence the
solution is
hence the
solution is 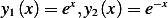 , so
, so
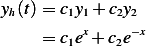
Or the solution can be written in hyperbolic sin and cosine
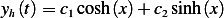
Now to find particular solution, use variation of parameters. Assume
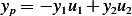
where
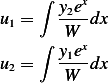
Where
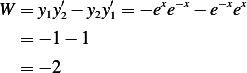
Hence
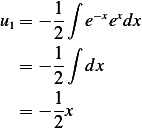
and
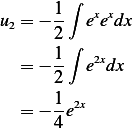
Hence the solution is
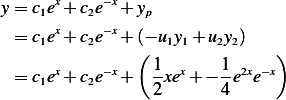
Hence
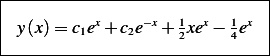
problem: Show that the minimal area of a surface of revolution in a catenoid, that is, the surface found by revolving a catenary
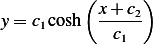
about the  axis
axis
solution:
First we assume that 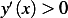 over the integration range. And that the lower end of the integration
over the integration range. And that the lower end of the integration  is smaller than the upper limit
is smaller than the upper limit 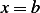
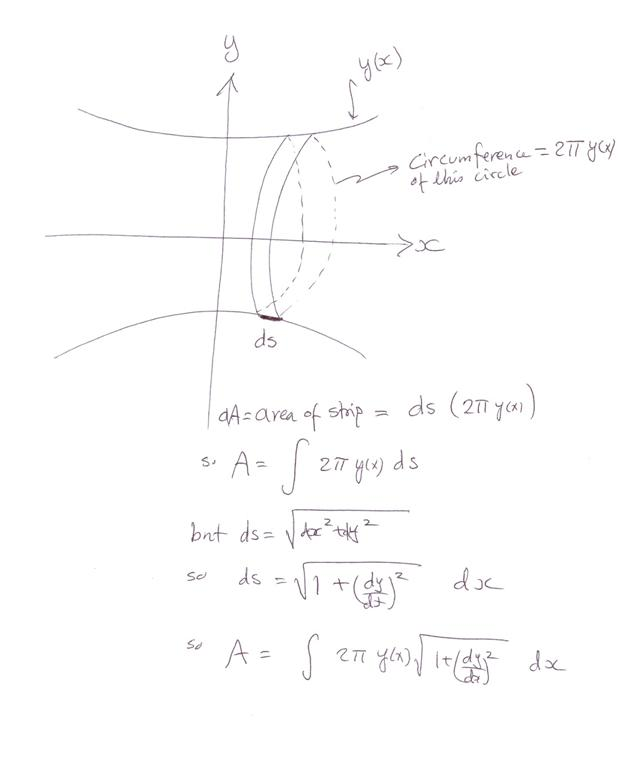
If we view a small 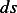 at
at 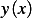 we see that it has a length of
we see that it has a length of
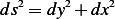
Hence
or we can also write
So there are 2 ways to solve this depending if we use (1) or (2). Let us leave the choice open for a little longer.
Now a size of a differential area 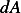 of a strip of width
of a strip of width 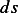 and a length given by the circumference of the
circle generated by rotation is
and a length given by the circumference of the
circle generated by rotation is
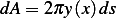
Hence the total surface area is the integral of the above over the range which 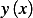 is defined at. Let this be
from
is defined at. Let this be
from 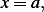 to
to 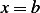 is given by
is given by
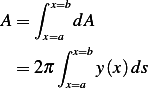
Since we have 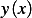 already in the Lagrangian, let then pick expression (2) from the above.
already in the Lagrangian, let then pick expression (2) from the above.
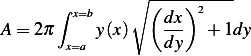
Now I need to change the limits. Let 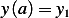 , and let
, and let 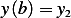 hence
hence
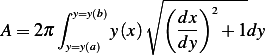
If we write the above in the more standard format, we have
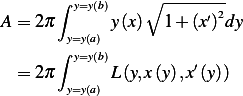
Remember now that 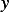 is the independent variable, and
is the independent variable, and 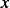 is the dependent variable. This is different from
the normal way.
is the dependent variable. This is different from
the normal way.
Hence the Lagrangian 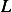 is
is
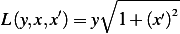 | (3) |
If I had picked expression (1) instead, I would have obtained the Lagrangian as
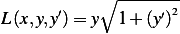 | (4) |
Both will give the same answer but with (3) we have 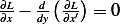 and the first term
and the first term 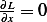 since
since 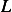 does not depend on
does not depend on 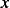 , and now we can just say that
, and now we can just say that 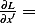 constant,. While with (4) we have
constant,. While with (4) we have 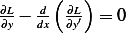 now
now 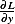 is not zero.
is not zero.
Now we continue, and we will use (3) as our lagrangian.
We start the solution of the problem. We seek a function 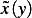 which minimizes
which minimizes 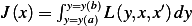 .
.
Where 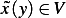 s.t.
s.t. ![C2[a,b ]](ma87x.png) , and let the set of admissible functions
, and let the set of admissible functions
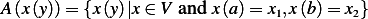 ,
,
and let the set of admissible directions 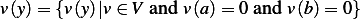
Now that we have written down all the formal definitions, we can just solve this by applying
Euler-Lagrange equation since the Lagrangian above meets the conditions of using Euler-Lagrange equations
(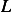 is a function of
is a function of 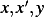 and
and 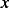 is defined at the boundary conditions with a dirichlet type boundary
conditions).
is defined at the boundary conditions with a dirichlet type boundary
conditions).
The Euler Lagrangian equation is
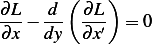
Since 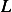 does NOT depend on
does NOT depend on 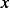 then
then 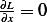 , and the above reduces to
, and the above reduces to
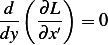
Since the derivative is zero, then we can write that
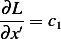
Where 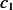 is some constant. So the above becomes
is some constant. So the above becomes
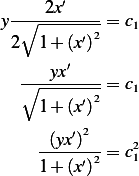
Hence we have
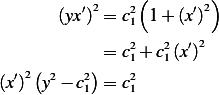
Hence the final ODE is
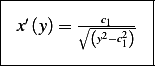
This is a linear ODE Its solution is found by integration both side as follows
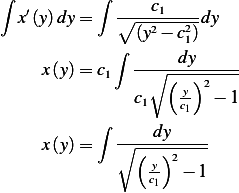
Let 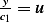 hence
hence 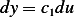 and the above becomes (do not need to worry about limits of integrations, as I
will flip back the earlier variable in a minute)
and the above becomes (do not need to worry about limits of integrations, as I
will flip back the earlier variable in a minute)
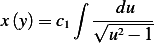
Which from table is given by
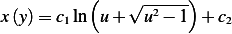
Where 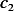 is constant of integration. Hence going back to our variables, we have
is constant of integration. Hence going back to our variables, we have
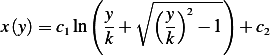 | (3) |
From tables I found that 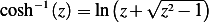
Hence (3) can now be written as
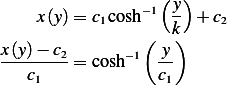
Or
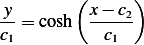
Then
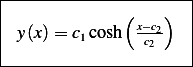
So the above curve will minimize the surface area.
Problem 1 (section 3.3,#14, page 177)

answer:
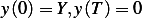
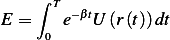
but
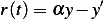
Hence
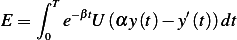
Hence the Lagrangian is
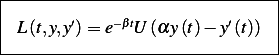
since 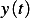 is defined at boundaries of the interval, we can use Euler-Lagrange equations
is defined at boundaries of the interval, we can use Euler-Lagrange equations
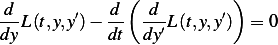
Now the first term above is
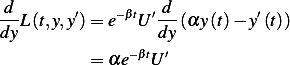
and the second term is
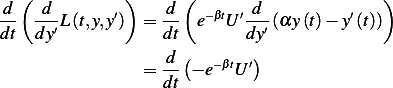
Hence our E-L equations now looks like
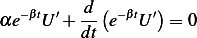 | (1) |
Since 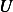 is a function of
is a function of  , then
, then
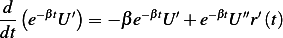
And (1) now becomes
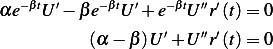
This is separable ODE, hence
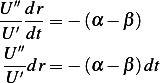
Integrate both sides
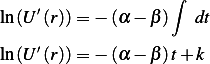
where 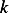 is constant on integration
is constant on integration
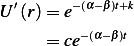
where 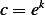 is another constant
is another constant
But 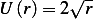 hence
hence 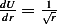 and the above becomes
and the above becomes
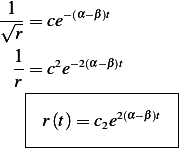
Where since 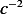 is constant, I call it
is constant, I call it 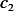
Now, Since
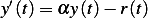
Then
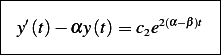
The solution is
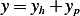
Assume 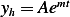 , hence
, hence 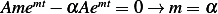
So the solution is
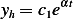
For the particular solution, guess a solution. Since the forcing function is of the form 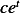 ,
guess
,
guess
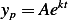
so 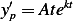 and we substitute this solution in the ODE above, we obtain
and we substitute this solution in the ODE above, we obtain
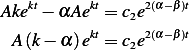
so by comparing exponents, we see that 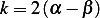 and
and 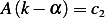 hence
hence 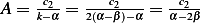
Therefore
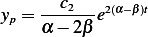
Hence, since
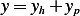
Then
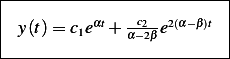
We now find 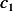 and
and 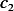 from I.C. At
from I.C. At 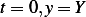 , hence
, hence
at 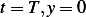 , hence
, hence
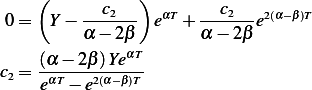
so from (2)
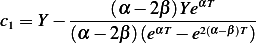
Hence
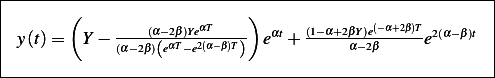
and
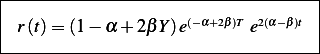
Analysis on results:
These are 3 plots showing 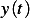 and
and 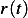 . The first is for
. The first is for 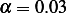

This one is for 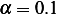

We notice that the higher the interest rate 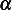 is the more capital will accumulate, which means to achieve
the goal of zero capital at death the rate
is the more capital will accumulate, which means to achieve
the goal of zero capital at death the rate 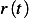 is more steep near the end. If the money hardly accumulate
during life time, i.e. when the interest rate is very low, then we should expect a straight line for
is more steep near the end. If the money hardly accumulate
during life time, i.e. when the interest rate is very low, then we should expect a straight line for 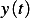 , which is
verified by this plot below when I set
, which is
verified by this plot below when I set