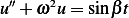 ,
, 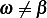
problem: Find the general solution of the following differential equations
(m) 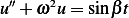 ,
, 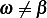
solution:
We start by assuming 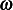 is real, hence
is real, hence 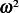 must be positive.
must be positive.
Now, the general solution is
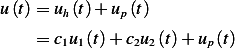
Where 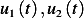 are the 2 independent solutions of the homogeneous differential equation
are the 2 independent solutions of the homogeneous differential equation
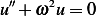
and 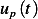 is the particular solution.
is the particular solution.
To find 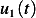 and
and 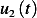 , we assume the homogeneous solution is
, we assume the homogeneous solution is 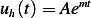 for some
constants
for some
constants 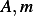 and substitute this assumed solution in the ODE. We obtain the characteristic
equation
and substitute this assumed solution in the ODE. We obtain the characteristic
equation 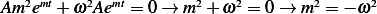 or
or 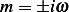 , hence
, hence 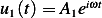 and
and
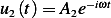 .
.
Since the homogeneous solution is a linear combination of all the independent solutions, we take the sum
and the difference of these solutions, and using Euler relation which converts the complex exponential to the
trigonometric 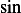 and
and 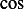 functions we obtain
functions we obtain
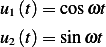
and we now write
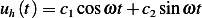
Now to obtain 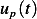 , we use the method of undetermined coefficients. Assume
, we use the method of undetermined coefficients. Assume
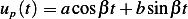
and plug into the original ODE, we obtain
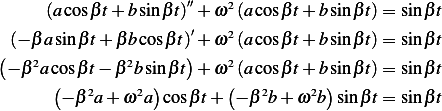
Hence by comparing coefficients we obtain
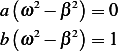
Since 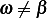 (given), then
(given), then 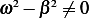 , hence this must mean the following
, hence this must mean the following
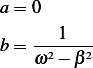
Therefor, the particular solution now can be written as
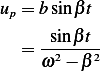
Hence the general solution, which is 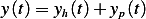 is given by
is given by
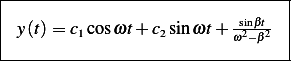
Where 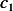 and
and 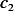 are constants that can be found from the initial conditions.
are constants that can be found from the initial conditions.
problem: Find the general solution of the following differential equations
(n) 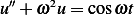
solution:
First, let the forcing function be called 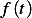 , hence
, hence 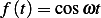 in this example.
in this example.
From (m) we found the homogeneous solution to be 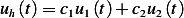 where
where
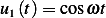
and
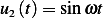
Now to find the particular solution we can not use the method of undetermined coefficients since the
forcing frequency is the same as the undamped natural frequency of the system  and this will lead to the
denominator going to zero. Hence use the method of variation of parameters which is a general method to find
particular solution which will work with this case.
and this will lead to the
denominator going to zero. Hence use the method of variation of parameters which is a general method to find
particular solution which will work with this case.
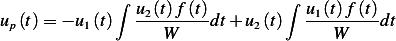
Where 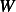 is the Wronskian of
is the Wronskian of 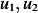 given by
given by 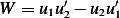
Hence 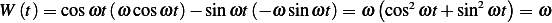
Hence
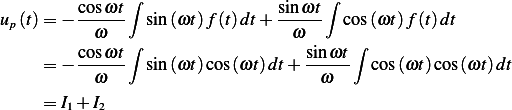
We now evaluate 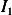 and
and 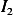 . Start with the easy one,
. Start with the easy one, 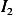
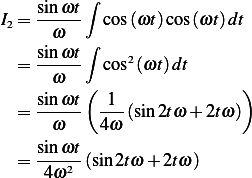
and now 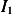
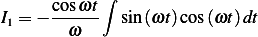
We can use integration by parts (do it twice) or use an trigonometric identity. From tables, Using the formula of
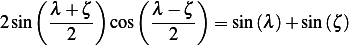
so if we let 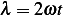 and
and 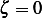 we obtain the integrand above, hence
we obtain the integrand above, hence
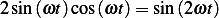
Substitute into 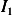
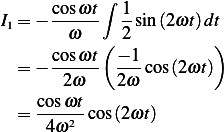
Therefor
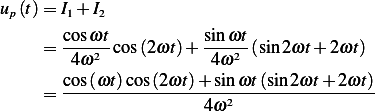
Hence the general solution is
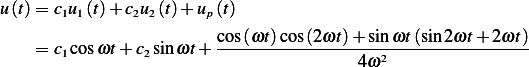
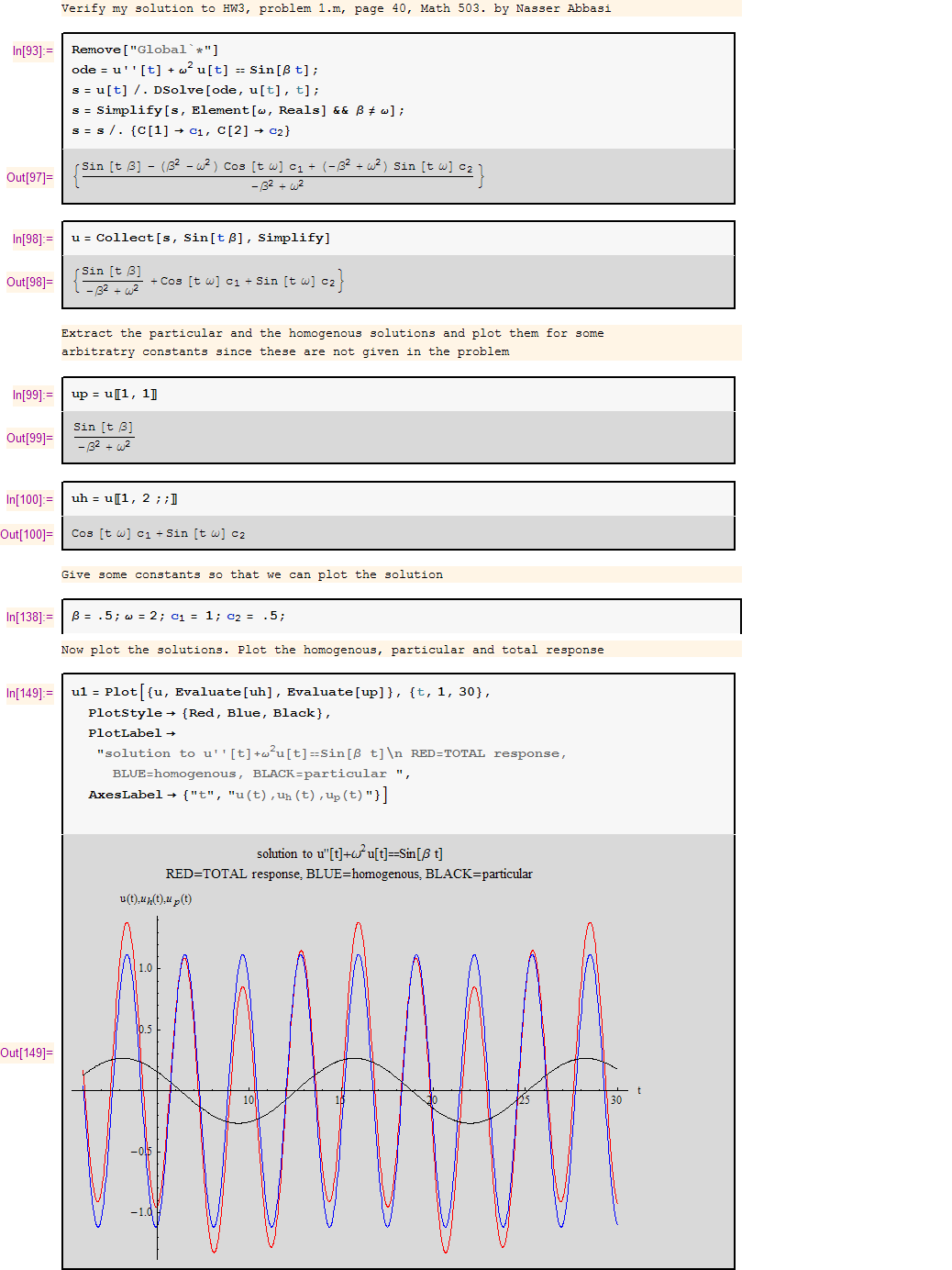
Verify using Mathematica
