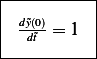problem:

solution:
Let ![[Θ ]](ma2x.png) be the dimension of temperature.
be the dimension of temperature.
A small note on how to scale the dependent variable and the independent variable in the problem.
For the dependent variable, say 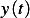 , if the problem does not say which problem parameters to scale
against, then look for a parameter or a combination of these parameters with the appropriate dimension of that
of the dependent variable such the parameter is the largest value. This way we are measuring the depndent
variable relative to the largest parameter in the problem. Hence when we write
, if the problem does not say which problem parameters to scale
against, then look for a parameter or a combination of these parameters with the appropriate dimension of that
of the dependent variable such the parameter is the largest value. This way we are measuring the depndent
variable relative to the largest parameter in the problem. Hence when we write 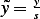 where
where  is the largest
parameter in the problem with dimension of
is the largest
parameter in the problem with dimension of 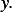
For the indepenent variable (typically this will be time), we look for the larget rate of change in the
problem involving this variable, and scale the time relative to this rate. Hence we write 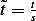 where now
where now  is
the smallest parameter in the problem with dimension of
is
the smallest parameter in the problem with dimension of 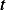 .
.
Now we start with the solution of the problem.
(a) 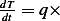 number
number hence
hence
![[ ]
Θ-
[q ]= T](ma12x.png)
i.e. the dimension of 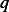 is temperature over time.
is temperature over time.
Now to find the dimension of 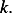 since
since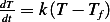 , then
, then ![[Θ]
T = [k][Θ]](ma16x.png) hence
hence
![[1 ]
[k]= T-](ma17x.png)
Now to find the dimension of 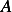 . Since
. Since 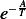 must be a numerical dimensionless value, then
must be a numerical dimensionless value, then 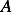 must have
the same dimensions as
must have
the same dimensions as 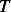 (which has dimension
(which has dimension ![[Θ]](ma22x.png) ), hence
), hence
![[A]= [Θ ]](ma23x.png)
(b) The constants in this problem are 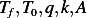 , and the dependent variable is
, and the dependent variable is 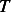 which is the
temperature of the sample, and the independent variable is
which is the
temperature of the sample, and the independent variable is 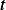 which is time.
which is time.
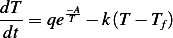
Hence to reduce the above ODE to dimensionless form, we need to transform the dependent and the
independent variables to dimensionless variables. Start with the dependent variable 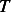 .
.
We write 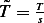 , so we need to find
, so we need to find  as a combination using the constants
as a combination using the constants 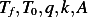 in the ODE
which would have the dimension of temperature to make
in the ODE
which would have the dimension of temperature to make 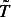 dimensionless.
dimensionless.
This is easy, since we are told to use 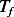 , hence
, hence 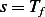 and so
and so
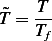 | (1) |
Now we need to transform the independent variable, which is time  , hence we write
, hence we write 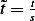 ,
and we need to find
,
and we need to find  as a combination of the constants
as a combination of the constants  which has a dimension of
time.
which has a dimension of
time.
Looking above at the dimensions of these constants, we see that the following combinations are possible:
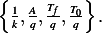 Now since we want the new time scale to be large when the heat loss is large, and since the heat
loss is proportional to
Now since we want the new time scale to be large when the heat loss is large, and since the heat
loss is proportional to 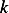 , hence we pick
, hence we pick 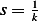 , this will make
, this will make  small and
small and  will then be large.
Therefor
will then be large.
Therefor
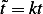 | (2) |
Now we convert the ODE to non dimensional using (1) and (2)
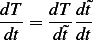
but from (2) we have 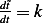 , hence
, hence
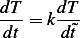
and since 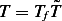 , then the above becomes
, then the above becomes
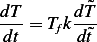
Hence the ODE 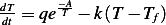 becomes (after replacing
becomes (after replacing 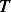 by
by 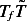 in the RHS)
in the RHS)
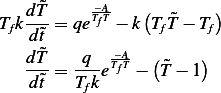
Now 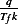 must be dimensionless. Verify
must be dimensionless. Verify ![-[ΘT]-
[Θ][1T] = 1](ma56x.png) . OK, so the above ODE can be written
as
. OK, so the above ODE can be written
as
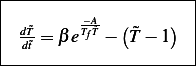
where 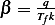
Note 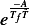 must be dimensionless also, since
must be dimensionless also, since 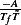 is dimensionless.
is dimensionless.
For the initial conditions, now it becomes 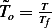
problem:

solution:
First draw a free body diagram. Assume the ball is moving upwards, and assume the drag force is
given by 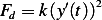 where
where 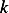 is constant of proportionality, and weight of ball is given by
is constant of proportionality, and weight of ball is given by
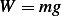
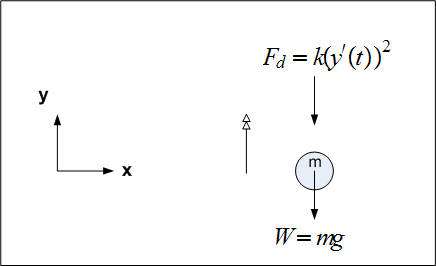
Now to obtain the equation of motion, apply Newtons second law 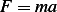 , hence we obtain
, hence we obtain
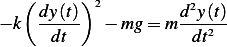
Notice that we assumed the positive  direction is upwards. Hence we obtain the equation of
motion
direction is upwards. Hence we obtain the equation of
motion
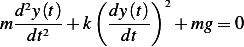
with the initial conditions
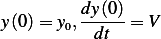
This problem has the following constants: 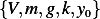 . To find the dimensions of
. To find the dimensions of 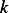 , since
, since 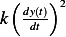 must have the dimension of Newton
must have the dimension of Newton ![[N]](ma73x.png) then we write
then we write
![[ ( ) ]
dy(t) 2 [ L-] [L]2
[N ]= k dt → M T2 = [k] T](ma74x.png)
![[ ]
M
[k]= L-](ma75x.png)
and ![[ L]
[g]= T2](ma76x.png) , and
, and ![[m ]= [M ]](ma77x.png) , and
, and ![[ L]
[V]= T](ma78x.png) , and
, and ![y0 = [L]](ma79x.png) , hence we write
, hence we write
![{ [L ] [ L ] [M ] }
constants → V = -- ,m = [M],g = -2- ,k = -- ,y0 = [L ]
T T L](ma80x.png)
Now we can start scaling the ODE.
The dependent variable is 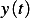 , and the independent variable is
, and the independent variable is 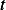 . Hence we write
. Hence we write 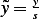 , where
, where
![[s]= [L]](ma84x.png) , so using the above constants, we need to find a combination which has the dimension of length
, so using the above constants, we need to find a combination which has the dimension of length ![[L ]](ma85x.png) .
Clearly
.
Clearly 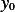 is one possibility. There are other combinations which give the dimension of length. We find the
following:
is one possibility. There are other combinations which give the dimension of length. We find the
following: 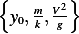 .
.
Now we get to the hard part of these scaling problems. Which combination to choose? The problem did not
give us a hint on this. I choose 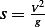 , therefor
, therefor
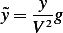
Now for the time scale. We write 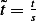 where
where ![[s]= [T]](ma91x.png) , looking at the above constants, we
need a combination with dimension
, looking at the above constants, we
need a combination with dimension ![[T]](ma92x.png) , we see that
, we see that 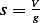 has the dimension of time, so we
have
has the dimension of time, so we
have
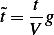
Now that we have the scaling completed, we apply them to scale the ODE. In otherwords, we need to
rewrite the ODE so that instead of using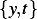 it will use
it will use 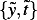
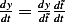 , but
, but 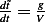 , hence
, hence
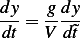
and 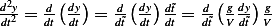 hence
hence
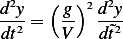
Hence the scaled ODE is
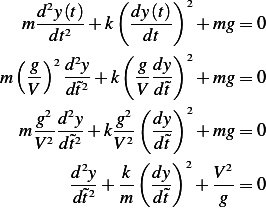
Now replace 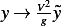
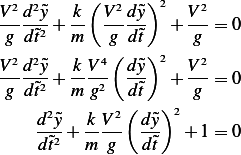
Lets us now verify the above is dimensionless. Looking at ![[ ] [ ] [ ][ ]
-kV2 → [M][-1][L]2 -1L → [M][-1] L22 T2
m g L M T T2- L M T L](ma105x.png)
Hence ![[-kV2]→ 1
m g](ma106x.png) (like magic)
(like magic)
So the dimensionless ODE is
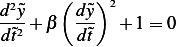
where 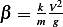
Now for the initial conditions in terms of the new scaled variables. Since
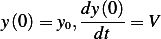
hence
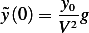
and 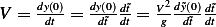 , but
, but 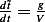 hence
hence
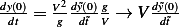
So 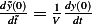 , but
, but 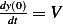 , therefor
, therefor
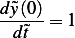
So the equation of motion in scaled dimensionless form is
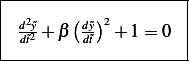
with initial conditions
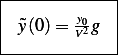
and