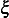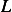 defined by
defined by 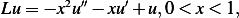 such that
such that
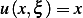 for
for 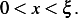
problem:
Find fundamental solution associated with operator 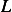 defined by
defined by 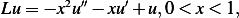 such that
such that
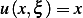 for
for 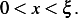
answer:
The fundamental solution can be written as
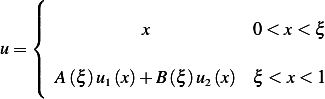
And our goal is to determine 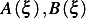 . In the above
. In the above 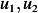 are the 2 independent solution to the
homogenous equation
are the 2 independent solution to the
homogenous equation 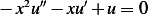
We start by finding 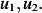 We try solution
We try solution 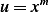 and substitute this into the above homogenous equation,
we obtain the characteristic equation
and substitute this into the above homogenous equation,
we obtain the characteristic equation 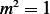 , hence
, hence 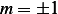 the 2 solution are
the 2 solution are 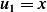 and
and 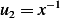 . Hence
our fundamental solution now looks like
. Hence
our fundamental solution now looks like
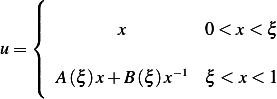
Now consider the test function  , hence
, hence
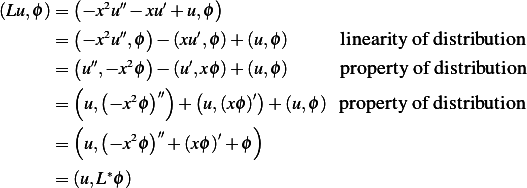
Where 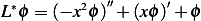
Hence expanding the differentiation in the above and simplifying we obtain
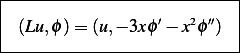
Now take 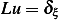 , i.e. put a point source as input, then we are looking for
, i.e. put a point source as input, then we are looking for 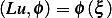 from the
properties of delta function. In other words, we are looking for
from the
properties of delta function. In other words, we are looking for
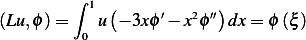
Hence
Looking at the first integral, and perform integration by parts. In these calculations we note that
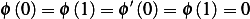
Hence
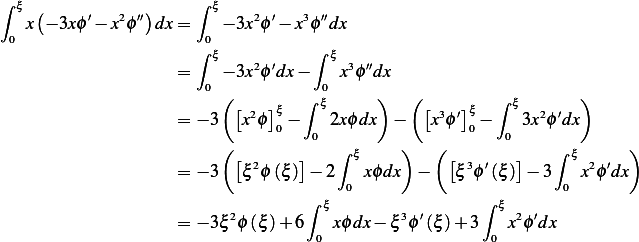
Now do integration by part on the last integral above
Now looking at (1) above, we now do integration by part on 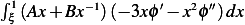
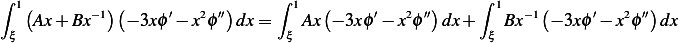
Consider the first integral above in the RHS, we write
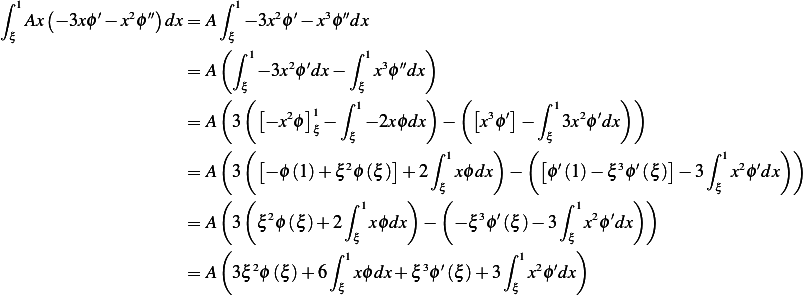
Now do integration by part on the last term in the above line
Now we do integration by parts on 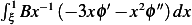
Hence, from (2),(3),(4),(5), we have
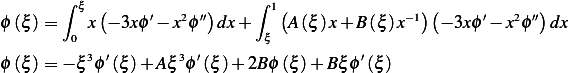
or
![[ ]
ϕ (ξ )= ϕ (ξ )(2B)+ ϕ′(ξ) − ξ3+ Aξ3+ B ξ](ma35x.png) | (6) |
By looking at the coefficients on 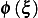 , and compare, we see that
, and compare, we see that 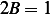 or
or
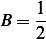
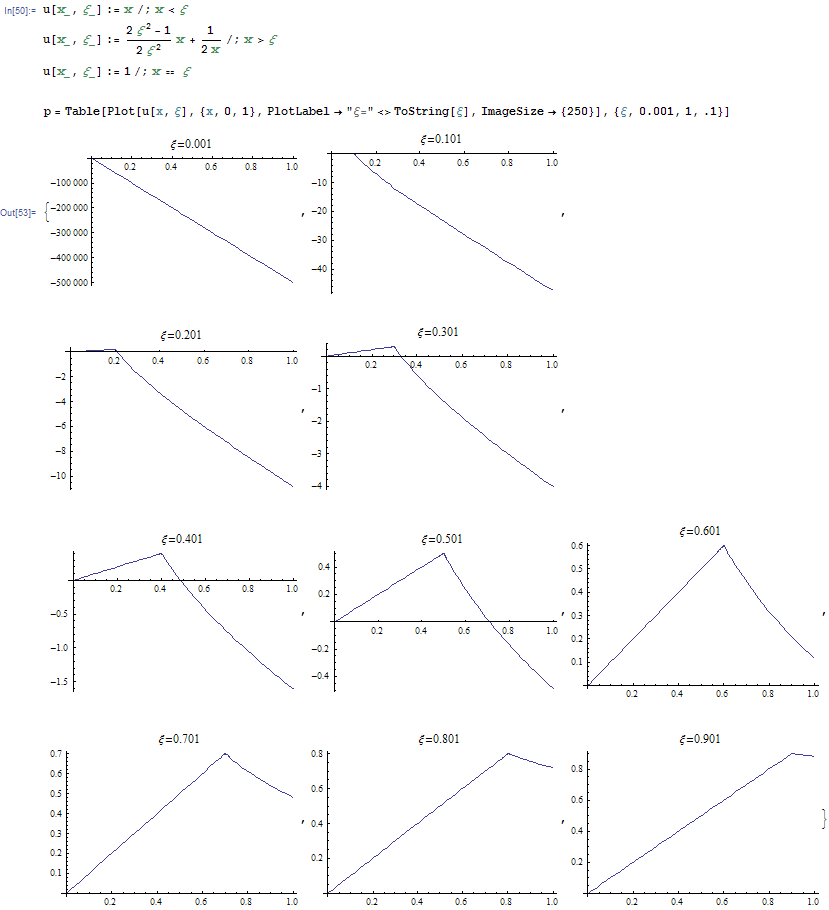
We can now use the continuity condition at 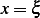 and write
and write
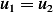 at
at 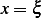 , hence
, hence
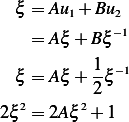
Hence
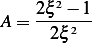
Therefor the fundamental solution is
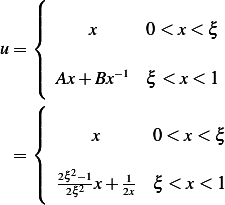
Here is a plot for few values of