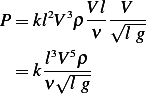problem:

solution:
The blast equation is given by
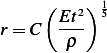
Where  is radius of blast in meters,
is radius of blast in meters, 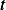 is time since explosion in seconds,
is time since explosion in seconds, 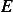 energy of explosion in
Joules,
energy of explosion in
Joules, 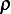 is air density in Kg/m^3
is air density in Kg/m^3
We are given 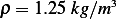 and
and 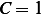 , hence the above can be rewritten as
, hence the above can be rewritten as
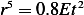
Let 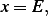
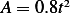 ,
, 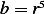 , then we have
, then we have
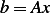
And now 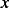 is found by least squares solution. Once
is found by least squares solution. Once 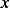 is found, then
is found, then 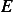 is found since
is found since
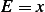 .
.
The code is shown on the next page. The least squares solutions shows that



problem:

solution:
First make a list of all the physical variables and the corresponding dimensions.
| Variable | 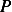 (power) (power) |  (ship length) (ship length) | 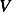 | 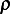 | 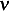 | 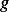 |
| meaning | work rate(F*d/t) | in meters | ship speed | water density | water Viscosity | gravity |
| Dimension | 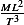 | 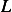 | 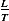 | 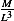 | 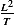 | 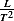 |
Hence we seek a physical law of the form
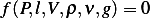
The function 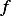 is a combination of all the physical variables. Hence we write
is a combination of all the physical variables. Hence we write
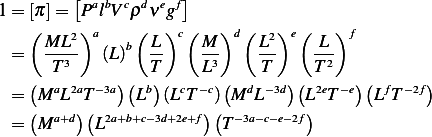
For the above combination to be dimensionless, we must have each exponent term equal to zero. Hence we obtain the following 3 equations
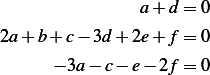
Writing the above in matrix form
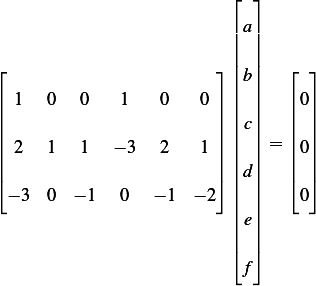
We see that the dimension matrix 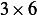 , hence its row space has dimension
, hence its row space has dimension 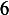 and its column space has
dimension
and its column space has
dimension 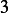 . We need now to find the basis for the Null Space of the dimension matrix. Now reduce
. We need now to find the basis for the Null Space of the dimension matrix. Now reduce 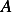 to its
reduce row echelon form
to its
reduce row echelon form

Now multiply last row by  , and now subtract last row from second
row
, and now subtract last row from second
row
 and this is the final reduce row echelon form
and this is the final reduce row echelon form
we have rank=3 (the first 3 columns are Linearly independent). Therefor, we use the first 3 variables as the
pivot variables, which are 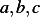 and use as the free variables those which correspond to the last 3 columns,
which are
and use as the free variables those which correspond to the last 3 columns,
which are 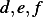
Now since
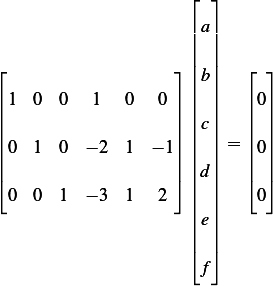
By back substitution, from the 3rd row we obtain 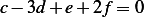 , or
, or 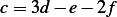 and from the
second row we obtain
and from the
second row we obtain 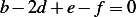 , or
, or 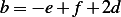 , and from the first row we obtain
, and from the first row we obtain 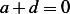 or
or
Hence the solution now can be written in terms of the free variables as
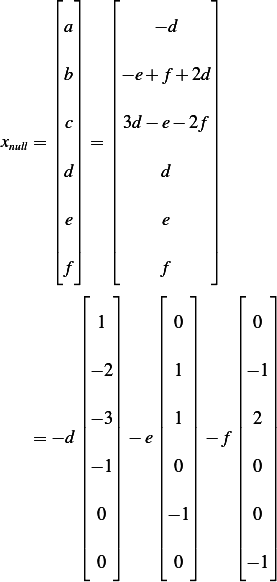
Therefor the basis for the null space of  are
are
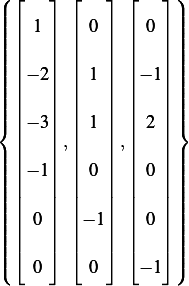
Hence
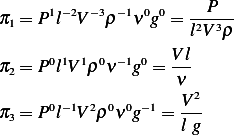
Hence the complete set is
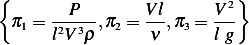
Hence the general solution is 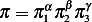
The Pi theorem says that there is a physical law expressed in terms of the dimensionless quantities called
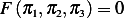 corresponding to the physical law
corresponding to the physical law 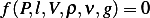
Now, we need to solve for 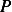 , hence we write
, hence we write
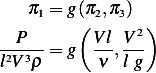
Hence if we let 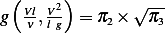 , then we see that
, then we see that
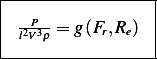
where
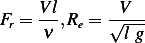
Let 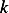 be some constant, then the power needed is given by
be some constant, then the power needed is given by