Answer:

Given:

1.: $Ri ,$ Event that it rains on day $i$
2.: $Rci$ ,Event that it does not rain on day $i$
3.: $P (R0) = p,$ Probability of rain on day $0$
4.: $P (R |R ) = α i i−1$ ,Probability of rain on day $i$ given it rained on day $i − 1$
5.: $( c c ) P R i|R i− 1 = β$ ,Probability of no rain on day $i$ given it did not rain on day $i − 1$
6.: Only today's weather is relevant to predicting tomorrow rain

Find:

Probability of rain in $n$ days and what happen as $n → ∞$

Solution:

Consider the experiment that generates today's weather. Hence possible outcomes can be divided into 2 disjoint events: rain and no rain (A day can either be rainy or not, hence this division contains all possible outcomes).

Hence

Ω = {R ,Rc } 0 0

Now using the law of total probability, we write

P (R1) = P (R1 |R0 )P (R0 ) + P (R1 |Rc0)P (Rc0)

(1)

But

Note: To proof the above, we can utilize a simple state transition diagram as follows

Now, substitute (2) into (1) and given that $P (R1 |R0 ) = α$ and $P (R0) = p$ and $P (Rc0) = 1 − p$ , then (1) becomes

P (R1) = αp + (1 − β )(1 − p)

(3)

Now we can recursively apply the above to ﬁnd probability of rain on the day after tomorrow. Let $R0 → R1$ and $R1 → R2$ , hence the above (1) becomes

P (R2) = P (R2 |R1 )P (R1 ) + P (R2 |Rc1)P (Rc1)

(4)

Now using (3) for $P (R1 ),$ and given that $P (R2 |R1 ) = α$ (This probability does not change, since we are told only today's weather is relevant), and given that $c P (R 1) = (1 − P (R1 ))$ and that $c P (R2|R 1) = (1 − β )$ , then (4) becomes

We see that as we continue with the above process, terms will be generated with the form (something) $× αm$ and (something) $× βr$ , where the powers $m, r$ are getting larger and larger as $n$ gets larger. But since $α,β < 1$ , hence all these terms go to zero. So we only need to look at the terms which do not contain a product of $′ α s$ and product of $′ β s$

Hence the above reduces

P (R2) ≈ p (1 − 2 α − 2β + 2α β) + α + β − αβ

There is a pattern here, to see it more clearly, I generated more $P (R ) i$ for $i = 3,4, 5,6,7$ using a small piece of code and removed all terms of higher powers of $α, β$ as described above, and I get the following table

$i$	$P (Ri)$
$0$	$p$
$1$	$1 − β + p(− 1 + α + β)$
$2$	$α + β − α β + p(1 − 2α − 2β + 2αβ )$
$3$	$1 − α − 2β + 3 αβ + p (− 1 + 3α + 3β − 6αβ )$
$4$	$2α + 2β − 6α β + p (1 − 4α − 4β + 12α β)$
$5$	$1 − 2α − 3β + 10α β + p(− 1 + 5α + 5β − 20 αβ)$
$6$	$3α + 3β − 15αβ + p(1 − 6α − 6β + 30αβ )$

Hence the pattern can be seen as the following

Where $mod (n,2) = 0$ for even $n$ and $1$ for odd $n$ , and $⌊ ⌋ n2$ means to round to nearest lower integer and $⌈ ⌉ n 2$ means to round upper.

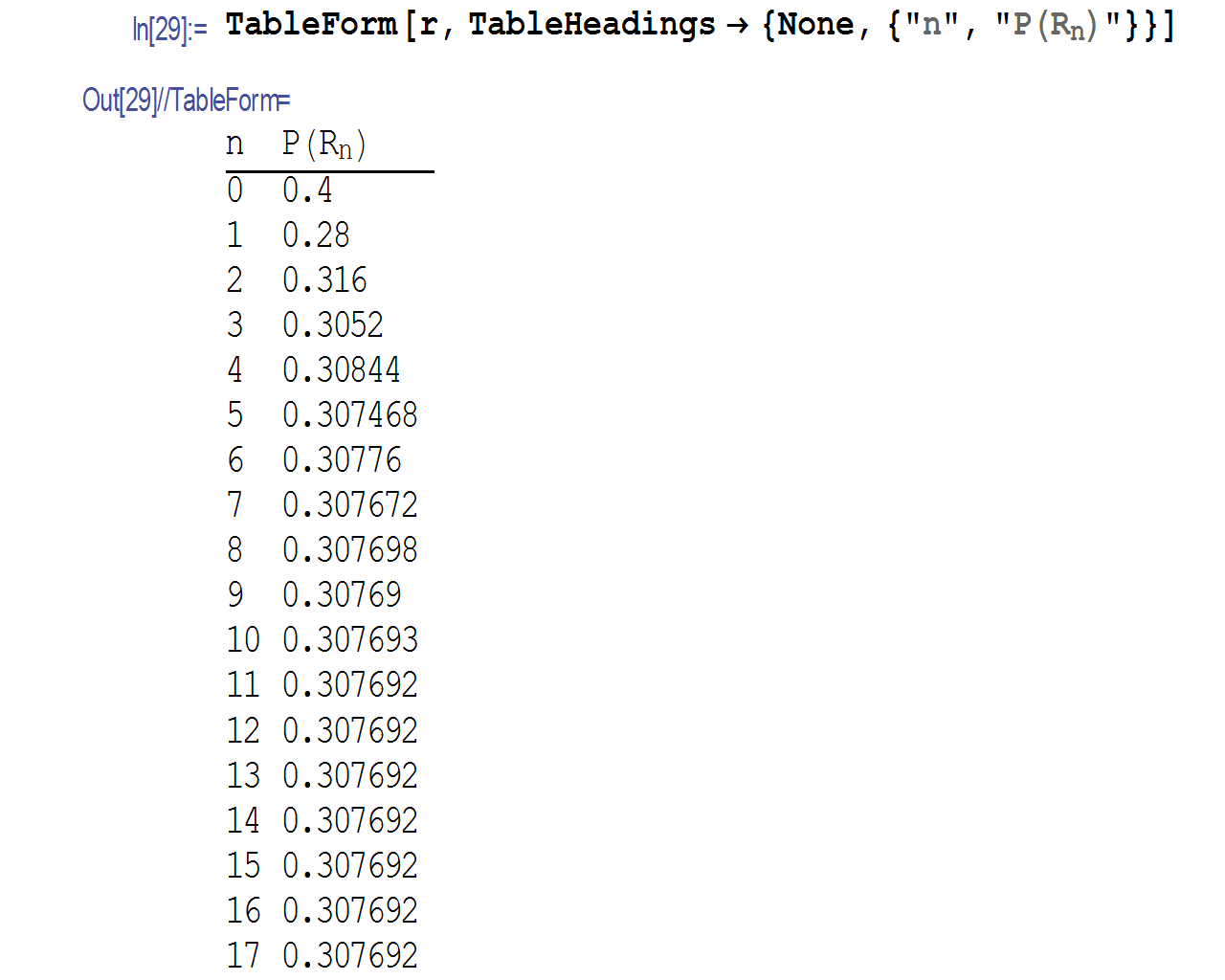
The above is valid for very large $n$ .

As $n → ∞$ $P (Rn )$ will reach a ﬁxed value (I ﬁrst though it will always go to 1, but that turned out not to be the case). I could not ﬁnd an exact expression for $P (Rn )$ as $n → ∞$ , but I wrote a small program which simulates the above, and generates a table. Here is a table for few values as $n$ gets large, these are all for $α = .3,β = .6,p = .4,$ notice that $P (Rn )$ ﬂuctuates up and down from one day to the next as it converges to its limit.

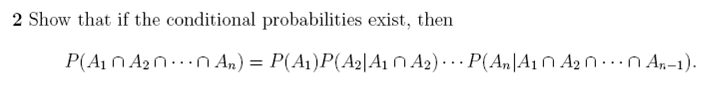
Given: Conditional probabilities exist

Show: $P (A1 ∩ A2 ∩ A3 ∩ ⋅ ⋅⋅An) = P (A1 ) + P (A2 |A1 ∩ A2) + ⋅⋅⋅ + P (An |A1 ∩ A2 ∩ ⋅⋅⋅ ∩ An −1)$

Solution:

Since Conditional probabilities exist, then we know that the following is true

P (X ∩ Y ) = P (X |Y )P (Y )

Let $X = An$ and $Y = A1 ∩ A2 ∩ A3 ∩ ⋅⋅⋅ ∩ An −1$ hence the above becomes

P (A1 ∩ A2 ∩ ⋅⋅⋅An ) = P (An|A1 ∩ A2 ∩ ⋅⋅⋅ ∩ An−1) P (A1 ∩ A2 ∩ ⋅⋅⋅ ∩ An −1)

Now apply the same idea to the last term above. In other words, we write

P (A1 ∩ A2 ∩ ⋅⋅⋅ ∩ An −1) = P (An− 1|A1 ∩ A2 ∩ ⋅⋅⋅ ∩ An− 2) P (A1 ∩ A2 ∩ ⋅⋅⋅ ∩ An −2)

We repeat the process until we obtain $P (A ∩ A ) = P (A |A )P (A ) 1 2 2 1 1$

Hence, putting all the above together, we write

The above is what is required to show (terms are just rewritten is reverse order from the problem statement, rearranging, we obtain

P (A1 ∩ A2 ∩ ⋅⋅⋅An ) = P (A1 )P (A2|A1 )⋅⋅⋅P (An −1|A1 ∩ A2 ∩ ⋅⋅⋅ ∩ An− 2)P (An |A1 ∩ A2 ∩ ⋅⋅⋅ ∩ An− 1)

QED

Given:

Axioms of probability:

1.: $P (Ω) = 1$
2.: if $A ⊂ Ω$ then $P (A) ≥ 0$
3.: if $A, B$ are disjoint events (i.e. $A ∩ B = ∅$ ) then $P (A1 ∪ A2 ∪ A3 ∪ ⋅⋅⋅ ∪ An ) = P (A1 ) + P (A2 ) + ⋅ ⋅⋅ + P (An )$

Show that $P (A ∪ B) ≤ P (A ) + P (B)$

Solution:

There are 4 possible cases.

1.: $A, B$ are disjoint
2.: $A ⊂ B$
3.: $B ⊂ A$
4.: $A, B$ have some common events between them. In other words $A ∩ B = C ⁄= ∅$

Case 1: If $A,B$ are disjoint then $A ∪ B = A + B$ by set theory. Now apply the probability operator on both sides we obtain that

P (A ∪ B ) = P (A + B )

Now, by Axiom 3, $P (A + B) = P (A ) + P (B)$ hence the above becomes

P (A ∪ B ) = P (A) + P (B )

Case 2: If $A ⊂ B$ then $A ∪ B = B$ by set theory. Now apply the probability operator on both sides we obtain that

P (A ∪ B ) = P (B )

But $P (B ) ≤ P (B ) + P (A )$ since $A ∈ Ω$ and so $P (A ) ≥ 0$ by axiom 2. Hence the above becomes

P (A ∪ B ) ≤ P (B ) + P (A )

(0)

Case 3: This is the same as case 2, just exchange $A$ and $B$

case 4: Since, by set theory

c A = A ∩ B + A ∩ B

Then apply Probability operator on both sides

P (A ) = P (A ∩ B + A ∩ Bc)

But by set theory $A ∩ B$ is disjoint from $A ∩ Bc$ , then by axiom 3 the above becomes

c P (A ) = P (A ∩ B ) + P (A ∩ B )

(1)

Similarly, by set theory

c B = B ∩ A + B ∩ A

Then apply Probability operator on both sides

c P (B ) = P (B ∩ A + B ∩ A )

But $B ∩ A$ is disjoint from $B ∩ Ac$ , by set theory, then by axiom 3 the above becomes

P (B ) = P (B ∩ A ) + P (B ∩ Ac)

(2)

Now by set theory

A ∪ B = A ∩ B + A ∩ Bc + B ∩ Ac

Apply the probability operator on the above

c c P (A ∪ B ) = P (A ∩ B + A ∩ B + B ∩ A )

But $A ∩ B, A ∩ Bc,$ and $B ∩ Ac$ are disjoint by set theory, then above can be written using axiom 3 as

c c P (A ∪ B) = P (A ∩ B) + P (A ∩ B ) + P (B ∩ A )

(3)

Add (1)+(2)

P (A ) + P (B ) = P (A ∩ B ) + P (A ∩ Bc ) + P (B ∩ A ) + P (B ∩ Ac )

subtract the above from (3)

Cancel terms (Arithmetic)

P (A ∪ B ) − [P (A ) + P (B)] = − P (B ∩ A )

or (algebra)

P (A ∪ B) = P (A ) + P (B) − P (B ∩ A)

Since $B ∩ A$ is an event in $Ω$ then $P (B ∩ A ) ≥ 0$ by axiom 2, hence the above can be written as

P (A ∪ B ) ≤ P (A) + P (B )

(4)

conclusion: We have looked at all 4 possible cases, and found that $P (A ∪ B) = P (A ) + P (B)$ or $P (A ∪ B ) ≤ P (A ) + P (B)$ , hence $P (A ∪ B ) ≤ P (A ) + P (B)$

Note: I tried, really tried, to ﬁnd a method which would require me to use the hint given in the problem that if $A ⊂ B$ , then $P (A) ≤ P (B )$ but I did not need to use such a relationship in the above. But I still show a proof for this identity below

Given: $A ⊂ B$ , Show $P (A) ≤ P (B )$

proof:

$c B = A ∪ A$ by set theory

$P (B) = P (A ∪ Ac)$ by applying probability to each side.

But $A, Ac$ are disjoint by set theory, hence $P (A ∪ Ac) = P (A ) + P (Ac )$ by axiom 3.

Hence $P (B ) = P (A) + P (Ac)$ , or $P (A ) = P (B ) − P (Ac)$

But by axiom 2, $c P (A ) ≥ 0$ , hence $P (A ) ≤ P (B )$ , QED

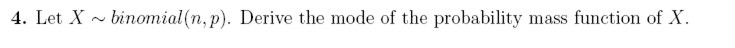
Given: $X$ binomial r.v., i.e. $( ) P (X = k ) = n pk (1 − p)n−k , k$ Find the mode. This is the value $k$ for which $P (X = k)$ is maximum

The mode is where $P (X )$ is maximum. Consider 2 terms, when $X = k$ , and $X = k − 1$ , hence $P (X )$ will be increasing when $PP((XX==kk−-)1) > 1$

But

( ) n P (X = k − 1) = p(k− 1)(1 − p )n− (k−1) k − 1

Hence

so $P (X )$ is getting larger when $(n−-k)-(1−p) k p > 1$ or

So as long as $k < p (1 + n )$ , pmf is increasing. Since $k$ is an integer, then we need the largest integer such that it is $< p(1 + n)$ , hence

k = ⌊p (1 + n )⌋

Given:

$P (D ) = 1 ∕1000$

members are aﬀected independently

Find: probability 2 individuals are aﬀected in population of size 100,000

part(a)

In Binomial random variable we ask: How many are infected in a trial of length $n$ given that the probability of being infected in each trial to be $p.$ Here we view each trial as testing an individual. Consider it a 'hit' if the individual is infected. The number of trials is $100,000$ , which is $n$ , and $p = 1 ∕1000$ .

Therefore, $X =$ how many are infected in population of 100000

Hence the probability of getting $k = 2$ hits is, using binomial r.v. is ( $k = 2$ in this case)

( ) n k n− k P (X = 2) = k p (1 − p )

or numerically

( ) 100000 2 100000−2 P (X = 2) = 0.001 (1 − 0.001) 2

(b)Using Poisson r.v. Poisson is a generalization of Binomial. X is the number of successes in inﬁnite number of trials, but with the probability of success in each one trial going to zero in such a way that $np = λ$ .We compute $p(X = k ) = λke−λ k!$ $,k = 0,1,2,....$

Hence here $X =$ how many are infected as $n$ gets very large and $p$ , the probability of infection in each individual goes very small in such a way to keep $np$ ﬁxed at a parameter $λ$ . Since here $n$ is large and $p$ is small, we approximate binomial to Poisson using $λ = np = 100000 × 0.001 = 100.0$

Hence

1002-− 100 p (X = 2) = 2! e

ps. computing a numerical value for the above, shows that using Binomial model, we obtain $P (X = 2)$

and using Poisson model

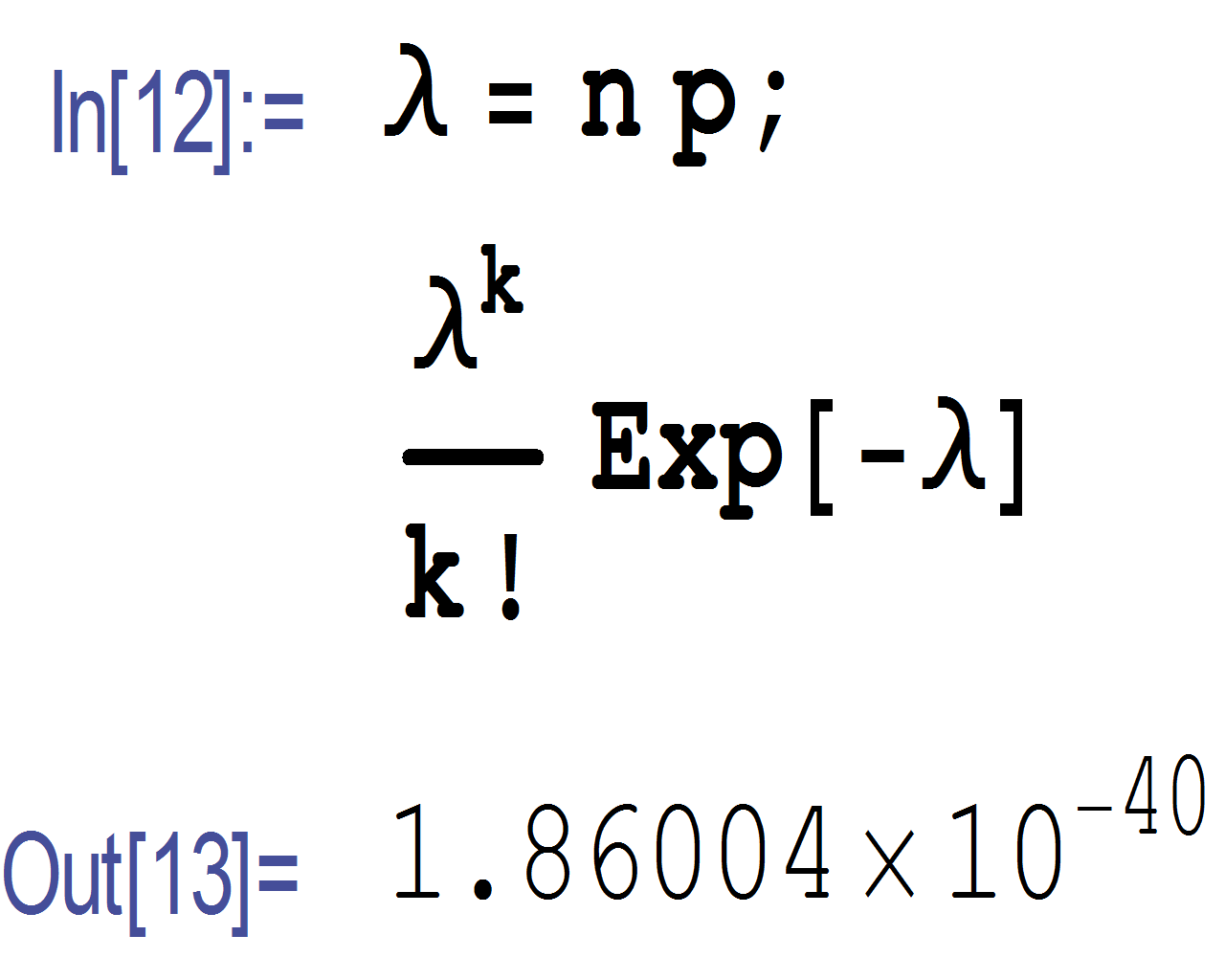
I am not sure, these are such small values, this means there is almost no chance of ﬁnding 2 individuals infected in a population of 100,000? I would have expected to see a much higher probability than the above. I do not see what I am doing wrong if anything.