HW 3.18

Nasser Abbasi

SOURCE CODE

% nma_HW_3_18 - Program to solve problem 3.18

clear all; help nma_HW_3_18; % Clear memory and print header

%

% by Nasser Abbasi

%

%* Set initial position and angle of the pendulum

alpha = input('Enter initial angle (degree):');

alpha = alpha*pi/180; % convert degree to radian

springRestLength=1; % rest length is 1 meter

ext = input('Enter extension from rest length: (m)');

pos = [alpha springRestLength+ext]

w0 = input('Enter initial angular velosity w (radian/sec):');

r0 = input('Enter initial mass velosity along the pendulum axis (m/s):');

v = [w0 r0];

state = [ pos(1) pos(2) v(1) v(2) ]; % Used by R-K routines

initialState = state;

%* Set physical parameters

param = struct('length',springRestLength, ...

'mass',0.1, ...

'k',0);

adaptErr = 1.e-3; % Error parameter used by adaptive Runge-Kutta

%* Loop over desired number of steps using specified

% numerical method.

nStep = input('Enter number of steps: ');

tau = input('Enter time step (sec): ');

% spring constants to try

springConstant=[10^2 10^3 10^4 10^5 10^6];

for i=1:length( springConstant )

param.k = springConstant(i);

time=0;

state = initialState;

for n=1:nStep

%* Record position for plotting

thetaPlot(n) = state(1);

rPlot(n) = state(2);

wPlot(n) = state(3);

speed(n) = state(4);

[state time tau] = rka(state,time,tau,adaptErr,'nma_HW_3_18_deriv',param);

end

averageTimeStep = time / nStep;

fprintf('Time used for k=%g is %g, average time step=%g\n',...

param.k,time,averageTimeStep);

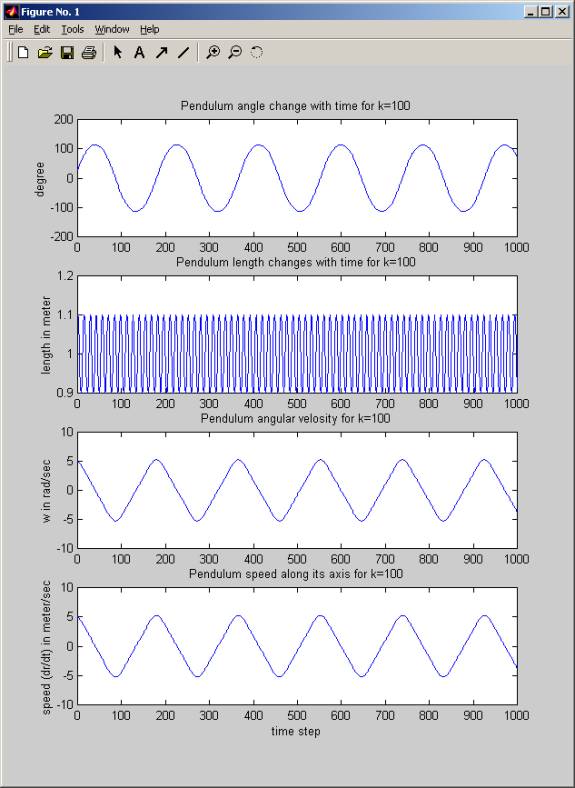
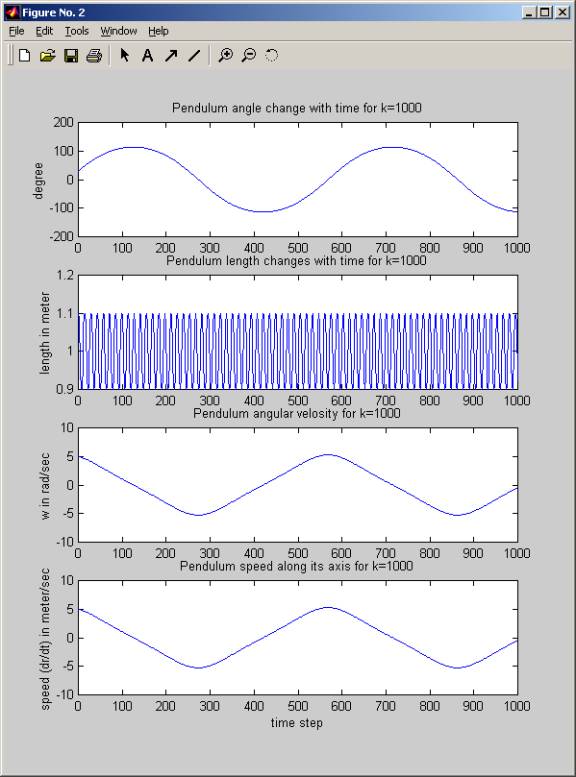
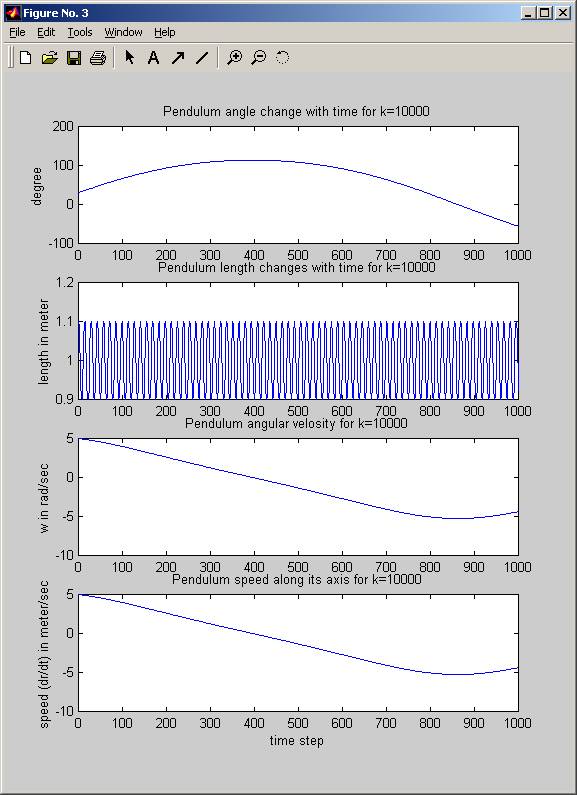
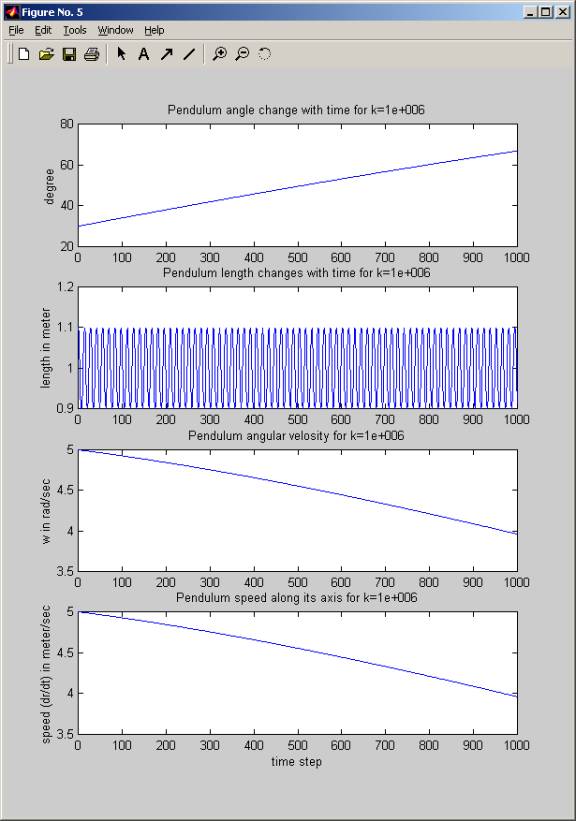
figure;

subplot(4,1,1);

plot( (180/pi) .* thetaPlot );

title(sprintf('Pendulum angle change with time for k=%g',param.k));

ylabel('degree');

subplot(4,1,2);

plot(rPlot);

title(sprintf('Pendulum length changes with time for k=%g',param.k));

ylabel('length in meter');

subplot(4,1,3);

plot(wPlot);

title(sprintf('Pendulum angular velosity for k=%g',param.k));

ylabel('w in rad/sec');

subplot(4,1,4);

plot(wPlot);

title(sprintf('Pendulum speed along its axis for k=%g',param.k));

ylabel('speed (dr/dt) in meter/sec');

xlabel('time step');

kTrack(i,1)=param.k;

kTrack(i,2)=averageTimeStep;

end

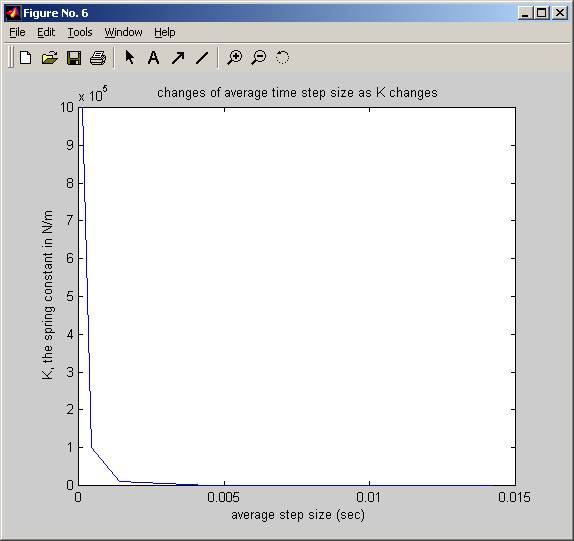
figure;

plot(kTrack(:,2),kTrack(:,1));

title(' changes of average time step size as K changes');

ylabel(' K, the spring constant in N/m');

xlabel(' average step size (sec)');

function deriv = nma_HW_3_18_deriv(s,t,param)

% Returns right-hand side of pendulum ODE; used by Runge-Kutta routines

% problem 3.18

%

% Inputs

% s State vector [theta r w speed]

% t

% param Parameter struct

% Output

% deriv Derivatives

% Nasser Abbasi, feb 20. 2002.

g= 9.8; % gravitation m/s^2

deriv(1) = s(3);

deriv(2) = s(4);

deriv(3) = -(g/s(2)) * sin(s(1));

deriv(4) = -(param.k/param.mass) * (s(2) - param.length);

return;

OUTPUT

» nma_HW_3_18

nma_HW_3_18 - Program to solve problem 3.18

Enter initial angle (degree):30

Enter extension from rest length: (m)0.1

pos =

0.5236 1.1000

Enter initial angular velosity w (radian/sec):5

Enter initial mass velosity along the pendulum axis (m/s):0.1

Enter number of steps: 1000

Enter time step (sec): 0.01

Time used for k=100 is 14.2045, average time step=0.0142045

Time used for k=1000 is 4.48814, average time step=0.00448814

Time used for k=10000 is 1.41925, average time step=0.00141925

Time used for k=100000 is 0.449157, average time step=0.000449157

Time used for k=1e+006 is 0.142036, average time step=0.000142036

»